- •Неопределённый интеграл
- •Интегрирование подстановкой
- •Определённый интеграл приложения определённого интеграла
- •Комплексные числа
- •Упражнения
- •Алгоритм перевод комплексного числа из алгебраической в тригонометрическую форму.
- •II. Комплексно-сопряженные числа.
- •III. Действия с комплексными числами в алгебраической форме.
- •IV. Действия с комплексными числами в тригонометрической форме.
- •V. Решение квадратных уравнений.
- •Модуль числа.
Определённый интеграл приложения определённого интеграла
1.Определенный
интеграл
 равен …
равен …
|
|
|
|
Решение:
Напоминаем,
что формула Ньютона – Лейбница имеет
вид
 В
нашем случае, используя формулу
В
нашем случае, используя формулу
![]() ,
имеем
,
имеем

2.Определенный
интеграл
 равен …
равен …
|
|
|
|

3.Скорость
движения тела задана уравнением
![]() .
Тогда путь, пройденный телом за время
от первой секунды до третьей секунды
движения, равен …
.
Тогда путь, пройденный телом за время
от первой секунды до третьей секунды
движения, равен …
Решение:
Напоминаем,
что путь
![]() ,
пройденный телом за отрезок времени от
,
пройденный телом за отрезок времени от
![]() до
до
![]() ,
движущимся прямолинейно со скоростью
,
движущимся прямолинейно со скоростью
![]() ,
вычисляется по формуле:
,
вычисляется по формуле:
 .
Тогда,
используя условие, имеем:
.
Тогда,
используя условие, имеем:

4.Площадь
фигуры, ограниченной графиком функции
![]() ,
прямыми
,
прямыми
![]() ,
,
![]() и
осью абсцисс, равна …
и
осью абсцисс, равна …
Решение:
Площадь
плоской фигуры вычисляется по формуле
 Тогда
получаем:
Тогда
получаем:
 Площадь
фигуры равна
Площадь
фигуры равна
![]() (кв. ед.).
(кв. ед.).
5.Площадь
фигуры, ограниченной графиком функции
![]() ,
прямыми
,
прямыми
![]() ,
,
![]() и
осью абсцисс, равна …
и
осью абсцисс, равна …
6.Определенный
интеграл
 равен …
равен …
Комплексные числа
Определение : Числа вида а + bi, где a и b - действительные числа, а i – мнимая единица называют комплексными числами. Число а называется действительной частью комплексного числа, bi - мнимой частью этого числа, b - коэффициентом мнимой части комплексного числа. Основное свойство числа i состоит в том, что i2= -1.
Запись z=a+bi называют алгебраической формой этого числа.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a φ |
|
|
|
|
|
|
|
0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим на комплексной плоскости точку z=a+bi, отличную от 0. Пусть луч Oz получается в результате поворота положительного луча Ox оси абсцисс на угол φ.
Тогда a=|z|cos φ, b=|z|sin φ. Поэтому число z можно записать так: z=|z|cos φ + i |z|sin φ = |z| ( cos φ + i sin φ ).
Обозначим |z| буквой r. Тогда z=r ( cos φ + i sin φ ). Запись комплексного числа в таком виде называют тригонометрической формой комплексного числа

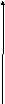 y
y
 z=a+bi
z=a+bi