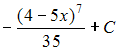- •Неопределённый интеграл
- •Интегрирование подстановкой
- •Определённый интеграл приложения определённого интеграла
- •Комплексные числа
- •Упражнения
- •Алгоритм перевод комплексного числа из алгебраической в тригонометрическую форму.
- •II. Комплексно-сопряженные числа.
- •III. Действия с комплексными числами в алгебраической форме.
- •IV. Действия с комплексными числами в тригонометрической форме.
- •V. Решение квадратных уравнений.
- •Модуль числа.
|
|
|
||||||||||||||||||
|
Производная
суммы двух функций:
Производная
произведения постоянной и функции:
Производная
произведения двух функций:
Производная
частного двух функций :
Производная
сложной функции:
Таблица производных основных элементарных функций:
Пример
:
1.Производная
функции
равна … 2.Производная
функции
равна … 3.Производная
функции
равна …
4.Производная
функции
1.Если
2.Если
3.Если
4.Если
5.Если
6.
Дана функция
7
.Угловой коэффициент касательной к
графику функции
4. Наибольшее и наименьшее значения функции на отрезке Наибольшее и наименьшее значения функция непрерывная на отрезке принимает на концах этого отрезка или в корнях производной функции, попавших в отрезок.
Пример
Найти
наибольшее
значение функции
Сравнивая
значения
1.Функция
2.Наименьшее
значение функции
3.Наименьшее
значение функции
4.Наибольшее
значение функции
5.Наименьшее
значение функции
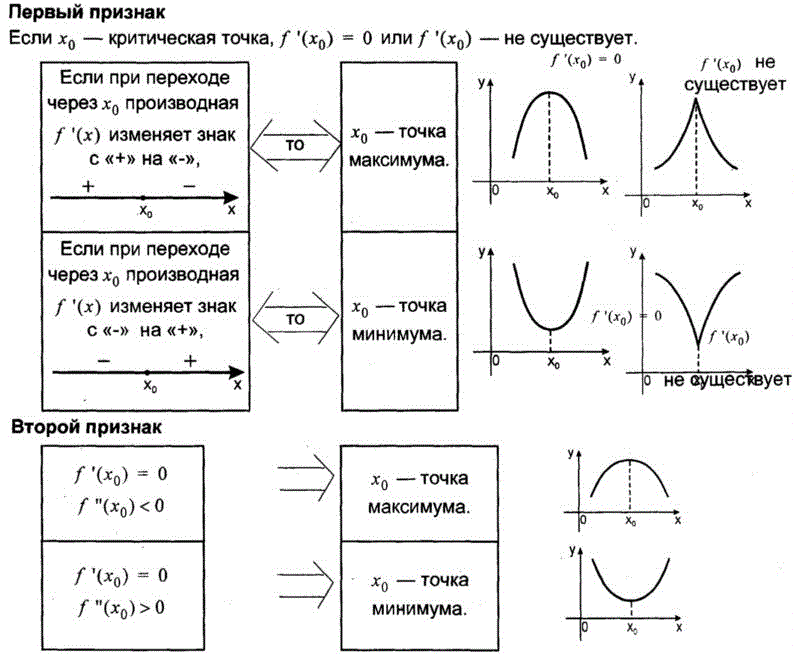
5. Экстремум функции
Для отыскания точек экстремума нужно найти точки, в которых производная равна нулю или не существует. Найти вторую производную и подставить в неё корни первой производной, определить знак результата и сделать вывод.
Для отыскания экстремума надо подставить точку экстремума в данную функцию и вычислить её значение.
Пример
1:
Пример
2:
Найти максимум и минимум функции
Вывод:
1.Для
функции
2.Для
функции
3.Для
функции
4.Для
функции
5.Для
функции
6.
Для функции
7.
Для функции
8. Расположите функции, определенные на всей числовой прямой, знаки производных которых указаны на рисунках, по возрастанию количества точек минимума
3.
9.
Абсциссой точки перегиба графика
функции
6. Дифференциал функции
Для
приближенного вычисления значения
функции y(x)
в точке
пример:
1.
2.
3.
4.
5.
6.
7.
|
.
|

ТАБЛИЦА ИНТЕГРАЛОВ
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]() 12.
12.![]()
13.![]() 14.
14.![]()
15.![]() 16.
16.![]()
Неопределённый интеграл
1.
Неопределенный интеграл
![]() равен …(используй
формулу 3)
равен …(используй
формулу 3)
|
|
|
|
|
||||
|
2.Неопределенный
интеграл
|
|
|
(используй формулу 2) |
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
3.
Неопределенный интеграл
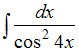 равен …(используй
формулу 12 и раздели на к, то есть на 4)
равен …(используй
формулу 12 и раздели на к, то есть на 4)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() …(используй
формулу 10)
…(используй
формулу 10)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
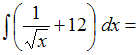 …
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Напоминаем,
что интеграл суммы двух функций равен
сумме интегралов этих функций
![]() и
постоянный множитель можно выносить
за знак неопределенного интеграла:
и
постоянный множитель можно выносить
за знак неопределенного интеграла:
![]() Тогда,
используя формулу
Тогда,
используя формулу
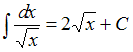 ,
получим:
,
получим:

Неопределенный
интеграл
 равен …
равен …
|
|
|
|
|
Решение:
Напоминаем,
что постоянный множитель можно выносить
за знак неопределенного интеграла:
![]() Тогда,
используя формулу
Тогда,
используя формулу
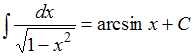 ,
получим:
,
получим:
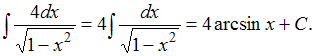
Интегрирование подстановкой
1.Неопределенный
интеграл
![]() равен …
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Обращаем
внимание, что подстановка
![]() приводит
рассматриваемый интеграл к табличному:
приводит
рассматриваемый интеграл к табличному:
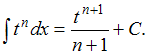 Найдем
дифференциал от обеих частей подстановки:
Найдем
дифференциал от обеих частей подстановки:
![]() ,
тогда
,
тогда
![]() Подставим
получившиеся выражения в исходный
интеграл:
Подставим
получившиеся выражения в исходный
интеграл:
 Заменив
Заменив
![]() его
выражением из подстановки, получим:
его
выражением из подстановки, получим:

2.
Неопределенный интеграл
![]() равен …
равен …
|
|
|
|
|
![]() Заменив
Заменив
![]() его
выражением из подстановки, имеем
его
выражением из подстановки, имеем
![]()
3. …
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Подстановка
![]() приводит
рассматриваемый интеграл к табличному:
приводит
рассматриваемый интеграл к табличному:
![]() Найдем
дифференциал от обеих частей подстановки:
Найдем
дифференциал от обеих частей подстановки:
![]() ,
тогда
,
тогда
![]() Подставим
получившиеся выражения в исходный
интеграл:
Подставим
получившиеся выражения в исходный
интеграл:
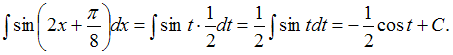 Заменив
Заменив
![]() его
выражением из подстановки, получим:
его
выражением из подстановки, получим:




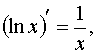
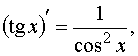
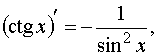
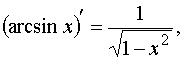



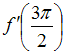 принимает
значение, равное … 5
принимает
значение, равное … 5






 По
формуле
По
формуле