2. Выпуклость и вогнутость
Дифференцируемая
функция
называется выпуклой (вогнутой) или
выпуклой вверх (вниз) на интервале
(a; b),
если она удовлетворяет следующему
условию: для любых различных точек x1,
x2(a;b)
часть графика функции y = f(x),
соответствующая интервалу (x1; x2),
расположена выше (ниже) отрезка M1M2,
где M1(x1;
f(x1)),
M2(x2;
f(x2)).
Т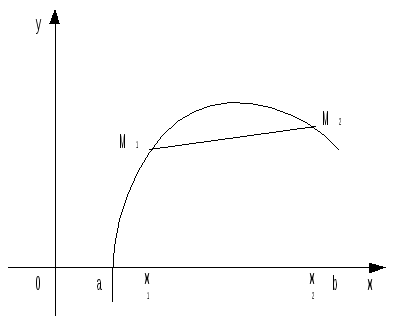
очка
графика функции, разделяющая выпуклый
и вогнутый участки графика, называется
точкой перегиба (часто точкой перегиба
называют абсциссу этой точки графика
функции).
Теорема 5. Если для функции f(x), дважды дифференцируемой в
(
a;
b),
(
)
при всех
x(a; b), то функция f(x) является выпуклой (вогнутой) на (a; b) .
Теорема 6.
Пусть функция f(x)
дважды дифференцируема на (a; b).
Точка x0(a; b)
является точкой перегиба в том и только
в том случае, если одновременно выполняются
два условия: 1)
;
2) при переходе через точку x0
меняет свой знак.
В
последней теореме при условии трижды
дифференцируемости функции условие
2) можно заменить на
.
3. Асимптоты
Прямая (L) называется асимптотой графика функции (или просто асимптотой функции), если расстояние d(M; (L)) от точки М на графике функции y = f(x) до прямой (L) стремится к 0 при неограниченном удалении точки М от начала координат.
Различают два вида асимптот: вертикальные и наклонные.
Прямая x = x0 является вертикальной асимптотой, если по крайней мере один из односторонних пределов f(x0 – 0), f(x0 + 0) равен – или +.
Наклонная асимптота y = kx + b соответствует случаю x – или x + . Коэффициенты k и b при x + находятся из равенств
, 
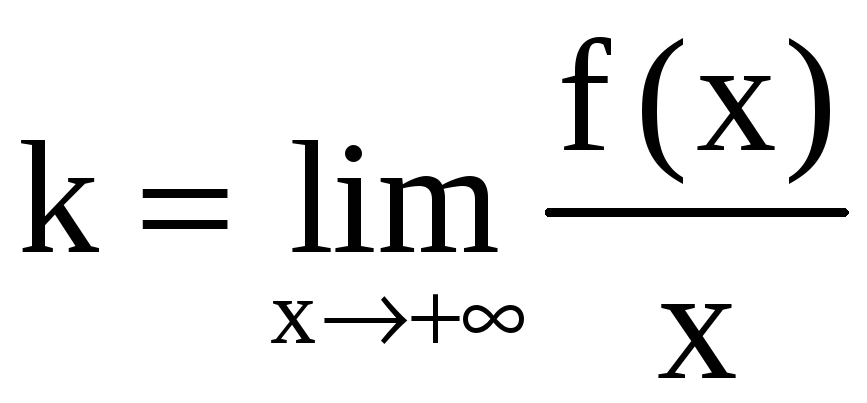(то же при x – ). Если же не существует одного из пределов или один из этих пределов равен – или + , то у функции отсутствует наклонная асимптота при x + (то же при x – ).
4. Построение графика функции
При построении графика функции сначала проводят исследование функции. При этом придерживаются следующего (примерного) плана:
1) находят область определения функции; 2) указывают точки пересечения с осями координат; 3) определяют точки разрыва и устанавливают тип разрыва; 4) с помощью первой производной устанавливают интервалы монотонности (т.е. интервалы возрастания и убывания) функции и находят точки экстремума и значения функции в этих точках; 5) с помощью второй производной устанавливают интервалы выпуклости, вогнутости и находят точки перегиба;
6) находят асимптоты функции. Затем по этим данным строят график функции.
Пример
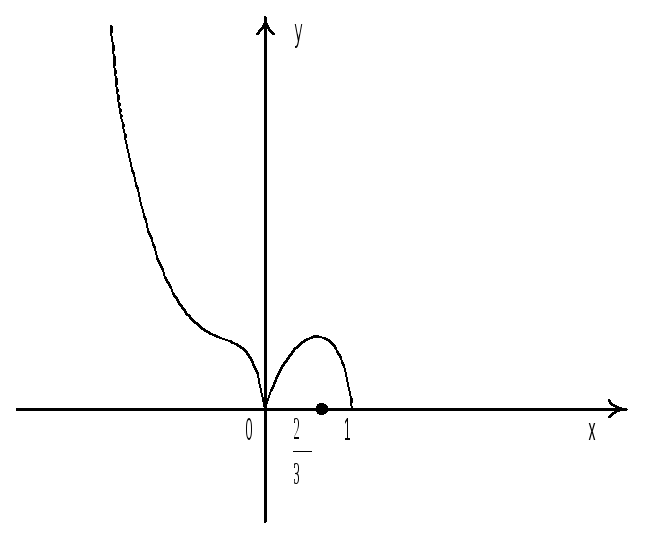
3. Построить
график функции
.
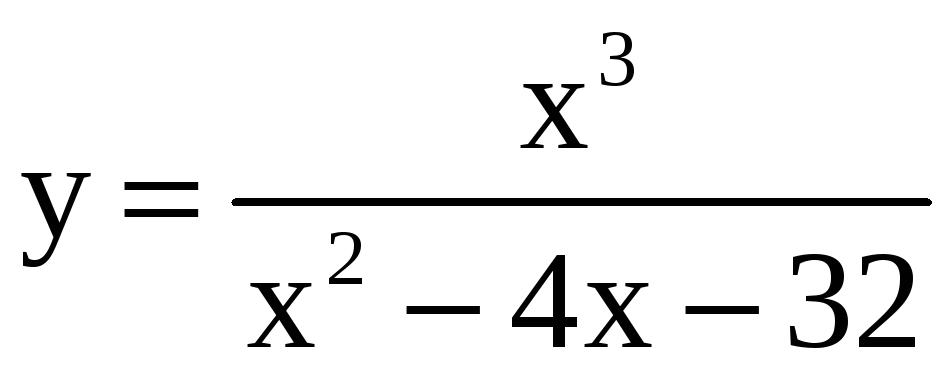Решение.
1) Нулями
знаменателя являются
и
.
Следовательно, областью определения
функции является множество
.
2) Найдём точки пересечения с осями координат:
а)
c
осью 0x
. Найдём нули функции:
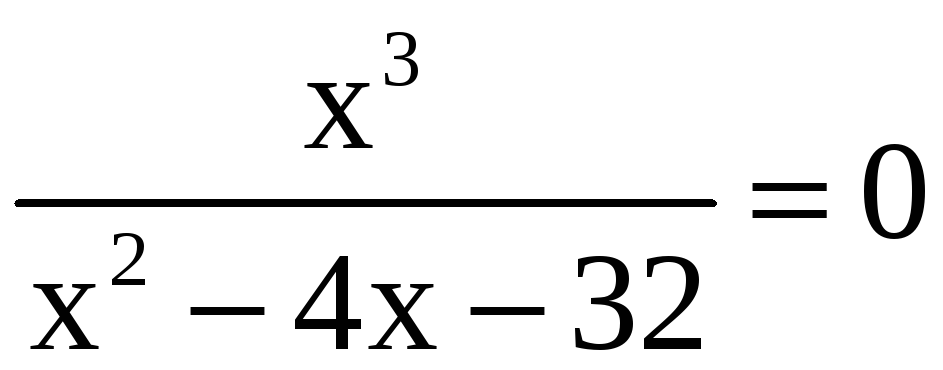лишь при
x = 0; значит, график функции пересекает ось 0x (или касается оси 0x ) в точке O(0; 0) – начале координат;
б) c осью 0y . Для нахождения общей точки графика функции и оси 0y следует найти f(0): f(0) = 0. Поэтому график пересекает ось 0y в точке O(0; 0).
3) Наша
функция представляет собой отношение
двух многочленов, поэтому она непрерывна
всюду, за исключением нулей знаменателя:
и x
= 8. Найдём левые и правые пределы в этих
точках.
Для
точки
:
;
.
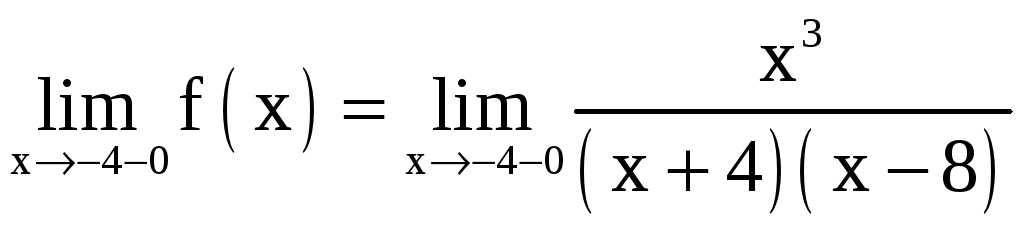
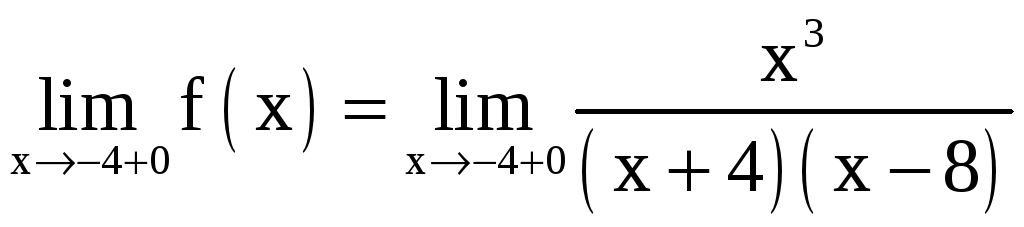
Отсюда
делаем вывод, что
является точкой разрыва второго рода.
Для точки x = 8:
;
.
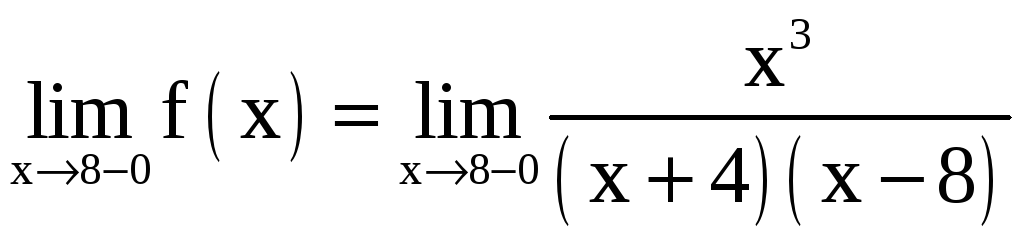
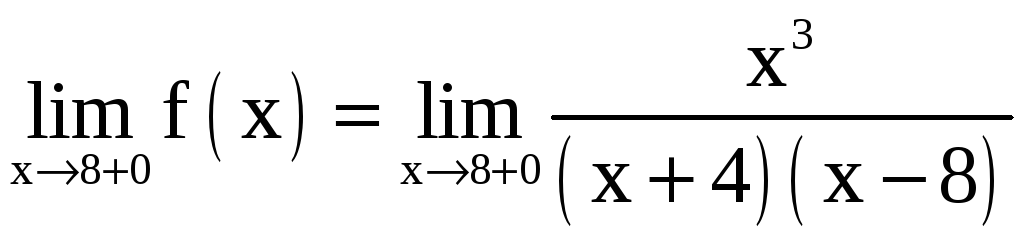
Поэтому x = 8 также является точкой разрыва второго рода.
4) Имеем
.
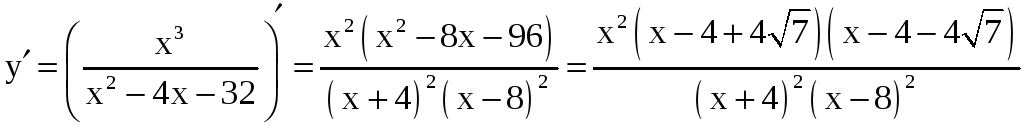Критическими
точками функции являются её стационарные
точки
,
,
.
Знак
совпадает со знаком выражения
.
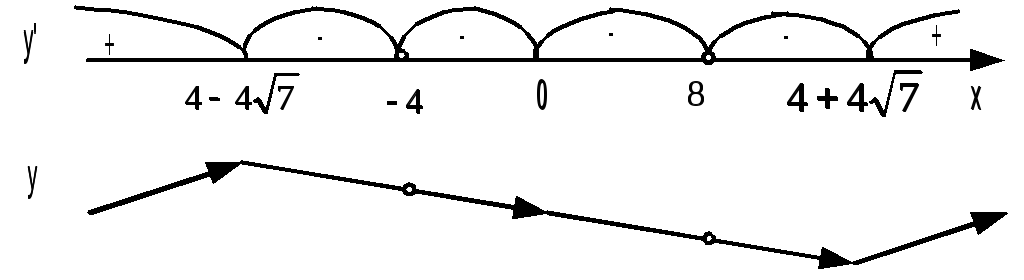
Видно,
что функция возрастает на промежутках
и
и убывает на промежутках
,
,
.
Следовательно, точка
является точкой максимума (на рисунке
ей соответствует «горка»), точка
– точкой минимума (ей соответствует
«впадина»). Стационарная точка
не является точкой
экстремума. Найдём значение функции в
точках экстремума: f(
)
–7,57; f(
)
25,35.
5)
.
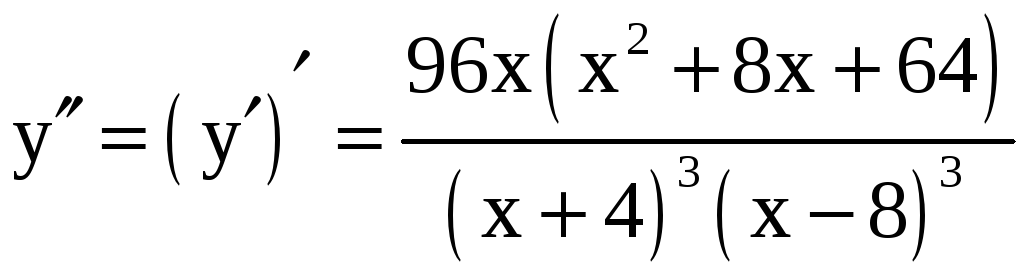Трёхчлен
при всех x
(его дискриминант меньше 0). Поэтому знак
совпадает со знаком дроби
.
Составим схему. Видно, что функция выпукла в интервалах (–; –4)
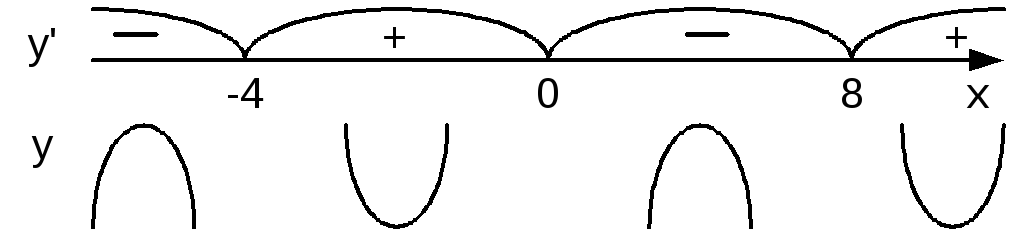
и (0; 8) и
вогнута в интервалах (–4; 0) и (8; +).
При переходе через точки – 4, 8, 0
меняет свой знак. Поэтому точка x
= 0 является точкой перегиба (в точках x
=
4, x
= 8 функция не определена).
6)
Так как
,
,
то прямые
и x
= 8 являются вертикальными асимптотами.
Найдём наклонные асимптоты при x
–
и при x
+.
Уравнения этих асимптот будем искать
в виде y
= kx
+ b:
а) x –.
,
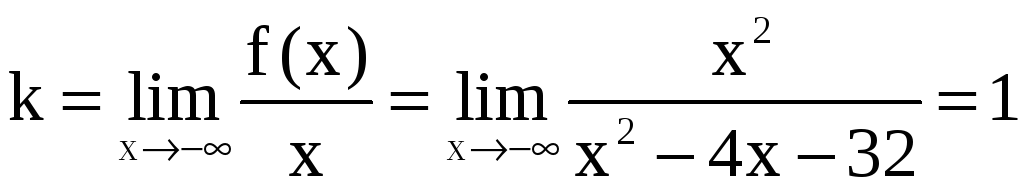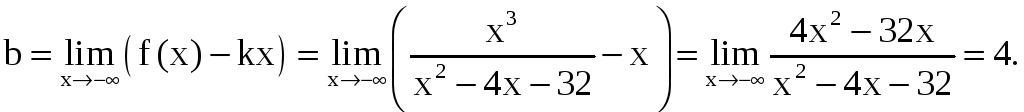
Таким образом, прямая y = x + 4 является асимптотой при x –;
б) при x + получим тот же результат: прямая y = x + 4 является асимптотой.
Основываясь на полученных данных, построим график функции.
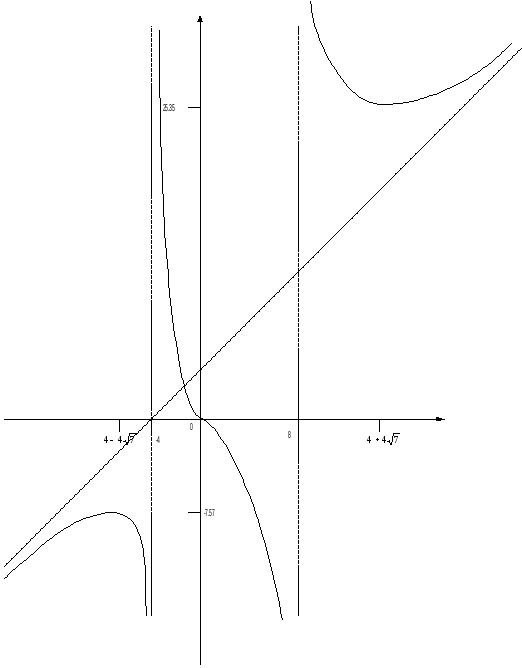
Пример
4. Построить
график функции
.
Решение. 1) Областью определения функции является (–; +).
2) Найдём точки пересечения с осями координат:
а) c осью 0x. Функция не имеет нулей, следовательно, она не имеет общих точек с осью 0x;
б)
c
осью 0y.
Имеем
.
Точка (0; e-4)
является точкой пересечения графика с
осью 0y.
3) Наша функция является суперпозицией непрерывных функций, поэтому она непрерывна на всей числовой оси.
4) Имеем
.
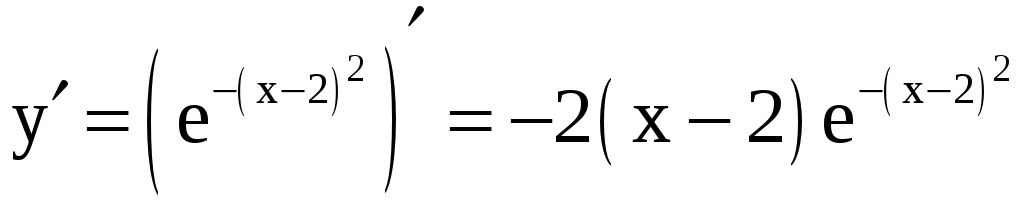Ф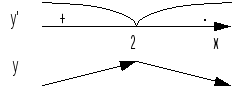
ункция
имеет одну стационарную точку
.
Функция
возрастает на промежутке (–;
2) и убывает на промежутке (2; +),
точка x = 2
является точкой максимума. Максимум
функции равен
.
5)
.
Ф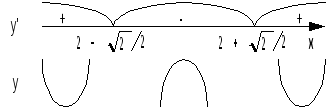
ункция
имеет нули x1=2–
,
x2=2+
.
Она выпукла на интервале
(2–
; 2+
)
и вогнута на интервалах (–; 2–
),
(2+
; +
).
Точки x
= 2 –
и x
= 2 +
являются точками перегиба.
6) Так как функция определена и непрерывна на всей числовой оси, то она не имеет вертикальных асимптот. Найдём наклонные асимптоты.
а) x – . Ищем асимптоту в виде y = kx + b.
,
.
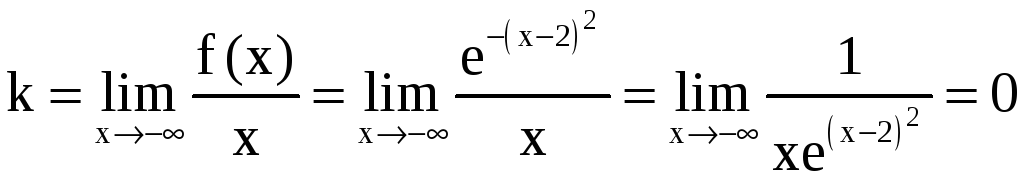Таким
образом, прямая
является асимптотой функции при
x –.
б)
При x
+
получим тот же результат:
является асимптотой при x
+.
По полученным данным построим график функции.
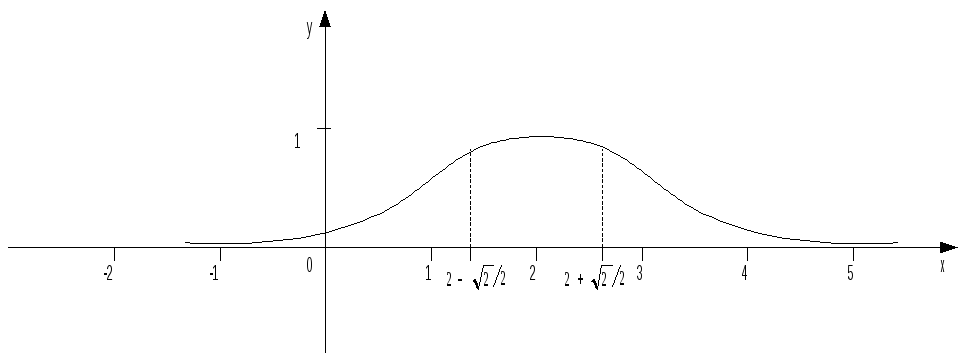
Пример
5. Построить
график функции
Решение. 1) Область
определения функции
,
.
2) Точки пересечения с осями координат
;
; 
;
; 
3) Функция непрерывна на всей области определения.
4)
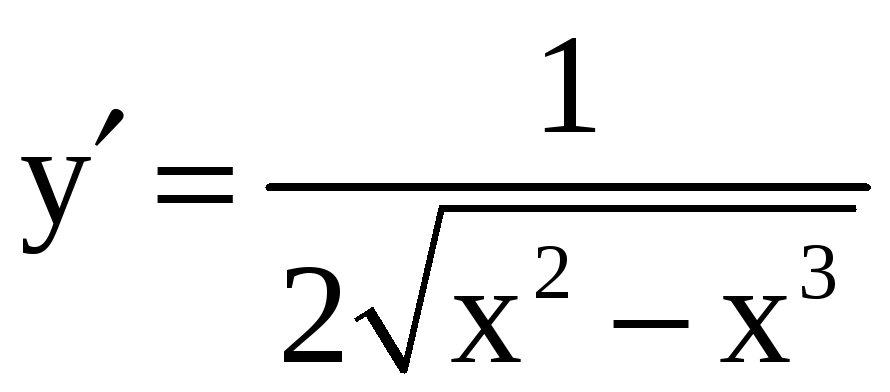
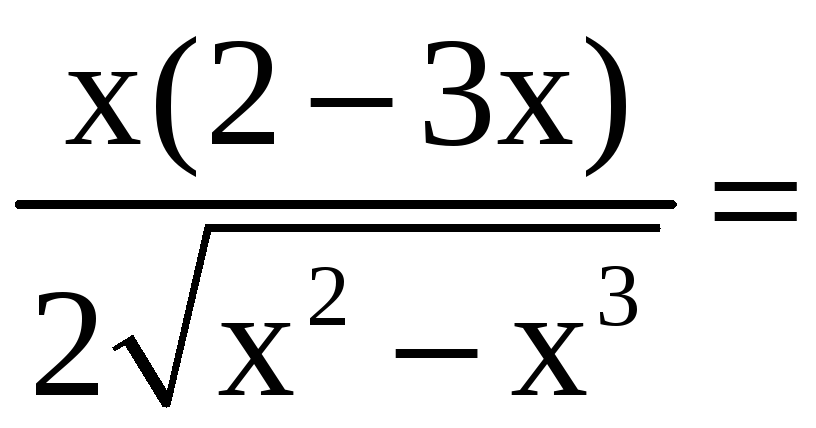
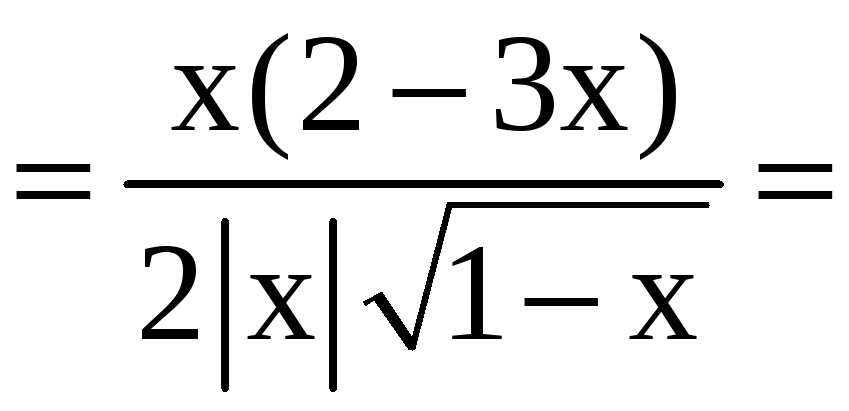
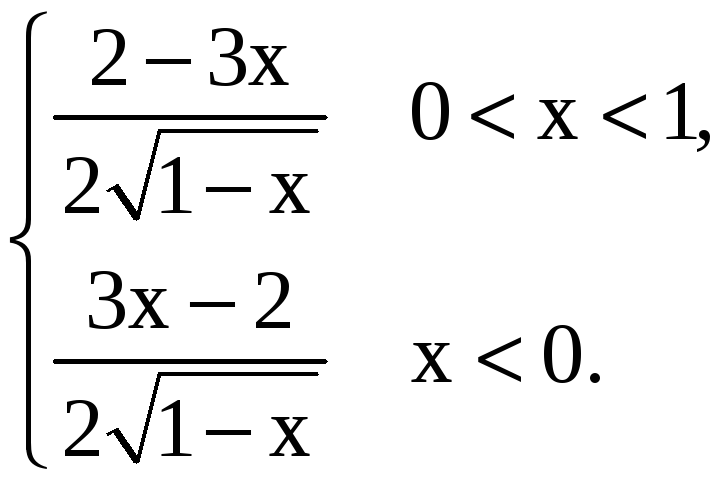
Следовательно,
производная
в
точке
не определена.
, 
, 
стационарная точка.
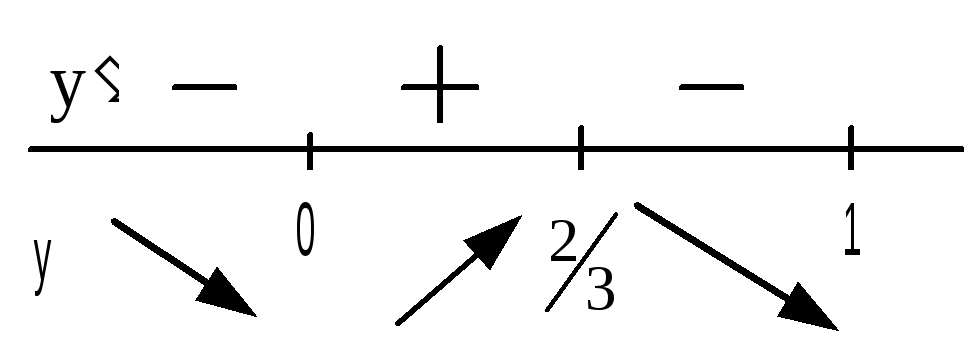
Функция убывает
на промежутках
и возрастает на промежутке
Следовательно,
точка
является точкой максимума;
критическая
точка, является точкой минимума.
,
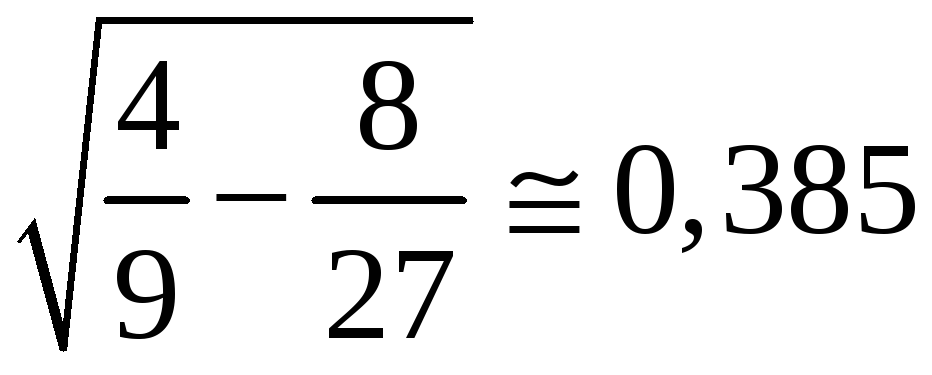График данной функции приведен на рисунке.
