
- •Моделирование систем и сетей массового обслуживания
- •Потоки событий
- •Простейший поток событий
- •Общая характеристика систем массового обслуживания
- •Элементарный акт обслуживания заявки
- •Структуры смо
- •Описание функционирования смо
- •Дисциплины ожидания и обслуживания
- •Обозначения и классификация смо
- •Показатели эффективности и основные характеристики смо
- •Основные характеристики простейших смо
- •Общие принципы моделирования систем массового обслуживания
- •Метод статистических испытаний
- •Генерация входных потоков
- •Модель функционирования элементарных смо
- •Модель смо с ожиданием
- •Модель смо без ожидания
-
Модель смо с ожиданием
Рассмотрим одну из простейших систем обслуживания М/М/1, её модель представлена на рис. 3.8. Из обозначения системы следует: процесс поступления заявок ‑ пуассоновский, объем буферной памяти не ограничен, распределение времени обслуживания ‑ экспоненциальное. Заявки обслуживаются по принципу FIFO.

Рис. 3.8. Модель системы обслуживания М/М/1
Предположение о бесконечности числа мест для ожидания в системе представляется вполне обоснованным, так как проблемы с недостатком памяти возникают все реже и в ближайшем будущем, по-видимому, перестанут вызывать практические затруднения.
Основные характеристики системы обслуживания М/М/1
-
Коэффициент загрузки устройства – ρ
ρ= λ m1{tобсл}= λ /μ <1,
где λ – интенсивность потока заявок,
m1{tобсл} – среднее значение времени обслуживания, m1{tобсл}=1/μ,
μ – интенсивность обслуживания.
Пусть СМО работает достаточно длительное время T, тогда число заявок в системе равно λT, среднее время обслуживания заявок – λ T m1{tобсл}, а вероятность обслуживания заявки:
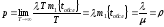 .
.
Таким образом, коэффициент загрузки является вероятностью обслуживания заявки в канале.
Коэффициент загрузки имеет смысл только для установившихся режимов.
-
Коэффициент простоя канала (вероятность того, что в устройстве нет заявки)– η
η=1-ρ.
-
Время ожидания заявки в системе –tож;
-
Время пребывания заявки в системе ‑ tc
tc=tож +m1{tобсл},
-
Средняя длина очереди ‑ l
l=λ m1{tож}
-
Среднее число заявок в системе – m1{n}
m1{n}=λ (tож +m1{tобсл}).
-
Модель смо без ожидания
Рассмотрим простую СМО, которая состоит из трёх одинаковых каналов; входной поток ‑ простейший с параметром ; время обслуживания в канале одной заявки постоянно и равно tобсл. Данная СМО является системой без ожидания, т.е. заявка, заставшая все каналы занятыми, покидает систему. Дисциплина обслуживания такова: если в момент поступления k-ой заявки первый канал свободен, то он приступает к обслуживанию заявки; если этот канал занят, то заявку обслуживает второй канал и т.д. Надо определить, сколько заявок в среднем обслужит система за время Т и сколько в среднем она даст отказов.
За начальный момент расчета выбирают момент поступления первой заявки t1 = 0. Введем следующие обозначения: tк - момент поступления k-ой заявки; tk ‑ промежуток времени между поступлением в систему k-ой и (k + 1)-ой заявки; ti — момент окончания обслуживания требования i-ым каналом.
Предположим,
что в момент t1
все
каналы свободны. Первая заявка поступает
в первый канал, в течение времени
обслуживания  этот канал занят. Поэтому полагают
T1=t1+
этот канал занят. Поэтому полагают
T1=t1+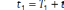
 ,
добавляют единицу к счетчику обслуженных
заявок и переходят к рассмотрению второй
заявки.
,
добавляют единицу к счетчику обслуженных
заявок и переходят к рассмотрению второй
заявки.
Предположим,
что k
заявок
уже
рассмотрено. Определим момент поступления
(k+1)-ой
заявки. Для этого найдем очередное
значение xk
равномерно
распределенной случайной величины,
вычислим очередное значение экспоненциально
распределенной случайной величины
tk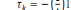 ,
а
затем момент поступления (k+1)-ой
заявки tk+1=
tk+tk
,
а
затем момент поступления (k+1)-ой
заявки tk+1=
tk+tk .
.
Чтобы
узнать, свободен ли в этот момент первый
канал, необходимо проверить условие
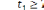
 .
Если
это условие выполнено, то к моменту tk+1
первый канал освободился и может
обслуживать заявку. В этом случае T1
присваивается
значение
tk+1+
.
Если
это условие выполнено, то к моменту tk+1
первый канал освободился и может
обслуживать заявку. В этом случае T1
присваивается
значение
tk+1+
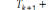 ,
добавляется
единица к счетчику обслуженных заявок
и происходит переход к следующей заявке.
,
добавляется
единица к счетчику обслуженных заявок
и происходит переход к следующей заявке.
Если

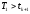 ,
то
первый канал в момент tk+1
занят. В этом случае проверяем, свободен
ли второй канал. Если условие
,
то
первый канал в момент tk+1
занят. В этом случае проверяем, свободен
ли второй канал. Если условие 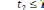
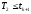 выполнено, присваиваем t2
значение
tk+1+
выполнено, присваиваем t2
значение
tk+1+
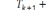 ,
добавляем единицу к счетчику обслуженных
заявок и переходим к следующей заявке.
,
добавляем единицу к счетчику обслуженных
заявок и переходим к следующей заявке.
Если
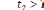
 ,
то
проверяем условие
,
то
проверяем условие
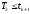 .
.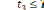 Если
все каналы оказались заняты, то в этом
случае прибавляем единицу в счетчик
отказов и переходим к рассмотрению
следующей заявки. Результаты моделирования
можно оформить в виде таблицы регистрации
результатов имитации одной реализации
(табл. 3.1).
Если
все каналы оказались заняты, то в этом
случае прибавляем единицу в счетчик
отказов и переходим к рассмотрению
следующей заявки. Результаты моделирования
можно оформить в виде таблицы регистрации
результатов имитации одной реализации
(табл. 3.1).
Таблица 3.1
|
№ заявки (k) |
Случайное число xk |
tk |
Момент поступления заявки tk |
Момент окончания обслуживания заявки i-ым каналом |
Счетчик обслуженных заявок |
Счетчик отказов |
||||
|
i=1 |
i=2 |
i=3 |
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Каждый раз, вычислив tk+1, надо проверить еще условие окончания реализации tk+1>T. Если это условие выполнено, то одна реализация случайного процесса функционирования системы воспроизведена и опыт заканчивается. В счетчике обслуженных требований и в счетчике отказов находятся числа nо6сл и потк.
Получив п реализаций случайного процесса, т.е., повторив такой опыт п раз, определяют оценки математических ожиданий числа обслуженных требований m1{по6с} и числа требований, получивших отказ m1{потк}.

