2. Простейший поток событий

ПС называется простейшим, если он обладает свойствами ординарности, стационарности и отсутствием последействия. Понятие простейшего потока событий играет большую роль, т.к. на практике достаточно часто встречаются близкие к нему потоки. Кроме того, при суммировании достаточно большого числа ординарных потоков с практически любым последействием образуется поток близкий к простейшему.

Число событий n, наступивших в ПС за время T, является случайной дискретной величиной. Установлено, что в простейшем ПС число событий n на временном интервале T подчиняется закону Пуассона, поэтому простейший ПС часто называют потоком Пуассона.

Дифференциальная функция распределения вероятности наступления n событий за время T

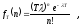(2.40)

где λ – параметр распределения Пуассона,

n =0, 1, 2,….

Среднее число событий в потоке Пуассона за время T

. (2.41)

Из последнего выражения следует, что параметр λ закона Пуассона определяет интенсивность простейшего потока событий.

Установлено, что если поток событий подчиняется закону Пуассона с параметром , то закон распределения вероятностей значений случайных интервалов ∆t между двумя последовательными событиями является экспоненциальным с тем же параметром .

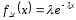(3.1)

Математическое ожидание и дисперсия интервалов ∆t, распределённых по экспоненциальному закону, определяются:

.

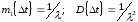Таким образом, величина среднего интервала времени между двумя последовательными событиями простейшего потока ∆t_ср обратно пропорциональна интенсивности потока . Этой же величине равно и среднеквадратичное отклонение случайного интервала ∆t от ∆t_ср, определяемое как корень из дисперсии:

.

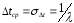Важное свойство экспоненциального закона распределения состоит в том, что вероятность наступления очередного события через интервал времени ∆t не зависит от момента появления предшествующего события. Это свойство является следствием независимости поступления событий во времени (отсутствием последствия).

3. Общая характеристика систем массового обслуживания

Под системой массового обслуживания (СМО) понимают динамическую систему с ограниченными ресурсами, предназначенную для эффективного обслуживания случайного потока заявок. СМО называют также Q-системами (англ. queuing system).

К СМО относятся ЭВМ, вычислительные центры, телефонные станции, билетные кассы, аэродромы, РЛС, любые информационные системы. Проблемы родственные задачам массового обслуживания, постоянно возникают и в других областях (при эволюции в биологии, организации различного рода перевозок, организации работы культурно-бытовых предприятий, при ремонте и обслуживания оборудования и т.п.). Обобщенная схема СМО приведена на рис. 3.2.

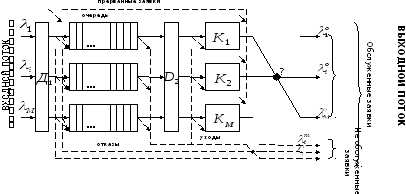
потери

Рис. 3.2 Обобщенная схема СМО

‑ обязательные связи; --- возможные связи

В СМО поступают через случайные промежутки времени заявки разных типов, число типов заявок конечно и равно М. Тип заявки определяется порождающей её причиной. Совокупность заявок все типов образует входной поток СМО.

Входной поток заявок рассматривается как поток событий, его распределение в основном определяет характер процесса массового обслуживания. Интенсивность потока заявок i-ого типа обозначаются .

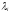СМО содержит конечное число элементов обслуживания, называемых каналами обслуживания (К). Обслуживание заявок выполняются М каналами (К). Каналы обслуживания делятся на универсальные и специализированные. Канал считается универсальным, если известны его функции распределения продолжительности обслуживания для заявок каждого типа (t_обсл ‑ продолжительность обслуживания заявки). Если функции распределения продолжительности обслуживания заявок известны не для всех типов заявок, то канал считается специализированным.

Если в момент поступления заявки есть свободный канал обслуживания, обслуживание заявки начинается немедленно. Если все каналы заняты, заявка занимает место в очереди. Если число мест в очереди ограничено, и все они заняты, то возникший конфликт может быть решен двумя способами:

• система отказывается принять заявку;

• система принимает заявку за счет выталкивания из очереди другой, менее ценной в данный момент заявки.

В общем случае промежутки времени ∆t, через которые в систему поступают заявки, и продолжительность обслуживания t_обсл одной заявки конечны и случайны, поэтому процесс обслуживания случаен и в нем возможны как перегрузки, так и простои.

Управление процессом продвижения заявок и их обслуживанием в СМО осуществляется с помощью специальных правил, называемых дисциплинами ожидания и обслуживания. Дисциплина ожидания D₁ определяет порядок приема заявок в систему и размещения их в очереди, а дисциплина обслуживания D₂ ‑ порядок выбора очереди, если их несколько, и порядок выбора заявок из очереди для обслуживания.

Обслуженные и по разным причинам не обслуженные заявки покидают систему, образуя выходной поток.