12. Характеристические функции
1. Дать определение характеристической функции.
Характеристической функцией случайной величины называется функция от вещественной переменной:
=
-формула
преобразования Фурье-Стилтьеса
2. Записать формулы для вычисления характеристической функции дискретных случайных величин.
3. Записать формулы для вычисления характеристической функции непрерывных случайных величин.
4. Как по заданной характеристический функции найти плотность вероятностей случайной величины?
5. Чему равно значение характеристической функции в нуле?
ХФ в нуле равняется единице.
6. Чему равна характеристическая функция случайных величин связанных линейной зависимостью?
η=aξ+b
a,b=const 
7. Чему равна характеристическая функция суммы независимых случайных величин?
𝛏=
+
-независимые
СВ
8. Чему равна характеристическая функция вырожденной случайной величины?
9. Чему равна характеристическая функция распределения Пуассона?
10. Чему равна характеристическая функция равномерно распределенной случайной величины?
11. Чему равна характеристическая функция гауссовского распределения?
12. Как вычислить начальные моменты с использованием характеристической функции?
13. Как определяются кумулянты случайной величины?
Кумулянты(семиинварианты)
случайной величины – коэф. разложения
логарифма ХФ СВ в степенной ряд
.Тогда
кумулянтом порядка k наз. Действительное
число которое равняется:
,
k=1,2,3…n
14. Как
первые четыре кумулянта связанны с
начальными и центральными моментами
случайной величины?
15. Чему равны кумулянты суммы двух независимых случайных величин?
-независимые
СВ
-
Предельные теоремы
1.Чему равен коэффициент вариации?
2. Перечислить основные виды сходимости случайных величин.
(1)С вероятностью 1,(2) по вероятности,(3) в среднеквадратическом,(4) по распределению.
3. Что такое сходимость с вероятностью единица?
Последовательность
случайных величин 
сходится к случайной величине ξ
почти
наверное,
или с вероятностью 1, если
4. Что такое сходимость по вероятности?
Последовательность
случайных величин 
сходится к случайной величине ξ
по вероятности,
если для любого ε>0
5. Что такое среднеквадратическая сходимость?
Последовательность
случайных величин 
сходится к случайной величине ξ
в среднеквадратическом,
если
6.Что такое сходимость по распределениям?
7. Как связаны различные виды сходимости?
1
4
2
3
8. В чем заключается центральная предельная проблема?
Центральная предельная проблема теории вероятности представляет собой проблему сходимости законов распредиления последовательности сумм независимых СВ. Нашла решение в виде совокупности теорем наиболее известные среди которых есть закон больших чисел и центральная предельная теорема.
9. Сформулировать центральную предельную теорему Ляпунова.
Если
случайные величины 
распределены одинаково и имеют M{
}=m
D{
}=
M{ξ}=nm
D{ξ}=n
10. Сформулировать интегральную теорему Муавра-Лапласа.
Если
-
случайная величина, имеющая биномиальное
распределение, то
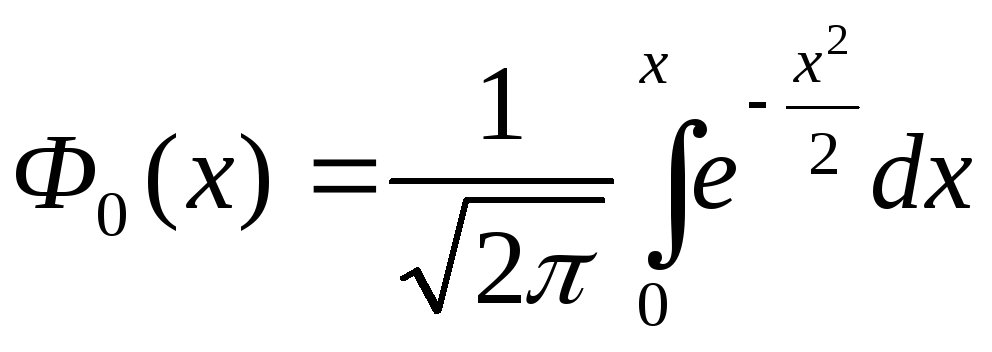
11. Сформулировать локальную теорему Муавра-Лапласа.
Пусть Р(А) — вероятность события А. Тогда вероятность того, что в условиях схемы Бернулли событие А при n испытаниях появится точно m раз, выражается приближенной формулой Лапласа:
12. Сформулировать теорему Пуассона.
Если
в схеме Бернулли
Часто распределение Пуассона наз. Закон распределения редких событий.
13. Дать определение безгранично делимой случайной величины.
СВ
ξ наз. безгранично делимой если её можно
представить в виде
,
-одинаково
распредиленные , независимые СВ, зкон
распредиления которых зависит от n.
14.Привести примеры безгранично делимых случайных величин.
Распредиления:вырожденое,Пуассона,нормальное,Коши,гамма,отрицательное-биномиальное.