8. Функциональные преобразования случайных величин

1. Сформулировать задачу преобразования случайных величин.

Пускай есть СВ ξ которая имеет ФР(x) пусть также задана детерминированая функция y=G(x) получим новую СВ η=G(ξ).Задача (y)-?

2.Привести общий подход к решению задачи преобразования случайной величины

F_η(y)=P{ η<y}=P{ξ<x₁}+P{x₂<ξ<x₃}=F_ξ(x₁)+F_ξ(x₃)-F_ξ(x₂+0)

=(y)

3.Какие проблемы существуют при решении задачи преобразования случайных величин?

Для большенства функций точки выразить не удаётся.Поскольку то меняется расположение точек и их количество.Решение зависит от вида ФР (x).

4.Какие условия накладываются на функцию преобразования для получения решения задачи преобразования случайных величин в явном виде?

Таким образом задача решается в общем виде, если в явном виде найти обратную ф-цию.

5.Привести формулу для функции распределения случайной величины, полученной непрерывным монотонным преобразованием.

F_η(y)=

6.Привести формулу для функции распределения случайной величины, полученной линейным преобразованием.

F_η(y)=

7.Привести формулу для плотности вероятностей случайной величины, полученной непрерывным монотонным преобразованием.

8.Привести формулу для плотности вероятностей случайной величины, полученной линейным преобразованием.

9.Чему равна плотность вероятностей суммы непрерывных случайных величин?

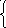
10.Чему равна плотность вероятностей разности двух непрерывных случайных величин?

11.Чему равна плотность вероятностей произведения двух непрерывных случайных величин?

12.Чему равна плотность вероятностей частного двух непрерывных случайных величин?

9. Числовые характеристики случайной величины

1. Дать определение математического ожидания случайной величины.

Мат. ожидание СВ.  с функцией распределения F(x) называется действительное число m, определяемое следующей формулой

если указанный интеграл абсолютно сходится.

2. Привести формулу для вычисления математического ожидания дискретных случайных величин.

3. Привести формулу для вычисления математического ожидания непрерывных случайных величин.

4. Привести формулу для вычисления математического ожидания смешанных случайных величин.

5. Перечислить основные свойства математического ожидания.

1)

2)

3)

4), - независимые СВ

5)

6)

6. Чему равно математическое ожидание постоянной величины? Доказать.

, С – вырожденная СВ. принимающая одно значение с вер. «1». Найдите ее МО

7. Чему равно математическое ожидание произведения постоянной и случайной величины? Доказать.

, Доказательство. Достаточно расписать МО и затем вынести «с» за знак суммы.

8. Чему равно математическое ожидание суммы случайных величин? Доказать.

Доказательство:

9. Чему равно математическое ожидание произведения независимых случайных величин? Доказать.

Доказательство:

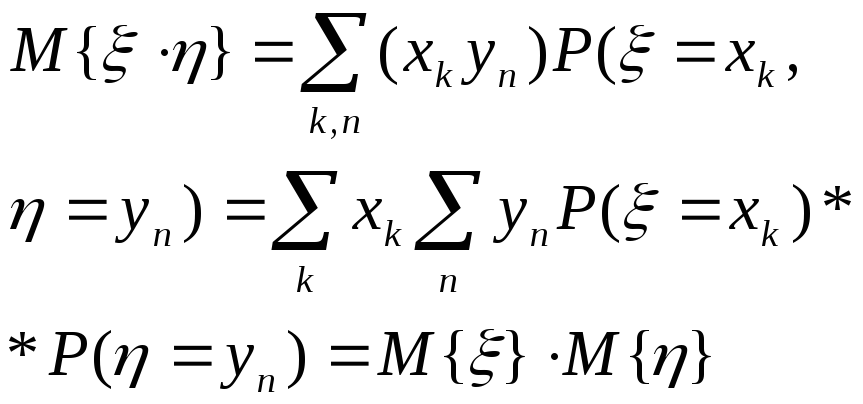
10. Какой смысл имеет математическое ожидание случайной величины?

МО – среднее значение СВ, которое не всегда совпадает со значением дискретной СВ.

11. Какие единицы измерения имеет математическое ожидание? Обосновать ответ.

, так как , а F(x) – безразмерная величина

12. Как определяется дисперсия случайной величины?

13. Привести формулу для вычисления дисперсии дискретных случайных величин.

14. Привести формулу для вычисления дисперсии непрерывных случайных величин.

15. Привести формулу для вычисления дисперсии смешанных случайных величин.

16. Какой смысл имеет дисперсия случайной величины?

Характеристика разброса значений случайных величин относительно МО

17. Перечислить основные свойства дисперсии.

1)

2)

3)

4)Если ξ и η независимы, то

5)

18. Чему равна дисперсия постоянной величины? Доказать.

19. Чему равна дисперсия случайной величины, умноженной на постоянную величину? Доказать.

20. Чему равна дисперсия суммы независимых случайных величин? Доказать.

21. Какие единицы измерения дисперсии?

22. Дать определение среднего квадратического отклонения. Какие единицы измерения среднего квадратического отклонения?

23. Чему равно среднее квадратическое отклонение суммы двух независимых случайных величин?

24. Записать неравенства Чебышева.

25. Как определяется центрированная случайная величина?

26. Чему равно математическое ожидание центрированной случайной величины? Доказать.

27. Чему равна дисперсия центрированной случайной величины? Доказать.

28. Как определяется нормированная случайная величина?

29. Чему равно математическое ожидание нормированной случайной величины? Доказать.

30. Чему равна дисперсия нормированной случайной величины? Доказать.

31. Как определяется стандартная случайная величина?

32. Чему равно математическое ожидание стандартной случайной величины? Доказать.

33. Чему равна дисперсия стандартной случайной величины? Доказать.

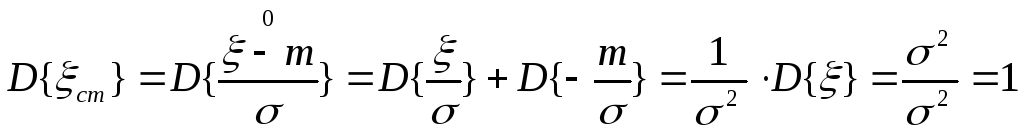
34. Дать определение начальных моментов случайной величины.

35. Дать определение центральных моментов случайной величины.

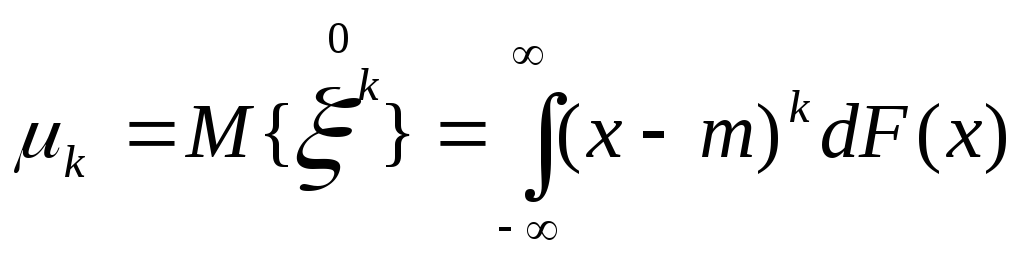
36. Какие единицы измерения начальных моментов случайной величины?

37. Какие единицы измерения центральных моментов случайной величины?

38. Записать формулу для вычисления начальных моментов дискретных случайных величин.

39. Записать формулу для вычисления начальных моментов непрерывных случайных величин.

40. Записать формулу для вычисления центральных моментов дискретных случайных величин.

41. Записать формулу для вычисления центральных моментов непрерывных случайных величин.

42. Записать формулу, выражающую дисперсию через начальные моменты случайной величины.

43. Дать определение коэффициента асимметрии.

44. Какой смысл коэффициента асимметрии?

Показывает насколько не симетричным является распределение

45. Дать определение коэффициента эксцесса.

46. Какой смысл коэффициента эксцесса?

Показывает степень островершинности распределения по отношению к нормальному