6. Случайная величина

1. Дать определение случайной величины.

Случайной величиной, замкнутой на вероятностном пространстве называется функция с областью определений и областью значений . При этом для всех должно выполнятся условие:

2. Дать определение закона распределения случайной величины.

ЗР - Любое правило, которое связывает возможные значения случайной величины и их вероятности.

3. Дать определение функции распределения случайной величины.

ФР(F(x) – вероятность того,что значение случайной величины будет меньше некоторого определенного значения

4. Перечислить основные свойства функции распределения случайной величины.

1)ФР – неубываемая

2)ФР неприрывная слева

3) ,

4)

5)

6)[F(x)]=1 – безразмерная величина

5. Как с помощью функции распределения вычислить вероятность попадания случайной величины в заданный интервал?

6. Чему равна вероятность того, что случайная величина примет конкретное значение? Обосновать ответ.

7. Какие единицы измерения имеет функция распределения? Обосновать ответ.

[F(x)]=1 – безразмерная величина

8. Какие виды случайных величин существуют?

Дискретные, непрерывные, смешанные

9. П ривести примерные графики функции распределения для различных видов случайных величин.

Дискретные

10. Что такое ряд распределения?

11. Что называется плотностью вероятностей?

12. Перечислить основные свойства плотности вероятностей.

1)

2) - неотрицательность

3) - свойство нормировки

4)

5)

13. Какие единицы измерения имеет плотность вероятностей? Обосновать ответ.

, так как , а F(x) – безразменрная величина

14. Имеются ли ограничения на максимальное значение плотности вероятностей? Обосновать ответ.

Нету р(х)>0

15. Как с помощью плотности вероятностей найти вероятность попадания случайной величины в заданный интервал?

16. Как с помощью плотности вероятностей найти функцию распределения?

7. Случайный вектор

1. Дать определение многомерной случайной величины.

Рассмотрим вероятностное пространство , на котором определены n случайных величин вектор - Называется n-мерной случайной величиной.

2.Дать определение функции распределения случайного вектора.

ФР случайного вектора – вероятность совместного(одновременного) выполнения следующих событий .ФР может быть записана в виде:F()=P(,где

3.Перечислить основные свойства многомерной функции распределения.

1) есть неубывающая функция по каждому аргументу.

2) непрерывна слева по каждому аргументу.

3)

4)

5)

4.Дать определение частного распределения.

Это любое распредиление любого подмножества СВ взятых из случайного вектора.

5.Как найти частное распределение с помощью многомерной функции распределения?

6.Перечислить основные виды случайных векторов.

Дискретные, непрерывные.

7.Что такое матрица распределений? Какие у нее свойства?

Матрицой распределения называется матрица вида:

, где m – число случайных величин в векторе, а e – число принимаемых значений.

Свойства:

8.Как получить частные распределения для двумерного дискретного случайного вектора?

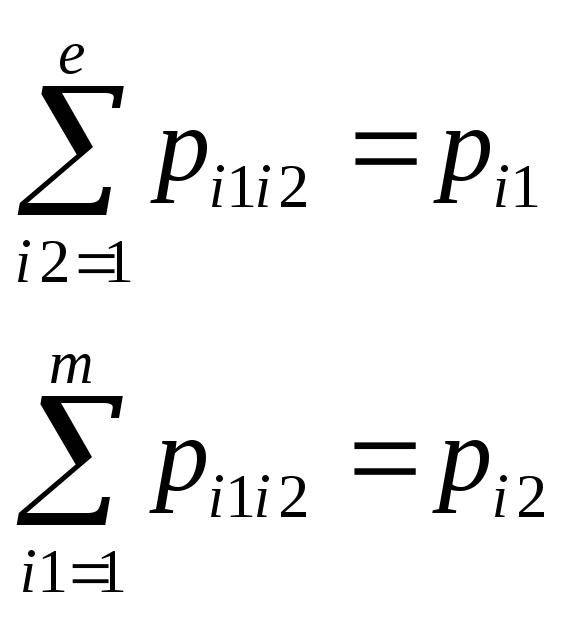Это свойство позволят найти частное распредиление СВ входящих в вектор.

9.Как определяется плотность вероятностей многомерных непрерывных случайных величин?

10.Перечислить основные свойства плотности вероятностей случайного вектора.

11.Как получить частные распределения для непрерывных случайных величин?

12.Дать определение условного закона распределения.

Условным законом распредиления СВ наз. Распредиление СВ при условии того что СВ приняла конкретное значение или находится на некотором промежутке.

13.Как определяется условное распределение для дискретных случайных величин?

14.Как определяется условное распределение для непрерывных случайных величин?

15.Дать общее определение независимых случайных величин.

Если условная ФР равняется безусловной,то такие величины наз. независимыми.

16.Сформулировать условие независимости дискретных случайных величин.

17.Сформулировать условие независимости непрерывных случайных величин.