§ 8.1. Необходимые и достаточные признаки симметрии

Рассмотрим математическую формулировку преобразований симметрии.

Введем некоторый оператор , который действует на любое состояние системы по правилу:

,

где - новое состояние системы.

И потребуем, чтобы обратное преобразование переводило систему обратно в исходное состояние, т.е.

.

Таким образом, из этих соотношений следует, что , т.е. произведение и есть тождественное преобразование.

Все операции в квантовой механике инвариантны относительно этого преобразования. Рассмотрим оператор : и подействуем на это выражение оператором :

.

Если на систему еще подействовать тождественным оператором , то мы получаем такое выражение:

.

Обозначим оператор и тогда получим выражение:

.

Таким образом, любое соотношение между физическими величинами после преобразования не меняет вид:

.

Найдем класс преобразований, которые оставляют без изменения измерения. Для этого выясним вид оператора, при котором амплитуда вероятности оставалась бы без изменений. Потребуем, чтобы . Подробнее рассмотрим :

.

Таким образом, из рассмотренного соотношения вытекает, что данное преобразование оставляет амплитуду вероятности неизменной, если равен единичному оператору, т.е.

.

А это есть унитарное преобразование.

При унитарном преобразовании эрмитовский оператор переходит в эрмитовский. Покажем это. Пусть - эрмитовский оператор. Докажем, что после унитарного преобразования тоже будет эрмитовским оператором. Здесь . То есть нужно доказать тот факт, что если , то после преобразования должно получиться .

.

Унитарное преобразование есть преобразование симметрии данной физической системы, если после преобразования не меняются уравнения физической системы.

Будем исходить из уравнения Шредингера:

.

Определим класс преобразований : , не меняющих это уравнение, то есть нужно посмотреть, при каких условиях преобразование переводит уравнение Шредингера для вектора в уравнение такого же вида только для вектора .

Для этого подействуем на уравнение Шредингера оператором :

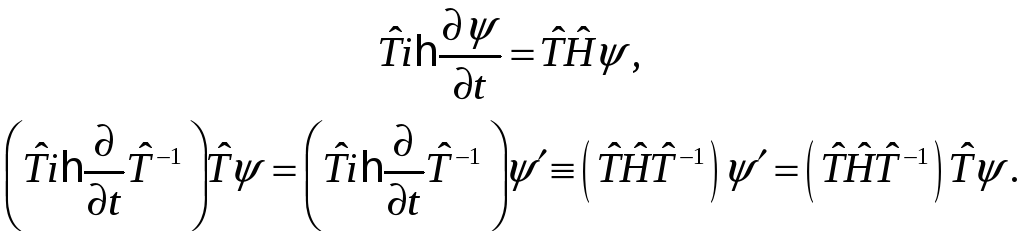
Таким образом, у нас есть два условия (необходимое и достаточное), при выполнении которых преобразование есть преобразование симметрии:

1)

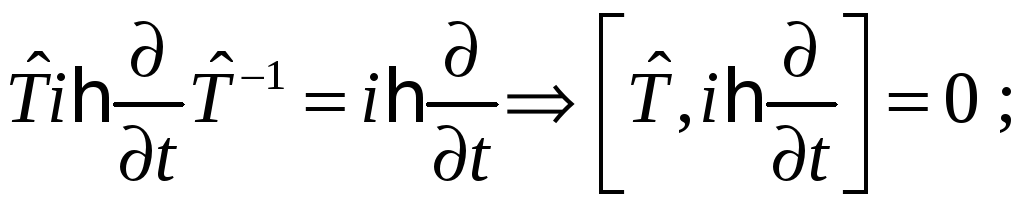
2)

§ 8.2. Микроскопическая обратимость во времени в квантовой механике

Введем оператор обращения во времени, действующий по закону:

.

Вектор комплексный, и мы можем ввести оператор комплексного сопряжения:

.

Запишем новый оператор . И теперь, если к оператору применить необходимое и достаточное условия, то он будет считаться преобразованием симметрии. А отсюда следует, что уравнения движения инвариантны относительно обращения во времени.

Таким образом, все физические величины делятся на два класса: которые меняют знак при обращении времени (например, скорость, импульс) и которые не меняют (например, координата, кинетическая энергия).

§ 8.3. Бесконечно малые преобразования симметрии. Законы сохранения в квантовой механике

Пусть не содержит обращения во времени и является преобразованием симметрии. Представим, что есть сколь угодно малое значение , которое определяет :

,

где - эрмитовский оператор.

Если разложить значение оператора в ряд, то получится:

,

т.е. преобразование отличается от тождественного на бесконечно малую величину. - унитарное преобразование и для него выполняется два условия симметрии, отсюда следует, что – преобразование симметрии.

Рассмотрим теорему.

Теорема: Если имеется сколь угодно малое преобразование симметрии, то имеется сохранение величины .

Доказательство:

.

Имеет место также обратная теорема.

Теорема обратная: Пусть - интеграл движения, тогда мы можем построить унитарный оператор симметрии.

Доказательство:

.

Рассмотрим примеры.

Пусть имеется замкнутая система, в которой интегралами движения являются энергия , обобщенный импульс , момент количества движения . Тогда мы можем сделать вывод о том, что время в системе однородно, а пространство однородно и изотропно.

Покажем это.

1) - интеграл движения и - преобразование симметрии, т.е. однородность во времени;

2) - интеграл движения и - преобразование симметрии, т.е. однородность в пространстве;

3) - интеграл движения и - преобразование симметрии, т.е. изотропность в пространстве.

А теперь рассмотрим, как используется симметрия для решения конкретных задач.