6.2. Операторы физических величин в координатном представлении

Основная проблема квантовой механики - проблема квантования - связана с определением явного вида операторов физических величин.

Пусть некоторая физическая величина изображается линейным эрмитовым оператором , состояние же квантовой системы описывается вектором . В общем случае

, (6.9)

где .

В координатном представлении состояние квантовой системы описывается комплексной функцией координаты x:

  (x), где (x) = (_x,),

  (x), где (x) = (_x, ).

Следовательно, оператор в координатном представлении каждой функции ставит в соответствие функцию :

(6.10)

Если учесть, что каждая физическая величина есть функция канонических переменных, т.е. , где (s - число степеней свободы), тогда согласно принципу соответствия соотношения между физическими величинами и каноническими переменными (координатами и обобщенными импульсами) переносятся на операторы физических величин.

Таким образом, очень важно установить явный вид операторов координат и проекций импульсов . Для этого прежде всего рассмотрим одномерную задачу.

Оператор координаты x в координатном представлении.

Пусть , тогда уравнение (6.9) примет вид:

(6.9`)

В координатном представлении это уравнение преобразуется в согласии с (6.10):

(6.10`)

Разложим векторы  и  в интеграл Фурье по базисным векторам , для которых справедливы уравнения (6.1), и подставим в левую часть уравнения (6.9`):

Тогда уравнение (6.10`) записывается в виде:

откуда

(6.11)

Сравнивая (6.10`) и (6.11), получаем

(6.12)

Следовательно, в координатном представлении оператор координаты есть сама координата , т.е. оператор в координатном представлении есть простая операция умножения на эту координату.

Аналогичным образом можно показать, что

т.е. (6.13)

Оператор в координатном представлении.

Для частицы, движущейся вдоль оси , . Пусть эта физическая величина изображается эрмитовым оператором . Запишем уравнение для собственных векторов и собственных значений этого оператора :

(6.14)

Для конкретного значения импульса это уравнение имеет вид:

(6.14`)

Учтем, что в случае непрерывного спектра собственных значений оператора собственные его векторы нормируются на -функцию Дирака:

(6.15)

Разложим вектор по собственным векторам оператора :

(6.16)

где - проекции собственных векторов , совокупность которых определяет вектор в координатном представлении, т.е. является волновой функцией частицы с заданной величиной импульса. Согласно гипотезе деБройля в качестве такой волновой функции следует взять плоскую монохроматическую волну Таким образом,

. (6.17)

Определим нормировочный коэффициент c, пользуясь условием (6.15):

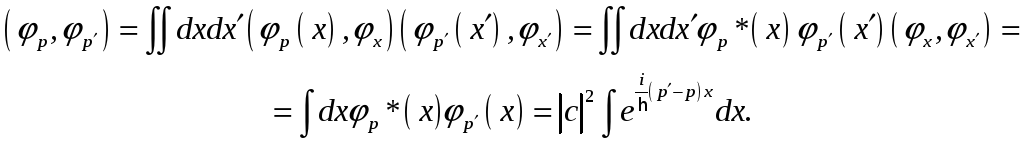
Переходя к новой переменной интегрирования и учитывая определение - функции

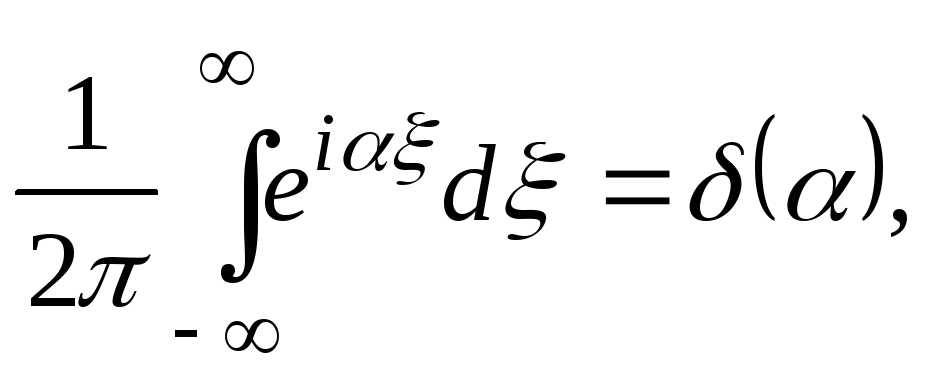(6.18)

для скалярного произведения получим следующий результат:

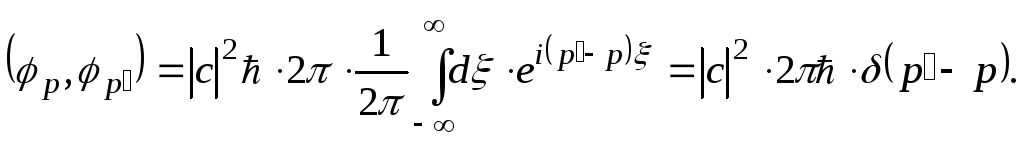
С учетом условия нормировки (6.15) находим:

откуда

(6.19)

Следовательно, нормированная волновая функция частицы (6.19), движущейся вдоль оси с определенным импульсом , имеет вид:

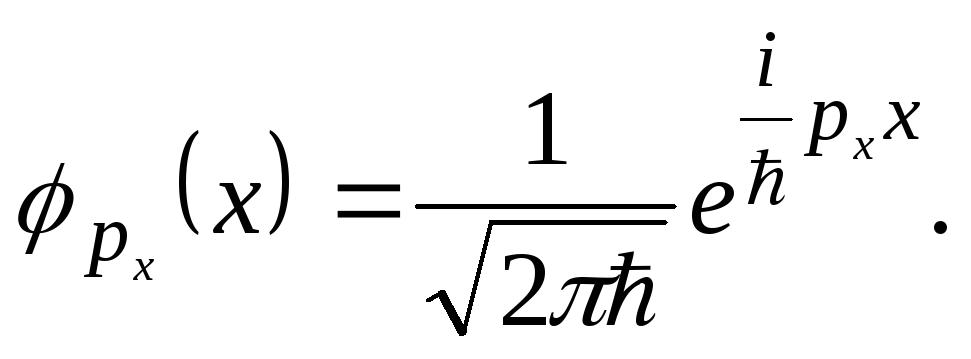¹ (6.20)

Заметим, что

в то же время уравнение (6.14) позволяет записать

Из сравнения левых частей этих уравнений следует выражение для оператора в координатном представлении

. (6.21)

Правильный явный вид оператора в координатном представлении (6.21) подтверждают расчеты с произвольным вектором квантового состояния системы. Разложим для этого по собственным векторам оператора , а затем по собственным векторам оператора :

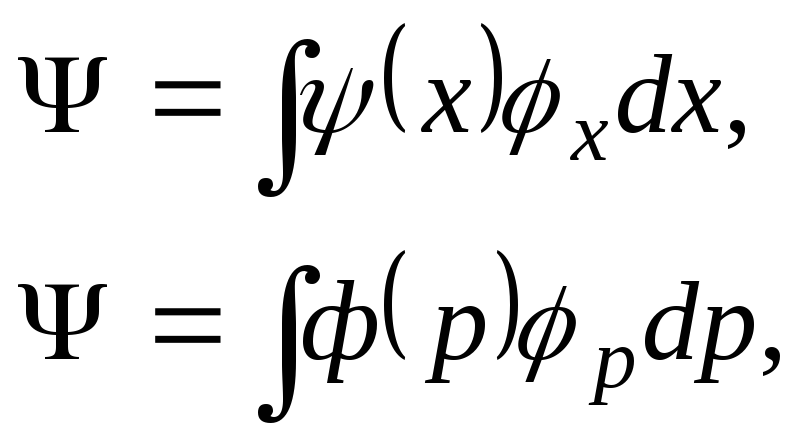
где - плотность вероятности обнаружения у частицы координаты , - плотность вероятности обнаружения у частицы импульса .

Тогда волновая функция с учетом (6.17) может быть представлена в виде:

(6.22)

Действуя оператором на волновую функцию , получим:

.

Зная явный вид оператора проекций импульса в координатном представлении, подобным образом можно доказать справедливость аналогичных выражений для операторов , т.е.

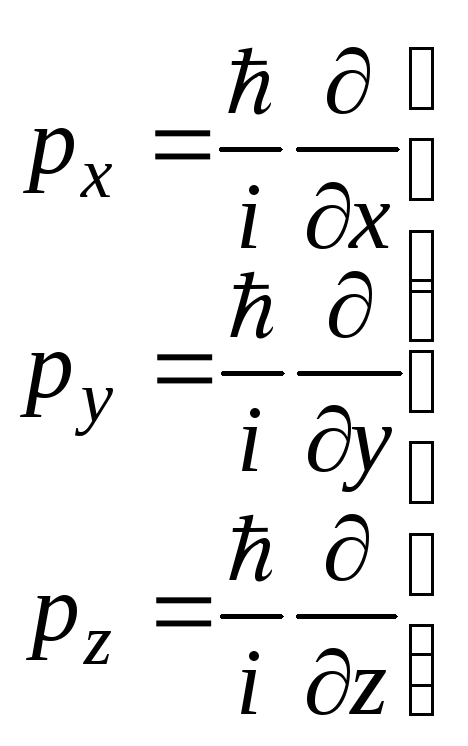
. (6.23)