§1. Идея о дискретности значений физических величин

1.1. Классическая теория равновесного излучения

Первая проблема связана с теоретическим обоснованием равновесного излучения, возникающего внутри полости, окруженной со всех сторон непроницаемыми стенками, нагретыми до некоторой температуры (рис.1.1). Следует заметить, что небольшое отверстие, сделанное в стенке такой полости, можно рассматривать как абсолютно черное тело (Вин и Луммер, 1895г.)

Рис. 1.1.

Универсальность законов термодинамики обеспечивает применимость их как к веществу, так и к полю ( как к классическим, так и к квантовым системам). В применении к равновесному излучению термодинамика позволила установить следующее :

1. Закон Кирхгофа, согласно которому отношение лучеиспускательной способности тела, к его поглотительной способности при данной температуре, не зависят от физических свойств тела и равно лучеиспускательной способности абсолютно черного тела, т.е. является универсальной функцией температуры 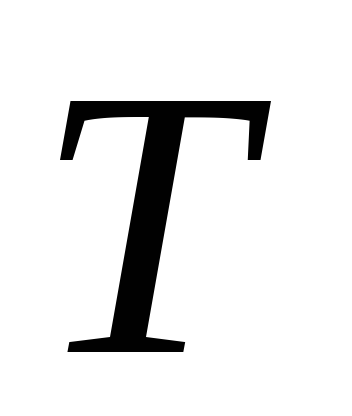и частоты (1859г.).

2. Существование светового давления 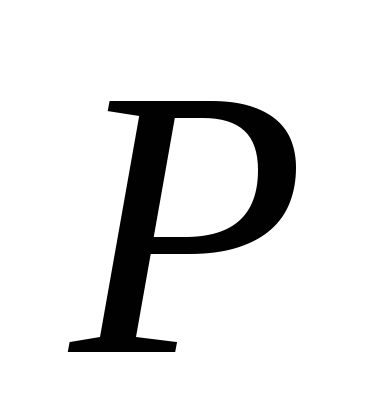излучения (величину светового давления легко найти, исходя из законов электродинамики: 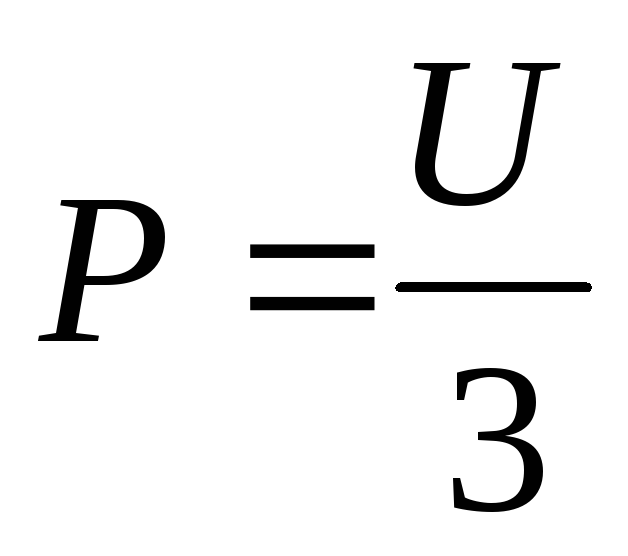, где 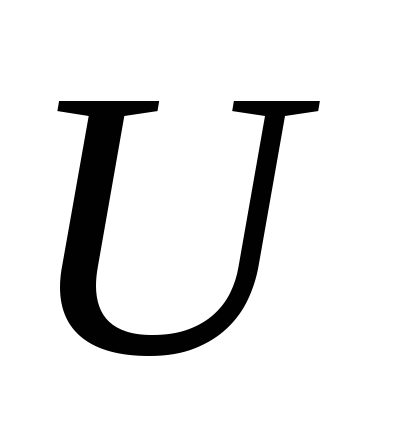– плотность энергии излучения).

3. Закон Стефана – Больцмана¹ о зависимости плотности энергии от температуры:

, (1.1)

отсюда на основе опытных данных для температуры и плотности энергии равновесного излучения вычисляют постоянную ².

4. Закон Вина о спектральной плотности 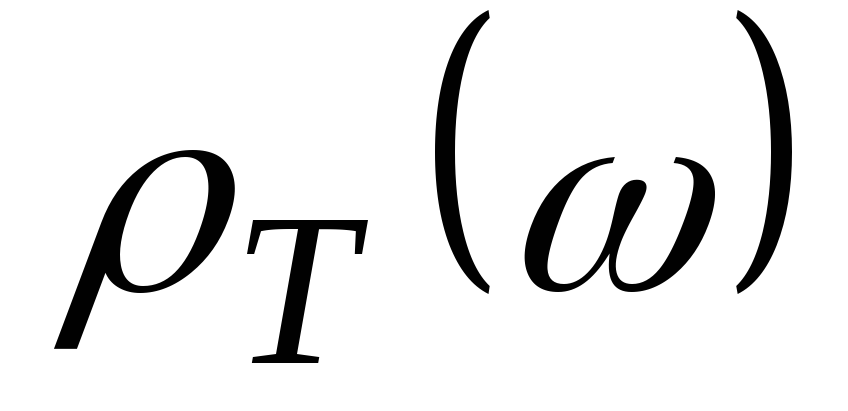равновесного излучения:

, (1.2)

вид функции остается термодинамически неопределенным.

5. Закон смещения Вина о том, что длина волны, соответствующая максимальной спектральной плотности энергии равновесного (черного) излучения, обратно пропорциональна абсолютной температуре:

, (1.3)

где - постоянная Вина.

Закон Вина (1.2) позволяет по заданной кривой распределения спектральной плотности энергии, при какой – либо температуре построить аналогичную кривую при любой другой температуре (рис. 1.2).

Формула Вина (1.2) автоматически приводит к закону Стефана – Больцмана (1.1):

,

Вводя новую переменную , получим:

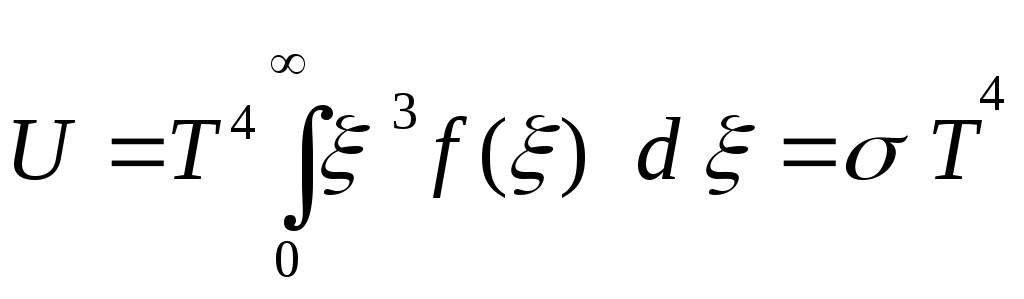. (1.1’)

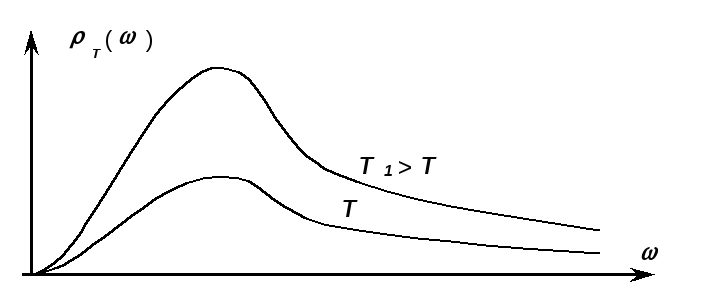
Рис. 1.2.

Таким образом, задача определения универсальной функции, с которой связанно теоретическое обоснование законов равновесного излучения, вышла на первое место в физике.

В классической физике эта задача решалась следующим образом. В полости кубической формы с ребром существуют колебания всевозможных частот. В состоянии динамического равновесия колебания представляют суперпозицию стоячих волн. В декартовой системе координат, оси которой направлены вдоль трех ребер куба (рис. 1.3), условия существования стоячих волн записываются в виде:

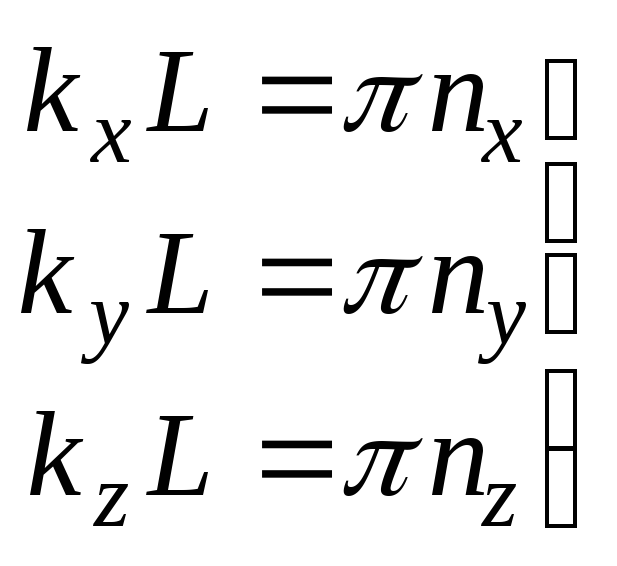, (1.4)

где – целые положительные числа.

Тогда число стоячих волн , волновые числа которых заключены в интервале , равно числу целых чисел в объеме , т.е.

. (1.5)

Переходя к сферическим координатам, где элементарный кубик (рис. 1.3) будет представлен элементарным объемом сферического слоя радиуса и толщины в первом октанте (из-за целых положительных значений чисел ), число стоячих волн в полости объема перепишется в виде:

. (1.6)

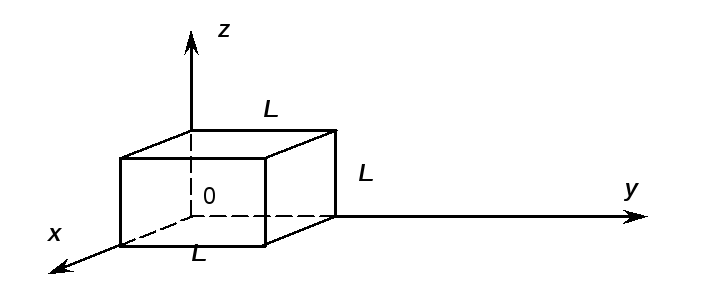
Рис. 1.3.

Подставляя соотношение в формулу (1.6.), получим для числа колебаний с частотой из интервала в объеме полости формулу:

. (1.7)

Вейлем было показано, что это выражение справедливо независимо от формы полости и природы волн. Полное число электромагнитных колебаний следует увеличить в 2 раза за счет существования двух независимых поляризаций у поперечных волн:

. (1.8)

В первоначальных теориях число частот w из интервала , даваемое формулой Вейля (1.8), рассматривали как число осцилляторов оболочки полости, посылающих электромагнитные волны в полость объема .

Пользуясь этим представлением и рассчитав среднюю энергию линейного гармонического осциллятора на основе законов классической статистической физики, а именно, теоремы о равномерном распределении энергии по степеням свободы:

. (1.9)

Релей и Джинс получили формулу для энергии излучения, с частотой , в полости в виде:

. (1.10)

Отсюда следует выражение:

, (1.11)

называемое формулой Релея – Джинса. Она удовлетворяет термодинамическому закону Вина (1.2), но резко противоречит эксперименту и закону Стефана – Больцмана. Действительно, плотность энергии равновесного излучения , но не .

Этот результат настолько противоречил эксперименту, что получил название «ультрафиолетовой катастрофы» (Эренфест, см. рис 1.4.)

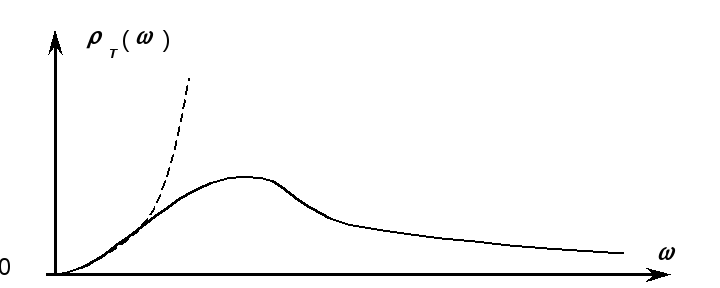
Рис. 1.4.

Возможен и другой подход к выводу формулы для в рамках классических представлений. Число колебаний с частотой , являющиеся носителями определенной энергии , дается распределением Больцмана:

, (1.12)

где – полное число носителей энергии. Отсюда для средней энергии колебаний с частотой оказывается равным

, (1.13)

следовательно,

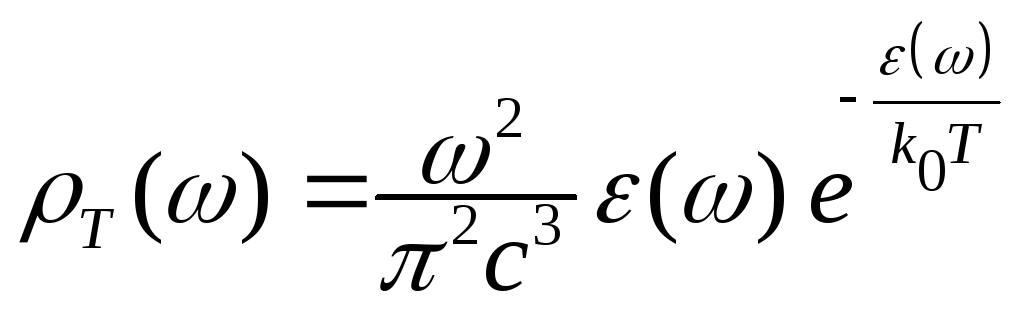, (1.14)

Вин на основе общих термодинамических соображений показал, что , где - коэффициент пропорциональности. Тогда формула Вина принимает вид:

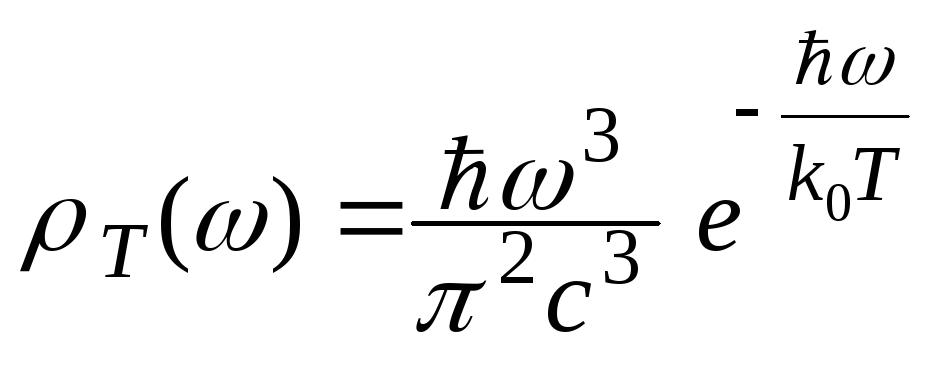. (1.15)

Этот закон Вина выполняется хорошо лишь для достаточно больших частот излучения.

Таким образом, формулы Релея – Джинса и Вина описывались лишь концы спектра равновесного излучения (абсолютно черного тела).

Нужны были новые идеи для создания более общей и строгой теории, объясняющей законы равновесного излучения (1.1), (1.2), (1.3) и разрешающей проблему с «ультрафиолетовой катастрофой».