Тема: «Вычисление определенных интегралов»

Цель работы: изучение методов вычисления определенных интегралов, оценка точности этих методов. Получение практических навыков программной реализации методов вычисления определенных интегралов.

Технические средства: IBM PS AT.

Программное средство: Visual Studio или Delphi

Теоретические сведения

При решении многих физических и геометрических задач приходится искать неизвестную функцию по дан­но­му соотношению между неизвестной функцией, ее про­из­вод­ными и независимыми переменными. Такое со­от­но­ше­ние называется дифференциальным урав­не­ни­ем, а отыс­ка­ние функции, удовлетворяющей урав­не­нию, называется ре­шением или интегрированием дан­но­го уравнения.

Простейшее дифференциальное урав­не­н­ие первого по­ряд­ка у' = f(у, t) имеет семейство решений у = у(t), яв­­­ля­ю­щи­х­ся интегральными кривыми второго по­ряд­ка, ча­­ще все­­го ви­да у = Се^t, с произвольной по­сто­ян­­ной С. Тог­­­да вы­бор начального значения у(0)=у₀ опре­де­ля­ет од­ну из кри­­вых семейства ре­ше­ний, ко­то­рая и будет счи­таться ре­ше­нием по­став­ленной за­да­чи.

Основной считается задача Коши в раз­де­ле высшей ма­те­ма­тики "решение дифференциальных уравнений при­бли­жен­ными методами", формулирующаяся тра­ди­ци­он­но так: тре­бу­ет­ся найти решение ура­вне­ния у' = f(у, t) в виде у = у(t), удов­­лет­во­ря­ю­щее на­чаль­ному условию у(0) = у₀^. Иными сло­ва­­­ми, тре­буется найти среди се­мейства ин­тег­раль­ных кри­вых, являющихся част­ными решениями диф­фе­ренциального урав­не­ния у' = f(у, t), интегральную кри­вую у(t), которая про­хо­­дит через заданную точ­ку М(t₀, у₀).

Для двумерного случая задача Коши фо­р­му­ли­ру­ется так: если f(х,у) непрерывна в некоторой об­лас­ти R, оп­ределенной как |х - х₀| < а; |у - у₀| < b, то существует, по крайней мере, одно решение у = у (х, t), определенное в ок­рестности |х - х₀| < h, где h > 0, и это решение будет единственным, если вы­пол­няется условие Липшица

|f(х,) - f(х,у)| < N ^. | у|,

где N - некоторая константа Липшица, зависящая в об­щем случае от а и b.

Заметим, что решение системы диф­фе­рен­ци­аль­ных урав­нений первого порядка

при условии, что производные df/dу, df/dх, dg/dу и dg/dх су­­­щест­ву­ют на каждом интервале ин­те­гри­ро­ва­ния, со­дер­жит уже две постоянные ин­те­г­ри­ро­ва­ния и, сле­­до­ва­тель­но, нуж­ны два начальных ус­ло­вия, чтобы од­­но­знач­но оп­ре­де­лить эти кон­стан­ты.

Как правило, аналитическими методами можно ре­шить диф­ференциальные уравнения только опре­де­лен­но­го вида. Если уравнение не сводится никакими тож­дес­твенными пре­образованиями ни к одному из из­вест­ных типов диф­фе­рен­циальных уравнений, то решение та­­кой задачи может быть найдено только спе­ци­аль­ны­ми численными ме­то­да­ми. Рассмотрим на­и­бо­лее часто при­меняемые на практике.

Приближенное решение обыкновенного дифференциального уравнения методом Эйлера.

При обсуждении методов решения задачи Ко­ши огра­ничимся рассмотрением диф­фе­рен­ци­аль­но­­го урав­не­ния пер­вого порядка у' = f(х,у), удов­лет­воряющего на­чальному ус­ловию у(х₀) = у₀ .

Численное решение задачи состоит в по­стро­е­нии таб­ли­­цы приближенных значений у₁, у₂, ..., у_n, яв­ля­ю­щих­ся ре­ше­­ниями уравнения у = у(х) в то­чках х₁, х₂, ..., х_n. Чаще все­го точки х_i рас­по­ло­же­ны равномерно: х_i = х₀ + h^.i, где i = =1, 2, ..., n. Точ­ки х_i называют узлами сетки, h - шагом сет­­­ки. Ясно, что h > 0.

Для получения решения задачи Коши вос­поль­зуемся раз­­ложением функции в ряд Тейлора. Для этого про­диф­фе­ре­н­цируем исходное урав­не­ние у' = f(х,у) по х n раз. Тог­да с учетом пра­вила диф­фе­рен­ци­ро­ва­ния слож­ной функ­ции по­­лучим сле­дующие соотношения:

у" = f_x (х, у) + f_x (х, у)  у';

у"'= f_xx (х,у)+2f_xy(х,у)  у' + f_yy(х,у)  (у') + f_y(х,у)  у"; . . .

Полагая х = х₀ и у = у₀, получаем ряд у'(х₀); у"(х₀); у"'(х₀); ... ; у⁽ⁿ⁾(х₀), который сходится к ре­ше­нию по­став­лен­ной задачи, т.е.

. (4.1)

Надо заметить, что если |х - х₀| больше ра­ди­у­са схо­ди­мос­ти ряда у'(х₀); у"(х₀); у"'(х₀); ...; у⁽ⁿ⁾(х₀), то погрешность | - у| не стремится к ну­лю при n , т.е. ряд рас­хо­дит­ся. Тогда по­сту­па­ют сле­дующим об­ра­зом. Отрезок [х₀,х₀+Х], на ко­то­ром ряд расходится, раз­би­ва­ют на меньшие от­рез­­ки [х_i, х_i+1], где i = 1, 2, ..., n, и по­лу­чают но­вые по­сле­до­ва­тельные приближения у_j к ре­шению у(х_j ) при j = 1, 2, ..., m, используя следующую схему:

1) у_i считаем найденным (для первого шага им мо­жет быть у₀);

2) вычисляем в точке х_i производные у_i^(k);

3) полагаем ;

4) считаем у_i+1 = z_i(х_i+1);

5) повторяем с первого пункта.

Если же в формуле (4.1) положить n=1, то по­лу­чим ос­нов­ную расчетную формулу метода Эй­ле­ра: у_i+1=у_i+h f(х,у).

Этот метод относится к группе одношаговых, в ко­то­­­рых для расчета точки (х_i+1, у_i+1) тре­буется ин­фор­ма­ция только о последней вы­чис­лен­ной точке (х_i, у_i). Он до­­пус­ка­ет простую геометрическую ин­терпретацию. По­лу­ча­ет­ся, что на каждом новом при­ближении ре­шение пе­ре­ходит на другую кривую из семейства ре­ше­ний. Этот факт для не­ко­то­рых диф­фе­рен­ци­аль­ных урав­не­ний может привести к боль­шим ошиб­кам и решения за­да­чи Коши начнет рас­хо­диться. Заметим, что хотя метод Эй­ле­ра относится к ит­­е­ра­ци­он­ным, но ошибки, сделанные на ран­­них эта­пах, не умень­шаются из-за не­ус­той­­­чи­вос­ти вы­чис­лительной схемы и ее чув­ст­ви­тель­нос­ти к шаг­у раз­би­е­ния отрезка, на котором ищется ре­ше­ние. Что­бы обойти эту трудность, при­­меняют дру­гие вы­­чис­ли­тель­ные схемы или ме­то­­ды.

Для оценки погрешности метода Эйлера на од­­ном из ша­гов сетки разложим точное решение в ряд Те­й­­лора в окрестности узла х_i:

у(х_i+1) = у(х_i+h) = у(х_i) + у'(х_i)^.h + (h²) =

= у(х_i) + f(х_i,у_i)^.h + (h²).

Сравнение разложения с основной расчетной фор­му­лой метода показывает, что они совпадают до чле­нов первого порядка по h, а погрешность фор­мулы рав­на (h²), т.е. метод Эйлера от­но­сит­ся к методам пер­во­го порядка.

Формальные параметры про­цедуры. Входные: х (тип real) - очередное значение х_i; h (тип real) - величина ша­га разбиения отрезка, на котором ищется решение; у (тип real) - предыдущее значение у_i; FUNC(х) (тип real) - процедура-функция, вычисляющая значение пра­­вой час­ти уравнения по заданным х и у. Ре­зуль­татом ра­бо­ты данной процедуры-функции явит­ся очередное зна­че­ние у_i+1.

Приближенное решение обыкновенного дифференциального уравнения методом Эйлера с уточнением

Метод Эйлера относится к ме­то­дам первого по­ряд­ка, потому что обладает не толь­ко не­у­стой­чи­вос­тью решения, но и низкой точ­ностью. Однако в смысле по­грешности он да­ет удовлетворительные результаты даже при не очень больших h. К сожалению, ошиб­ки при вы­чис­лении накапливаются от шага к шагу, и к кон­­цу от­резка решение содержит значительные по­греш­­нос­ти. Заметим также, что источником оши­бок очень часто являются и исходные данные. Су­щест­вуют, од­нако, методы, позволяющие ис­поль­зо­вать все до­сто­ин­ства метода Эйлера и од­но­вре­мен­но по­­вышающие точность вычислений.

Рассмотрим основную расчетную формулу ме­то­­да Эй­ле­ра: у_i+1 = у_i+ h^.f(х,у). Одна из мо­дификаций ме­­то­да за­ключается в том, что сна­чала вычисляют про­­ме­жу­точ­ные значения

х_i+1/2 = х_i + h/2 и у_i+1/2 = у_i + f_i ^. h/2

и находят направление поля интегральных кривых в сред­­­ней точке (х_i+1/2, у_i+1/2 ) отрезка [х_i, х_i+1], т.е.

f_i+1/2 = f(х _i+1/2, у _i+1/2),

а затем полагают у_i+1 = у_i+1/2 + f_i ^. h/2.

Другой модификацией этого же метода яв­ля­ет­ся не­ли­нейная вычислительная схема: зная пре­ды­дущее зна­че­ние у_i, вычисляют у ^~_i+1 как у ^~_i+1 = у_i + h у_i , а затем опре­деляют поправку к ре­ше­нию  у ^~ _i+1 по формуле  у ^~_i+1 = f(х_i+1, у_i+1) . Решение находится из уравнения

у_i+1 = у_i + h/2^. [ f(х_i,у_i) +  у ^~_i+1 ] .

Эту вычислительную схему еще называют методом Эйлера - Ко­ши.

Другая вычислительная схема, которую называют ме­­тодом Эйлера с упорядочением решения, заключается в том, что каждое значение у_i+1 = у(х_i+1), где у(х) - ис­ко­мое решение, а х _i+1 = х₀ + h^. (I+1), i = 0, 1, ..., N, оп­ре­де­ля­ется по сле­ду­ю­щей схеме:

1) за начальное приближение берется

,

2) найденное значение уточняется по формуле

, где i = 1, 2, ..., N;

3) уточнение продолжают до тех пор, пока в пре­де­лах тре­буемой точности (заранее заданной) два по­сле­до­ва­тель­ных приближения не совпадут, т.е.

,

где - погрешность или любое малое число. После этого полагают у_k+1 = у_k+1^-(i), где у_k+1^-(i) общая часть по­лу­чен­но­го ряда ре­шений у_k+1⁽ⁱ⁾.

Иногда описанная выше схема называется ме­то­дом Эйлера с итерационным уточнением ре­ше­ния.

Если после трех итераций решения в пределах тре­бу­е­мой погрешности не совпали, то следует либо умень­шить шаг, либо увеличить погрешность.

Приближенное решение обыкновенного дифференциального уравнения методом Адамса

Если дифференциальное уравнение у'= f(х, у) име­­ет в правой части сложное ана­ли­ти­чес­кое вы­ра­же­ние, то тог­­да применяют экст­ра­по­ля­ционный ме­тод Адамса, ко­то­рый не требует мно­го­крат­но­го подсчета правой час­ти.

Пусть для дифференциального уравнения зада­ны на­­чаль­ные условия х = х₀ , у = у₀. Требуется най­ти ре­ше­­ние уравнения у' = f(х, у) на отрезке [а, b].

Разобьем отрезок [а, b] равномерно на n частей точ­ка­­­ми х_i = х₀ + h^.i, i = 0, 1, ..., n, h = (b - а)/n. Выберем про­­из­воль­но элементарный отрезок, на котором про­ин­тегрируем диф­ференциальное уравнение

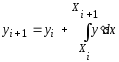_или .

Для нахождения производной воспользуемся вто­рой ин­терполяционной формулой Ньютона, ог­ра­ни­чив­шись разностями третьего порядка с уче­том t = (х - х_i)/h:

Подставим полученное выражение для у' в ин­те­­граль­ное уравнение и, учитывая, что dх = hdt, име­ем

Обозначим через q_i = у_i'; h = f(х_i, у_i)^.h, , тог­да для любой разности ^m q_i = ^m (у_i'h) имеем вы­ражение

y_i = q_i + 1/2 ^. q_i-1 + 5/12 ^. ²q_i-2 + 3/8 ^. ³q_i-3,

используемое для получения решения урав­нения

у_i+1 = у_i + у_i.

Две по­­след­ние формулы яв­ля­ют­ся основными в эк­стра­по­ля­ци­он­ном методе Адам­са.

Для начала процесса вычисления нужны четыре на­чаль­ных значения у₀, у₁, у₂ и у_3, которые мож­но опре­де­лить любым известным методом. Далее, зная у₀, у₁, у₂ и у₃ , находят q₀ = =hy₀’ = h f(x₀, y₀); q₂ = hy₂’ = h f(x₂, y₂); q₃ = hy₃’ =h f(x₃, y₃); q₄ = hy₄’ = h f(x₄, y₄) и составляют таблицу конечных раз­нос­тей ве­личин q.

Таблица 4.1

№ п/п	xi	yi	yi	yi’=f(x0,y0)	qi = hyi’	Конечные разности
0	x0	y0		f(x0,y0)	—	—	—	—
1	x1	y1		f(x1,y1)	q0	q0	2q0	3q0
2	x2	y2		f(x2,y2)	q1	q1	2q1
3	x3	y3	y3	f(x3,y3)	q2	q2
4	x4	y4		f(x4,y4)	q3
5	x4	y5		...	...
...	...	...

Метод Адамса заключается в продолжении дан­ной таб­ли­цы разностей с помощью формулы для у_i. Ис­поль­зуя уже вычисленные q₃, q₂, ^q₁ и ^q₀, рас­по­ло­жен­ные в таб­­лице диагонально, по формуле для у_i по­лу­чают, по­ла­гая n = 3,

у₃ = q₃ + 0.5q₂ + (5/12) ^. ^q₁ + (3/8) ^. ^q₀ ,

у₃ вносят в таблицу и находят у₄ = у₃+у₃. Затем, ис­поль­зуя х₄ и у₄ находят f(х₄,у₄), q₄, q₃, ^q₂ и ^q₁, т.е. новую ди­­а­го­наль. По этим данным опре­деляют значение у₄, ко­то­рое тут же вно­сят в таб­ли­цу, и находят у₅ = у₄ + у₄.

Таблицу продолжают по описанному алгоритму до ее за­пол­­не­ния, вычисляя правую часть формулы при этом толь­ко один раз. Что­бы оценить погрешность по­лу­­чен­но­го результата, можно применить правило Рун­­ге или просто следить за третьими разностями ^q_i, ко­то­рые считаются по­сто­ян­ны­ми. Этого мож­но добиться, вы­­бирая h каждый раз та­кой, что­­бы выражение для оценки погрешности бы­ло |³q_i-1 - ³q_i| < . На практике h выбирают из не­ра­вен­ст­ва h⁴ < , где - за­данная точность ре­ше­ния.

Метод Рунге состоит в том, что сначала находится ре­шение диф­фе­рен­ци­аль­но­го уравнения при шаге h, а за­тем зна­че­ние h удва­и­ва­ет­ся и находится решение при но­­вом шаге. Погрешность оце­нивается по формуле

= (2^m - 1) ^. |y_n^~ - y^~_2n| ,

где y_n^~ - значение приближенного вычисления при двойном шаге; m - порядок метода.

Формальные параметры процедуры. Входные: а, b (тип real) - начало и конец от­резка, на котором ищут ре­ше­ние; h (тип real) - шаг раз­би­е­ния отрезка [а, b]; ЕРS (тип re­al) - заранее заданное ма­лое число (используется для оп­ре­­деления первых че­ты­рех значений у_i методом Эйлера с уточ­­не­ни­ем); у_N - начальное у₀. Перед началом работы сле­ду­ет определить процедуру-функ­цию, по ко­то­рой вы­чис­ля­ют правую часть диф­фе­рен­ци­аль­ного урав­не­ния f (х, у). Вы­ходные: массив уi (тип real) зна­че­ний у_i, най­денных ме­то­­дом Адамса.

Приближенное решение обыкновенного дифференциального уравнения методом Рунге - Кутта

Методы Рунге - Кутта образуют се­мей­ство ме­то­дов ре­ше­­­ния задачи Коши. Oни от­носятся к мно­го­шаговым ме­то­дам повышенной точ­ности (от второго по­рядка и выше). Здесь бу­дет рассмотрен одношаговый метод Рунге - Кут­та чет­­вертого порядка точности. За­ме­тим по­пут­но, что ме­то­ды Рунге - Кутта отличаются от раз­нос­тных тем, что все они допускают вычисление функ­­ции не только в заранее за­­данных узлах сет­ки, но и в некоторых промежуточных точ­­ках, тем са­мым по­зво­ляя уменьшать шаг вычислений во вре­мя самого про­цесса построения решетки.

Итак, пусть требуется найти решение диф­фе­рен­ци­аль­но­го уравнения у' = f(х, у), удов­лет­во­ря­ю­щего на­чаль­ному ус­ловию у(х₀) = у₀ .

Численное решение задачи состоит в по­стро­е­нии таб­ли­­цы приближенных значений у₀, у₁, ..., у_n решения урав­не­ния у' = f(х,у) в точках х₀, х₁, ..., х_n, которые на­зы­вают уз­ла­ми сетки. Для крат­кос­ти обозначим х_i = х₀+ ih; у_i = у(х_i), где h - шаг сет­ки (ясно, что h > 0).

Обычно методом Рунге-Кутта в литературе на­зы­ва­ют ме­­тод, согласно которому у искомой функ­ции вы­чис­ляют по формулам:

у_i+1 = у_i + /6,

где обозначено:

 = k₁+2k₂ +2k₃ +k₄ ; k₁ = hf(x_i, y_i);

k₂ = h f(x_i + h/2 ,y_i + k₁/2); k₃ = h f(x_i + h/2 ,y_i + k₂/2);

k₄ = h f(x_i + h ,y_i + hk₃).

Погрешность метода на одном шаге сетки равна М^.h⁵ , где М - некоторое число. Но на прак­ти­ке даже при­бли­жен­но очень трудно оценить М, поэтому при оцен­ке по­греш­нос­ти используют пра­вило Рунге. Для че­го сначала про­во­дят вы­чис­ле­ния с шагом h, а затем пов­торяют их с числом h/2. Если у_i^(h) - приближение, вы­чис­ленное с ша­гом h, а у_i^(h/2) - с шагом h/2, то спра­вед­ли­ва оце­нка

.

Формальные па­ра­мет­ры процедуры. Входные: N (тип in­te­ger) - количество раз­би­е­ний отрезка [а, b]; Х, Y (тип re­al) - на­чаль­ные значения, со­от­вет­ствующие x₀ и y₀; h (тип re­al) - шаг ин­те­гри­рования системы; FUNС - имя про­це­­ду­ры-функции, по ко­то­рой вы­чис­ля­ют зна­че­ния пра­­вой час­­ти урав­нения у' = f(х, у). Вы­­ходные: YR (тип re­al) - мас­сив, со­дер­жа­­щий ре­шения сис­те­мы в точках х_i = х₀ + hi.

Задание

Написать программу для интегрирования обыкновенного дифференциального уравнения (методы задаются преподавателем).

Варианты

1. ,

2. ,

3. ,

4. ,

5. ,

6. ,

7. ,

8. ,

9. ,

10. ,

Требования к программе

1. Программа должна быть написана в среде Visual Studio или Delphi.

2. В программе должно быть предусмотрено следующее:

ввод исходных данных и вывод результата в удобной для пользователя форме;

возможность пошагового просмотра решения задачи;

справка с комментариями по работе с программой;

корректировка исходных данных;

сохранение исходных данных и результата в файле.

Порядок выполнения работы

1. Получить задание у преподавателя.

2. Разработать алгоритм решения задачи.

3. Реализовать полученный алгоритм.

4. Проанализировать результаты работы алгоритма.

5. Оформить отчет по лабораторной работе.

Содержание отчета

1. Номер и тема лабораторной работы.

2. Цель выполнения работы.

3. Описание алгоритма.

4. Руководство пользователю.

5. Пример работы программы.

6. Анализ полученных результатов и вывод по работе.

7. Текст программы с комментариями привести в приложении.

Библиографический список

1. Белашов В.Ю., Чернова Н.М. Эффективные алгоритмы и программы вы­чис­ли­тель­ной математики. Магадан: СВКНИИ ДВО РАН, 1997. 160 с.

2. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высш. шк., 1994. - 544 с.

3. Турчак Л.И. Основы численных методов. М.: Наука, 1987. – 320 с.

4. Демидович Б.Н., Марон И.А. Основы вычислительной математики. М.: Высш. шк., 1994. - 172 с.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению лабораторных работ

по дисциплине «Вычислительная математика»

для студентов специальностей