Лабораторная работа № 1
Тема: «Прямые и итерационные методы решения систем линейных уравнений»
Цель работы: изучение методов решения линейных уравнений, оценка и сравнение этих методов. Получение практических навыков программной реализации методов решения систем линейных уравнений.
Технические средства: IBM PS AT.
Программное средство: Delphi или Visual Studio
Теоретические сведения
Система m линейных алгебраических уравнений с n неизвестными в общем виде может быть записана следующим образом:
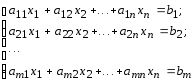(1.1)
или в матричном
виде AX = B, где A
- прямоугольная матрица
размерности mn,
X - вектор n-го порядка,
B - вектор m-го порядка.
Решением системы (1)
называется такая упорядоченная
совокупность чисел
которая обращает все уравнения
системы в верные равенства.
Две системы называются эквивалентными
(равносильными),
если множества их решений
совпадают.
Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной - в противном случае. Совместная система называется определенной, если она имеет единственное решение, и неопределенной - в противном случае. Система является определенной, если rang A = rang B, где матрица B, полученная из матрицы A добавлением столбца свободных членов, называется расширенной.
Если матрица A - квадратная и det A 0, то она называется неособенной (невырожденной), при этом система уравнений, имеющая неособенную матрицу A, совместна и имеет единственное решение.
Eсли уравнения (1) являются нелинейными относительно неизвестного вектора Х, то соответствующая система, записанная в векторной форме
(1.2)
называется системой нелинейных уравнений. Она может быть также представлена в координатном виде:
1 < k < n.
Многообразие численных методов решения систем линейных алгебраических уравнений можно разделить на два класса: прямые (или точные) и итерационные (или приближенные) методы. В лабораторной работе рассматриваются эффективные алгоритмы, реализующие ряд методов из обоих классов.
Метод исключения Гаусса для систем линейных уравнений
Из курса линейной алгебры известно, что решение системы линейных уравнений можно просто найти по правилу Крамера - через отношение определителей. Но этот способ не очень удобен для решения систем уравнений с числом неизвестных > 5, т.е. когда найти определитель сложно, а при числе неизвестных > 10 нахождение определителя с достаточно высокой степенью точности становится самостоятельной вычислительной задачей. В этих случаях применяют иные методы решения, среди которых самым распространенным является метод Гаусса.
Запишем систему линейных уравнений (1.1) в виде
(1.3)
Если матрица системы верхняя треугольная, т.е. ее элементы ниже главной диагонали равны нулю, то все хj можно найти последовательно, начиная с хn, по формуле
.
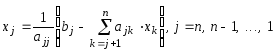(1.4)
При j > k и аjj 0 этот метод дает возможность найти решение системы.
Метод Гаусса для произвольной системы (1.1) основан на приведении матрицы А системы к верхней или нижней треугольной. Для этого вычитают из второго уравнения системы первое, умноженное на такое число, при котором а21 = 0, т.е. коэффициент при х1 во второй строке должен быть равен нулю. Затем таким же образом исключают последовательно а31 , а41 , ..., аm1 . После завершения вычислений все элементы первого столбца, кроме а11, будут равны нулю.
Продолжая этот процесс, исключают из матрицы А все коэффициенты аij, лежащие ниже главной диагонали.
Построим общие формулы этого процесса. Пусть исключены коэффициенты из k - 1 столбца. Тогда ниже главной диагонали должны остаться уравнения с ненулевыми элементами:
Умножим k-ю строку на число
и вычтем ее из m-й строки. Первый ненулевой элемент этой строки обратится в нуль, а остальные изменятся по формулам
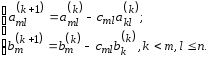(1.5)
Произведя вычисления по формулам (1.5) при всех указанных индексах, исключим элементы k-го столбца. Такое исключение назовем циклом, а выполнение всех циклов назовем прямым ходом исключения.
После выполнения всех циклов получим верхнюю треугольную матрицу А системы (1.3), которая легко решается обратным ходом по формулам (1.4). Если при прямом ходе коэффициент аjj оказался равен нулю, то перестановкой строк перемещаем на главную диагональ ненулевой элемент и продолжаем расчет.
Формальные параметры процедуры. Входные: n (тип integer) - порядок системы; а (тип real) - массив коэффициентов системы размером nn; b (тип real) - массив-строка свободных членов. Выходные: х (тип real) - массив-строка, в который помещается решение системы.