1.Кинематическое описание движения частицы. Скорость и ускорение.

Кинематика занимается описанием движения, отвлекаясь от его причин. Для описания движения можно выбирать различные системы отсчета. В различных системах отсчета движение одного и того же тела выглядит по разному. Простейшим объектом, движение которого изучает классическая механика, является материальная точка. Материальной точкой называется макроскопическое тело, размеры которого настолько малы, что в рассматриваемом движении их можно не принимать во внимание и считать, что все вещество тела как бы сосредоточено в одной геометрической точке.

2. Нормальное и тангенциальное ускорение.

Ускоре́ние (обычно обозначается , в теоретической механике ) — производная скорости по времени, векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).

Тангенциальное ускорение —  направлено по касательной к траектории (обозначается иногда  и т.д., в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.

Центростремительное или Нормальное ускорение  — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда  итд). Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:

3. Поступательное и вращательное движение твердого тела

ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

В твердом теле скорости точек распределяются таким образом, что проекции скоростей двух точек на прямую, их соединяющую, равны между собой (кинематическое определение твердого тела).

Положение твердого тела в общем случае определяется шестью параметрами; в частных случаях, когда на движение тела наложены ограничения, число параметров соответственно уменьшается.

Поступательным движением твердого тела называется такое его движение, при котором всякая прямая, неизменно связанная с телом, перемещается параллельно самой себе. Для этого достаточно, чтобы две непараллельные прямые, связанные с телом, перемещались параллельно самим себе. При поступательном движении все точки тела описывают одинаковые, параллельно расположенные траектории и имеют в любой момент времени одинаковые скорости и ускорения. Таким образом, поступательное движение тела определяется движением одной его точки О.

Вращательное движение твердого тела

Момент количества движения твердого тела относительно оси вращения, oсь вращения обозначена z:

Дифференциальное уравнение вращения твердого тела относительно неподвижной оси

где N^e - момент внешних сил, приложенных к твердому телу, относительно оси вращения.

Изменение угловой скорости тела за конечный промежуток времени

где N(S^e) - момент импульса внешних сил относительно оси вращения.

4. Угловая скорость и угловое ускорение

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени: Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ (рис. 2). Размерность угловой скорости dim ω = Т^-1, а ее единица — радиан в секунду (рад/с). Линейная скорость точки (см. рис. 1)

т.е

v=ωR

В векторном виде формулу для линейной скорости можно написать как векторное произведение: При этом модуль векторного произведения, по определению, равен ωRsin(ω, R), а направление совпадает с направлением поступательного движения правого винта его вращения от ω к R.

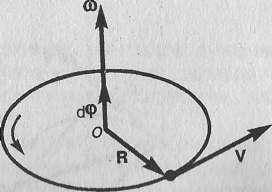
Если ω=const, то вращение равномерное и его можно характеризовать периодом вращения Т - временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2π. Так как промежутку времени Δt=Т соответствует Δφ=2π, то ω=2π/T, откуда

Т = 2π/ω.

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

n= 1/T = ω/(2π),

откуда

ω = 2πn.

Угловым ускорением называется векторная величина, равная первой производной yгловой скорости по времени:

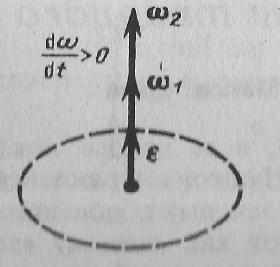
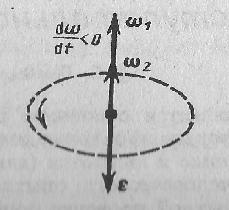
При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω (рис. 3), при замедленном - противонаправлен ему (рис. 4).

Тангенциальная составляющая ускорения aτ=dv/dt , v = ωR и Нормальная составляющая ускорения Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение аτ, нормальное ускорение аn) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами: s = Rφ, v = Rω, аτ = R?, an = ω2R. В случае равнопеременного движения точки по окружности (ω=const) ω = ω0 ± ?t, φ = ω0t ± ?t2/2, где ω0 — начальная угловая скорость.