6. Коллинеарные и компланарные векторы.

Два вектора называются коллинеарными, если они параллельны одной прямой (сонаправленными, если их направления совпадают; противоположнонаправленными, если их направления противоположны).

Три вектора называются компланарными, если они параллельны одной плоскости. Если смешанное произведение 3 векторов равно 0, то они компланарны. Если три вектора компланарны, то эта тройка не относится ни к правой, ни к левой.

7. Прямая на плоскости.

1)Ax+By+C=0 – общее уравнение прямой на плоскости. 2)- каноническое уравнение прямой, проходящей через точку M(x₀, y₀), параллельно направляющему вектору q(l,m).

3) => 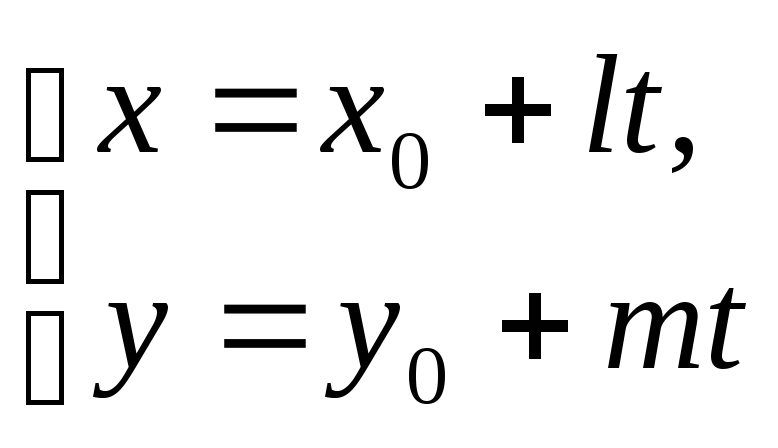- параметрическое уравнение прямой, проходящей через точку M(x₀, y₀), параллельно направляющему вектору q(l,m).

4)Если С не равно 0, то можно получить ур-е прямой в отрезках: - уравнение прямой в отрезках, где a и b – величины направленных отрезков, отсекаемых прямой от координатных осей.

5) Если B не равно 0, то можно получить ур-е с угловым коэффициентом. - уравнение прямой с угловым коэффициентом.

6) - уравнение прямой через 2 точки.

Взаимное располож прямых на п-ти:

Даны 2 прямые L₁: A₁x+B₁y+C₁z+D=0, L₂: A₂x+B₂y+C₂z+D=0. Следовательно, прямые: 1) совпадают, если ; 2) параллельны, если ; 3) пересекаются, если .

Прямые на пл-ти совп или парал если их напр векторы коллинеарны,а значит их корд пропорциональны

1)совпадают,если и

2)параллельны, если и

3)пересекаются,если

Если прямые L1 и L2 заданы Ур-м с угловым коэф L1:y=k1x+b1 и L2:y=k2x+b2 то эти прямые 1)совпад если k1=k2 u b1=b2 2)парал если k1=k2 u b1b2 3)пересек если k1k2

Угол между прямыми на:

Плоскость: заданы 2 прямые

Тогда

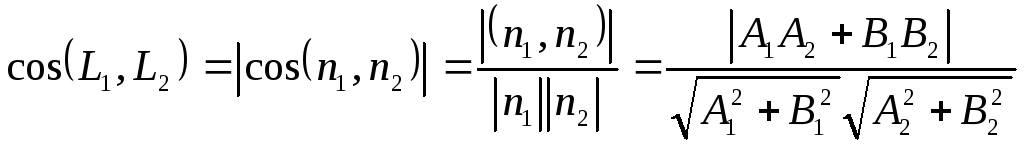
Если прямые заданы каноническим ур-м

Расстоние от точки до прямой на плоскосит:

8. Плоскость в пространстве.

1) Ax+By+Cz+D=0 – общее уравнение плоскости.

2) Если D не равно 0, то можно вывести уравнение плоскости в отрезках: , где , где а, b, c – величины направленных отрезков, отсекаемых плоскостью от координатных осей.

3) Уравнение плоскости по 3 точкам: Пусть . Если A, B, C не лежат на одной прямой, то уравнение можно найти по формул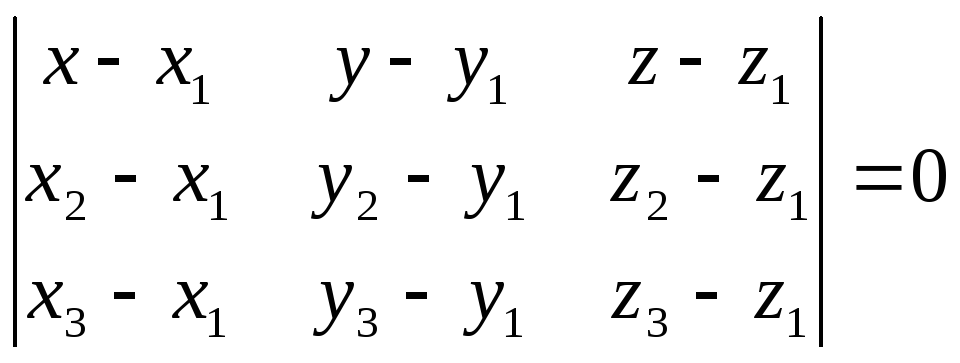е , где - координаты данных точек, а - координаты точки, принадлежащей плоскости P.

4)Ур-е через задан точку парал двум векторам А(x0,y0,z0), a(a1,a2,a3) u b(b1,b2,b3)

5)параметрическое ур-е

векторам А(x0,y0,z0), a(a1,a2,a3) u b(b1,b2,b3)

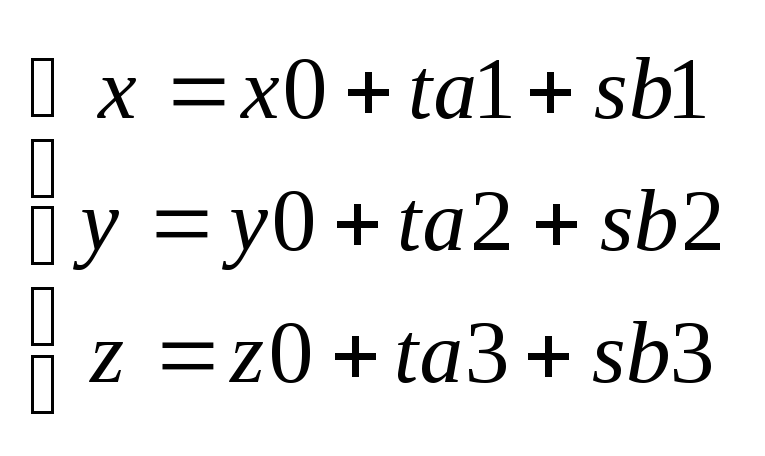
6)в векторном виде(получаем из параметрического)

r=r0+ta+sb

Взаимное расположение плоскостей

где - нормальные векторы плоскостей. Следовательно, плоскости: 1) совпадают, если 2) параллельны, если 3) в остальных случаях пересекаются.

Угол между плоскостями:

где - нормальные векторы плоскостей.

Расстояние от точки до плоскости

и точка M(x0, y0, z0).

9. Прямая в пространстве.

1) общее уравнение прямой – линия пересечения двух непараллельных плоскостей:

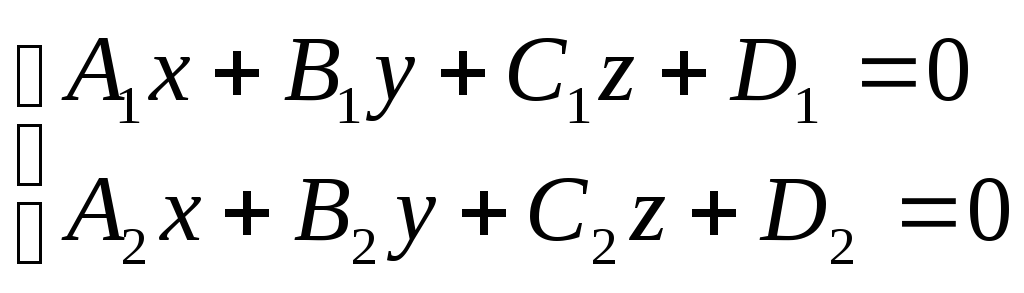
2) -каноническое уравнение прямой, проходящей через точку M(x₀, y₀, z₀) параллельно направляющему вектору q(l, m, n).

3)

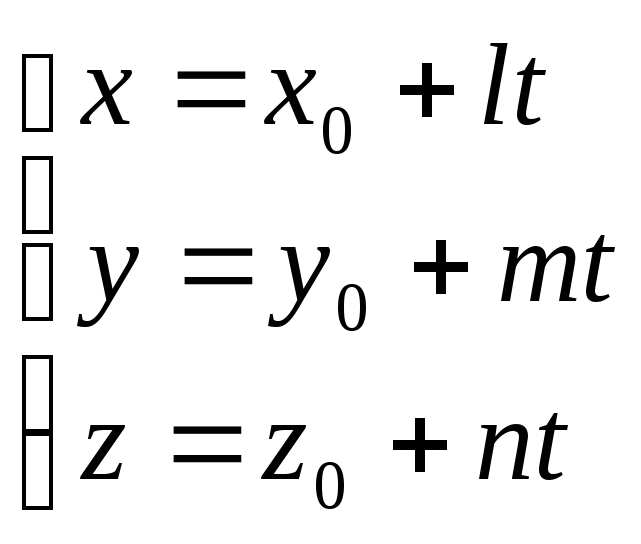- параметрическое уравнение прямой.

Взаимное располож.прямых в пространстве:

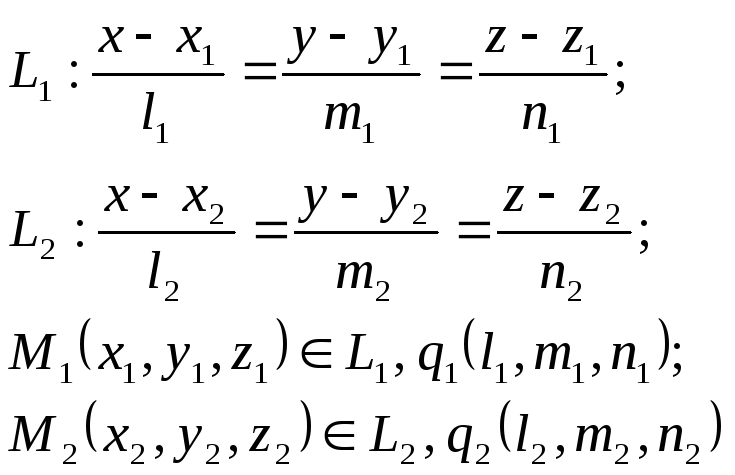
Тогда прямые L₁ и L₂:

1) скрещиваются, если

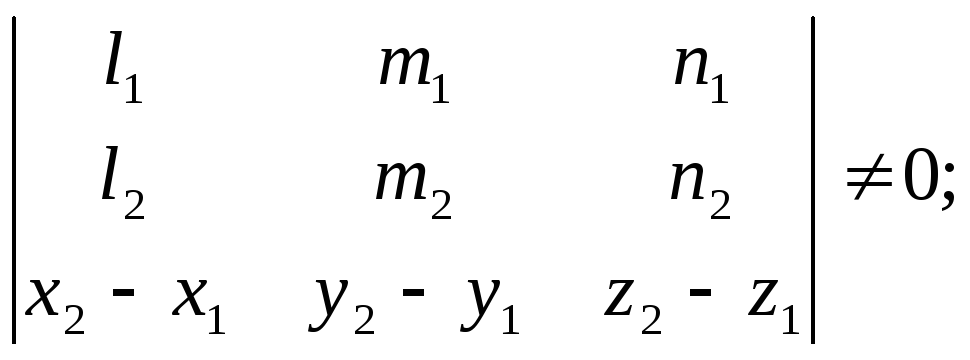
2) пересекаются, если 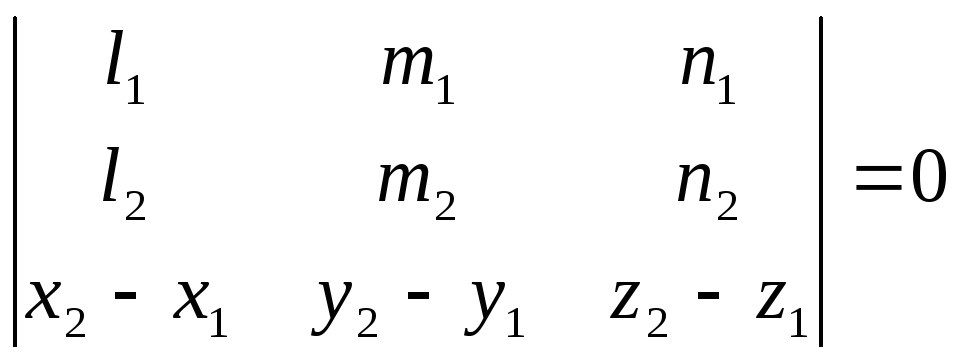и вектор q₁ не коллинеарен вектору q₂.

3) параллельны, если и точка

4) совпадают, если и точка

Угол между прямыми в пространстве:

Пусть заданы прямые 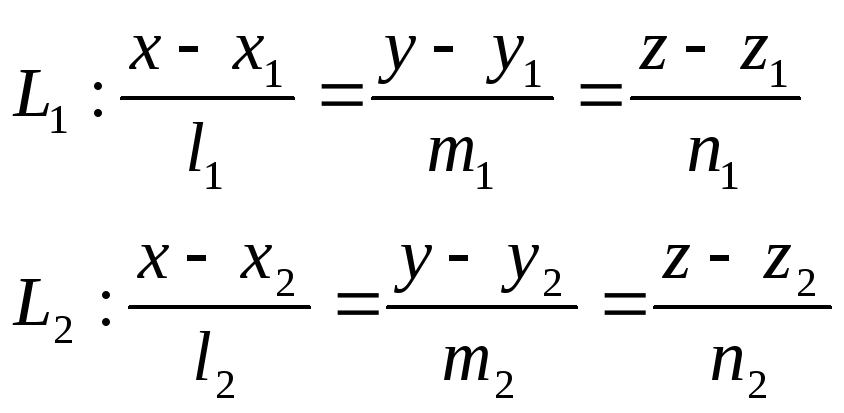где и - направляющие векторы прямых. Тогда Расстояние от точки до прямой в пространстве:

Прямая и точка M(x₀, y₀, z₀). Тогда расстояние от точки M до прямой L:, где M₀ – точка, принадлежащая прямой L, q – направляющий вектор прямой L.

Расстояние между скрещивающимися прямыми: Пусть заданы прямые 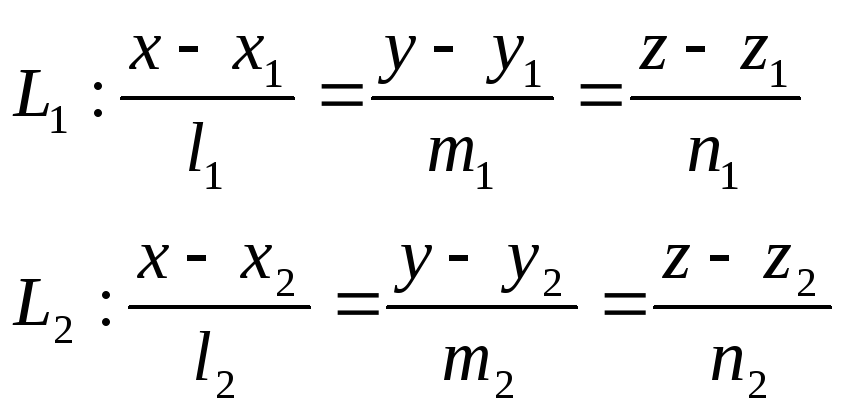где и - направляющие векторы прямых. Также Тогда расстояние между скрещивающимися прямыми:

Взаимное расположение прямой и плоскости в пространстве:

, задана прямая и точка , где - направляющий вектор прямой, - вектор нормали плоскости.

1) Прямая лежит в плоскости, тогда , т.е. ииточка .

2) Прямая параллельна плоскости, тогда , т.е. иточка .

3) Прямая пересекает плоскость, тогда , т.е.

Угол между прямой и плоскостью:

, задана прямая, где - направляющий вектор прямой, - вектор нормали плоскости.