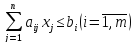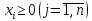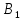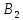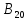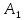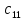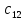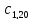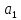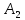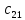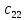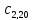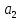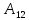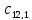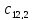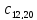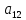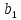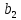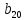Решение:
Для построения области допустимых решений строим в системе координат соответствующие данным ограничениям-неравенствам граничные прямые:
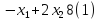
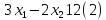
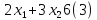
Строим вектор
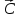 ,
координаты которого являются коэффициентами
целевой функции.
,
координаты которого являются коэффициентами
целевой функции.
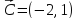
Перпендикулярно
к построенному вектору проводим линию
уровня
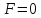
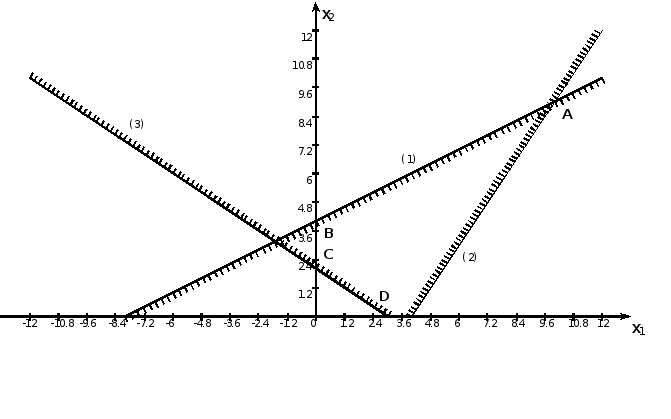
Областью допустимых
решений является фигура
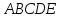 .
.
Перемещаем линию
уровня
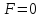 в антиградиентном направлении вектора
так, чтобы она касалась области допустимых
решений в крайней точке. Решением на
минимум является точка
в антиградиентном направлении вектора
так, чтобы она касалась области допустимых
решений в крайней точке. Решением на
минимум является точка
 ,
координаты которой находим как точку
пересечения прямых (1) и (2).
,
координаты которой находим как точку
пересечения прямых (1) и (2).
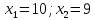
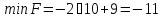
7.
В цехе имеется 12 станков, на которых необходимо обработать 20 деталей. Известна стоимость обработки каждой из деталей на каждом из станков. Общая стоимость обработки всех деталей должна быть минимальна. К какому классу можно отнести данную задачу? Как ее решать?
Решение:
Данная задача относится к классу транспортных задач.
|
Станки |
Детали |
Количество деталей, которые сможет обработать станок |
||||
|
|
|
|
|
|
||
|
Затраты на обработку одной детали |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Количество обрабатываемых деталей |
|
|
|
|
|
|
Матрица:

где
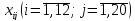 обозначает количество деталей
обозначает количество деталей
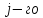 вида, обрабатываемых на
вида, обрабатываемых на
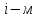 станке.
станке.
Данная задача решается методом потенциалов.
8.
На предприятии необходимо наладить систему снабжения производства сырьем и своевременный запуск партии товаров в производство. Какие задачи при этом необходимо решать? К какому классу их можно отнести. Опишите аналитически в общем виде данную задачу.
Решение:
Это задача линейного программирования.
Опишем аналитически в общем виде данную задачу:
Пусть некоторая
производственная единица (цех, завод,
объединение и т.д.), исходя из конъюктуры
рынка, технических или технологических
возможностей и имеющихся ресурсов,
может выпускать
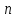 различных видов продукции (товаров),
известных под номерами, обозначаемыми
индексами
различных видов продукции (товаров),
известных под номерами, обозначаемыми
индексами
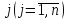 .
Ее будем обозначать
.
Ее будем обозначать
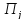 .
Предприятие при производстве этих видов
продукции должно ограничиваться
имеющимися видами ресурсов, технологий,
других производственных факторов
(сырья, полуфабрикатов, рабочей силы,
оборудования, электроэнергии и т.д.).
Все эти виды ограничивающих факторов
называют ингредиентами
.
Предприятие при производстве этих видов
продукции должно ограничиваться
имеющимися видами ресурсов, технологий,
других производственных факторов
(сырья, полуфабрикатов, рабочей силы,
оборудования, электроэнергии и т.д.).
Все эти виды ограничивающих факторов
называют ингредиентами
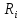 .Пусть
их число равно
.Пусть
их число равно
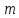 .
припишем им индекс
.
припишем им индекс
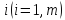 .
Они ограничены, и их количества равны
соответственно
.
Они ограничены, и их количества равны
соответственно
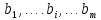 условных единиц. Таким образом
условных единиц. Таким образом
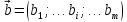 – вектор ресурсов. Известна экономическая
выгода (мера полезности) производства
продукции каждого вида, исчисляемая,
скажем, по отпускной цене товара, его
прибыльности, издержкам производства,
степени удовлетворения потребностей
и т.д. Пример в качестве такой меры,
например, цену реализации
– вектор ресурсов. Известна экономическая
выгода (мера полезности) производства
продукции каждого вида, исчисляемая,
скажем, по отпускной цене товара, его
прибыльности, издержкам производства,
степени удовлетворения потребностей
и т.д. Пример в качестве такой меры,
например, цену реализации
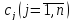 ,
то есть
,
то есть
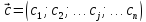 –вектор цен. Известны также технологические
коэффициенты
–вектор цен. Известны также технологические
коэффициенты
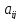 ,
которые указывают, сколько единиц
,
которые указывают, сколько единиц
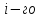 ресурса требуется для производства
продукции
ресурса требуется для производства
продукции
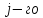 вида. Матрицу коэффициентов
вида. Матрицу коэффициентов
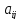 называют технологической и обозначают
буквой
называют технологической и обозначают
буквой
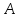 .
Имеем
.
Имеем
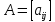 .
Обозначим через
.
Обозначим через
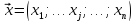 план производства, показывающий, какие
виды товаров
план производства, показывающий, какие
виды товаров
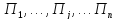 нужно производить и в каких количествах,
чтобы обеспечить предприятию максимум
объема реализации при имеющихся ресурсах.
нужно производить и в каких количествах,
чтобы обеспечить предприятию максимум
объема реализации при имеющихся ресурсах.
Так как
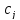 – цена реализации единицы
– цена реализации единицы
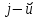 продукции, цена реализованных
продукции, цена реализованных
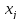 единиц будет равна
единиц будет равна
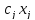 ,
а общий объем реализации
,
а общий объем реализации
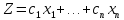
Это выражение – целевая функция, которую нужно максимизировать.
Так как
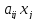 – расход
– расход
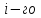 ресурса на производства
ресурса на производства
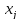 единиц
единиц
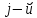 продукции, то, просуммировав расход
продукции, то, просуммировав расход
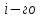 ресурса на выпуск всех
ресурса на выпуск всех
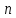 видов продукции, получим общий расход
этого ресурса, который не должен
превосходить
видов продукции, получим общий расход
этого ресурса, который не должен
превосходить
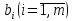 единиц:
единиц:
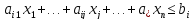
Чтобы искомый план
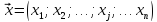 был реален, наряду с ограничениями на
ресурсы нужно наложить условие
неотрицательности на объемы
был реален, наряду с ограничениями на
ресурсы нужно наложить условие
неотрицательности на объемы
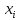 выпуска продукции:
выпуска продукции:
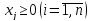
Таким образом, модель задачи примет вид.
Найти:
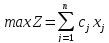
при ограничениях: