
1.
Если в исходной задаче есть неограниченные по знаку искомые переменные, то оказывает ли это какое-либо влияние на двойственную ей задачу?
Решение:
Да, оказывает влияние.
Двойственная задача со смешанными ограничениями составляется с соблюдением следующих дополнительных правил.
1. Если на переменную
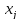 прямой задачи наложено условие
неотрицательности, то
прямой задачи наложено условие
неотрицательности, то
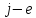 условие системы ограничений двойственной
задачи записывается в виде неравенства
и наоборот.
условие системы ограничений двойственной
задачи записывается в виде неравенства
и наоборот.
2. Если на переменную
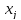 прямой задачи не наложено условие
неотрицательности, то
прямой задачи не наложено условие
неотрицательности, то
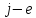 ограничение двойственной задачи
записывается в виде строгого равенства.
ограничение двойственной задачи
записывается в виде строгого равенства.
3. Если в прямой задаче имеются ограничения равенства, то на соответствующие переменные двойственной задачи не налагается условие неотрицательности.
2.
Крупный международный концерн собирается инвестировать средства в свои филиалы. Задача может быть решена в течение ограниченного промежутка времени и средств. Можно ли рассматривать ее как задачу динамического программирования? Приведите постановку задачи. Опишите алгоритм решения задачи динамического программирования.
Решение:
Эту задачу можно рассматривать как задачу динамического программирования.
Постановка задачи:
Пусть на инвестирование
в филиалы выделяется некоторый объем
материальных ресурсов
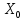 .
Имеется
.
Имеется
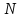 филиалов, между которыми необходимо
распределить данный ресурс. Обозначим
через
филиалов, между которыми необходимо
распределить данный ресурс. Обозначим
через
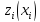 прибыль, которую приносит концерну
выделение
прибыль, которую приносит концерну
выделение
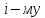 филиалу
филиалу
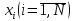 единиц ресурса. Предполагается, что
размер прибыли зависит как от выделенного
количества ресурса, так и от филиала.
Причем констатируется, что: прибыль,
получаемая каждым предприятием,
измеряется в одних и тех же единицах,
прибыль, получаемая любым из филиалов,
не зависит от того, какое количество
этого ресурса выделено другим филиалам.
Общая прибыль концерна состоит из
прибылей отдельного филиала.
единиц ресурса. Предполагается, что
размер прибыли зависит как от выделенного
количества ресурса, так и от филиала.
Причем констатируется, что: прибыль,
получаемая каждым предприятием,
измеряется в одних и тех же единицах,
прибыль, получаемая любым из филиалов,
не зависит от того, какое количество
этого ресурса выделено другим филиалам.
Общая прибыль концерна состоит из
прибылей отдельного филиала.
Чтобы решать
задачу, применим аппарат функциональных
уравнений Р. Беллмана. Погружаем ее в
семейство подобных задач распределения.
Вместо решения одной задачи с заданными
объемом ресурса
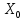 и фиксированным числом предприятий
и фиксированным числом предприятий
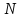 рассмотрим их семейства, в которых
объем выделенного ресурса
рассмотрим их семейства, в которых
объем выделенного ресурса
 может меняться от нуля до
может меняться от нуля до
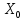 и число предприятий от 1 до N.
Статистическая задача распределения
при таком подходе приобретет динамический
характер. Введем последовательность
функций
и число предприятий от 1 до N.
Статистическая задача распределения
при таком подходе приобретет динамический
характер. Введем последовательность
функций
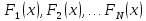 ,
где
,
где
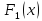 – это максимальная прибыль, если бы
ресурс
– это максимальная прибыль, если бы
ресурс
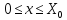 был выделен только одному филиалу,
был выделен только одному филиалу,
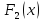 – максимальная прибыль, полученная при
условии, что ресурс
– максимальная прибыль, полученная при
условии, что ресурс
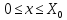 был распределен двум предприятиям и
т.д. Пусть наконец
был распределен двум предприятиям и
т.д. Пусть наконец
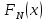 – максимальная прибыль, получаемая от
распределения ресурса
– максимальная прибыль, получаемая от
распределения ресурса
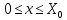 между
между
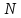 предприятиями. Очевидно, что
предприятиями. Очевидно, что
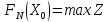
В двух случаях
элементы последовательности
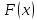 имеют особенно простой вид:
имеют особенно простой вид:
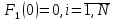
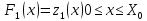
Пусть ресурс
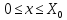 распределяется между двумя предприятиями.
Если
распределяется между двумя предприятиями.
Если
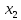 – объем ресурса, выделенного второму
предприятию, то его прибыль составит
– объем ресурса, выделенного второму
предприятию, то его прибыль составит
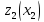 .
Оставшийся ресурс
.
Оставшийся ресурс
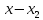 распределяется наилучшим образом. Общая
прибыль для двух предприятий составит:
распределяется наилучшим образом. Общая
прибыль для двух предприятий составит:
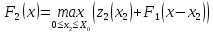
Аналогично
рассуждая, найдем рекуррентное
соотношение, связывающее
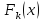 и
и
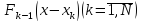 для произвольных значений
для произвольных значений
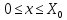 .
В самом деле, пусть
.
В самом деле, пусть
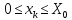 – количество ресурса, выделяемое для
-го предприятия. Тогда, каково бы ни было
значение
– количество ресурса, выделяемое для
-го предприятия. Тогда, каково бы ни было
значение
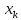 ,
согласно принципу оптимальности,
оставшийся ресурс
,
согласно принципу оптимальности,
оставшийся ресурс
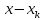 распределится между остальными
распределится между остальными
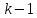 предприятиями наилучшим образом. Так
как
предприятиями наилучшим образом. Так
как
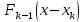 известно,
то
известно,
то
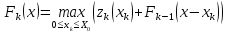
Решение исходной
задачи получим при
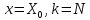 ,
т.е. из рекуррентного соотношения:
,
т.е. из рекуррентного соотношения:
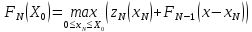
Найдя
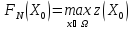
определяем
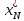 .
Зная
.
Зная
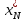 находим
находим
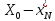 ,
следовательно:
,
следовательно:
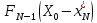
Из выражения:
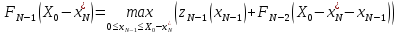
находим
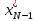 и т.д., т.е. процесс разворачивается в
обратном направлении, при котором
находятся уже не условно-оптимальные,
а оптимальные значения функции цели на
каждом этапе и оптимальное выделение
ресурса для одного, двух и более
предприятий.
и т.д., т.е. процесс разворачивается в
обратном направлении, при котором
находятся уже не условно-оптимальные,
а оптимальные значения функции цели на
каждом этапе и оптимальное выделение
ресурса для одного, двух и более
предприятий.
3.
Что необходимо предпринять, если при поиске по симплексу оптимума некоторой функции происходит циклическое движение?
