Найдите значение выражения

.

.

.

.

.

.

.

.

+

+

-

+.

+.

.

.

-.

--

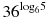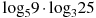
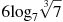
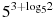
, если .

Найдите , если .

Найдите , если .

Тема 1.3. Основы тригонометрии

Формулы перехода от градусного измерения к радианному, и от радианного к градусному.

Дайте определения тригонометрических функций числового аргумента и укажите их области определения.

Как определяются знаки тригонометрических функций по четвертям?

Какие тригонометрические функции являются четными, и какие нечетными?

Числовые значения тригонометрических функций от 0 до π/2.

Основные тригонометрические тождества.

Выразите тригонометрические функции через синус, косинус, тангенс и котангенс соответственно.

Дайте определение периодической функции.

Какие числа являются периодами функций синуса и косинуса, тангенса и котангенса.

Какие формулы называются формулами приведения?

Сформулируйте правила названий тригонометрических функций при составлении формул приведения.

Сформулируйте правило знаков при составлении формул приведения.

Формулы тригонометрических функций удвоенного аргумента.

Запишите в общем виде решение уравнений sinx=a. Приведите примеры частных случаев.

Запишите в общем виде решение уравнений cosx=a. Приведите примеры частных случаев.

Запишите в общем виде решение уравнений tgx=a. Приведите примеры.

Запишите в общем виде решение уравнений ctgx=a. Приведите примеры.

Какие тригонометрические уравнения называются простейшими?

Перечислите основные способы решения тригонометрических уравнений.

Запишите в общем виде решение неравенств sinx>a и sinx<a. Приведите примеры.

Запишите в общем виде решение уравнений cosx>a и cosx<a. Приведите примеры.

Запишите в общем виде решение уравнений tgx>a и tgx<a. Приведите примеры.

Запишите в общем виде решение уравнений ctgx>a и ctgx<a. Приведите примеры.

Практические задания по теме «Основы тригонометрии»

Найдите значение выражения:

Найдите значения других трёх основных тригонометрических функций, если:

Упростите выражение:

Решите уравнение:

Постройте график функции:

Найдите значение выражения:

Решите неравенство:

Тема1.4. Функции, их свойства и графики

Что такое функция?

Что называется областью определения функции?

Что такое график функции?

Какие способы задания функции вы знаете? Приведите примеры различных способов задания функции.

Какая функция называется обратимой?

Какие функции называют взаимно обратными?

Сформулируйте определения четной и нечетной функции.

Приведите примеры таких функций.

Какие функции называются периодическими? Приведите примеры периодических и непериодических функций.

Как расположены графики взаимно обратных функций?

Какие геометрические особенности имеют области определения четных и нечетных функций

Какие геометрические особенности имеют графики четных, нечетных и периодических функций?

Какая функция называется возрастающей? Когда она называется строго возрастающей? Приведите примеры таких функций.

Какая функция называется убывающей? Когда она называется строго убывающей? Приведите примеры таких функций.

Какие функции называются монотонными? Приведите примеры монотонных функций.