6. Исследование зависимостей

6.1. Постановка задачи

Пусть ГС представляет собой многомерную с.в. , где результирующий признак (выходная переменная),выходные (объясняющие) переменные, факторы, влияющие на .Тогда возникает задача исследования связей по ограниченному объему наблюдений за : мы должны по ограниченному объему наблюдений составить суждение о наличии связей между переменными . Как правило, такие связи не функциональные, а стохастической природы (линейные или нелинейные, тесные или слабые). Эти связи выявляются (оцениваются) на основе наблюдений, т.е. по выборке.

Возникают следующие основные группы задач:

1) Существует ли связь между рассматриваемыми переменными?

2) Если связь существует, то каков вид связи? (какова структура зависимости между переменными?)

Итак пусть результирующие (выходные) переменные и (входные) переменные.

Пусть любая из выходных переменных.

Тогда: ,где "шум" эксперимента, т.е. находится по с точностью до (в качестве рассматриваются и ). Уточним поставленные выше задачи:

1) Существует ли связь между и и какова теснота этой связи?

2) Если связь значимая (достоверная), то необходимо оценить ,т.е. найти вид (структуру) связи между и набором

3) Пусть модель достоверная ( связь значимая, тесная), тогда возникает необходимость упрощения модели при сохранении достоверности, т.е. нельзя ли исключить из модели несущественные переменные . Для этого разработаны статистические процедуры, одна из них состоит в оценке значимости коэффициента ,стоящего в . При коэффициент не значим, чем больше , тем больше "вклад" в модель фактора Для оценки "вклада" используется критерий Стьюдента.

Если не значим, то из модели можно исключить слагаемое .

4) Выявление "очищенных" связей.

Рассматривается задача непосредственного (без учета взаимного влияния факторов) влияние входной переменной на .

Связь может быть линейной или нелинейной. Для оценки тесноты связи существует мера связи. Исследование связи между двумя переменными необходимо начинать с выявления линейной связи, что делается с использованием парного коэффициента корреляции. Если по найденному коэффициенту корреляции отвечаем на вопрос о наличии значимой (тесной) связи, то рассматривается задача о нахождении структуры связи

,где

Необходимо найти "хорошие" оценки и . Если на влияет несколько входных переменных, то рассматривают вопрос о наличии множественной связи. Мерой множественной связи является коэффициент множественной корреляции. Если этот коэффициент значим (что проверяется с помощью соответствующей процедуры) , то говорят , что имеет место тесная (достоверная) связь, и можно решать вопрос о виде (структуре) связи . В линейном случае имеем , т.е. оцениваются и тогда .

6.2. Линейная зависимость

Задачу о наличии линейной зависимости будем решать с точки зрения двух подзадач;

а) ответ на вопрос: имеется ли такая связь, какова ее теснота ?

б) построение вида связи, т.е. построение линейной модели (регрессии).

Для нахождения тесноты связи рассматривают парный коэффициент корреляции: 1) он является мерой лишь линейной связи;2) даже большое значение коэффициента не свидетельствует еще о наличии формульной зависимости, т.е. не указывает на причину и следствие.

Определим парный коэффициент корреляции как

где имеем наблюдение двумерная выборка,

Основные свойства :

1);

2) Если и независимы.

Если и независимы, в этом случае говорят, что и некоррелированы.

3) линейная связь (т.е. ), причем .

Пример 1. Влияние отравляющего воздействия брома на цветы гвоздики.

бром в мг/см; число цветков (в среднем)

X	Y	X	Y
3 4 6 7 8	3,2 2,9 3,7 2,2 1,8	10 12 15 16	2,3 1,7 0,8 0,3

Диаграмма рассеивания (корреляционное поле)

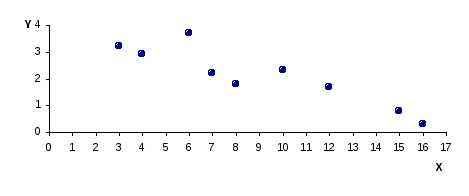
Корреляционное поле позволяет выдвинуть гипотезу о линейной связи между .и .

Эту задачу необходимо решать по двум направлениям:

1) найти тесноту связи;

2) если связь тесная (достоверная), то найти вид этой линейной связи.

Вычислим парный коэффициент корреляции

,

У нас: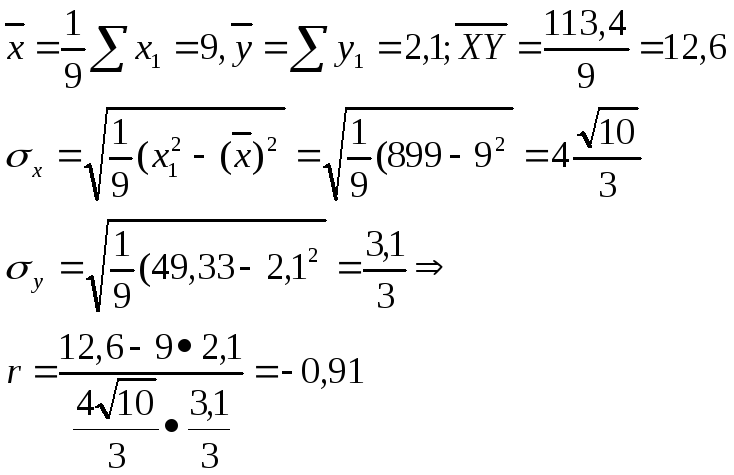

Т.к. , то это свидетельствует ,по-видимому, о наличии достоверной связи.

Возникает вопрос: что считать критерием достоверной связи? Выдвигаем гипотезу : связь отсутствует, т.е. теоретический коэффициент корреляции . Тогда, если отвергается, то связь следует считать достоверной. Для проверки гипотезы строится статистика

Оказывается статистика имеет распределение Стьюдента с степенями свободы (параметр распределения). Если , то связь следует считать достоверной, где находится по таблице

	4	5	6
	3,2	2,8	2,6	2,4	2,3	2,2	2,1	2,0	1,96

Заметим, что, поскольку связь достоверная при , то естественно найти такое , что связь достоверная при

Мы имеем связь между и , найдем ее.

Коэффициент корреляции значим, если или

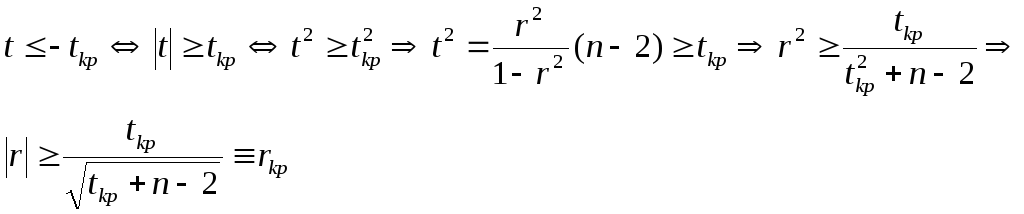
Вернемся к нашему примеру:

(по таблице)=2,3 и тогда

Связь достоверная!

Теперь, когда мы выяснили, что между и существует тесная связь, решается вторая задача-нахождение вида линейной связи. Для этого необходимо оценить коэффициенты линейной модели: и любые. Из всего класса линейных моделей необходимо найти "лучшую" модель - наилучшую линию подгонки. Модель та лучше, для которой разброс наблюдений вокруг этой модели меньший. В качестве меры пригодности возьмем.

Здесь отклонение результатов ого наблюдения от прямой . Имеем:

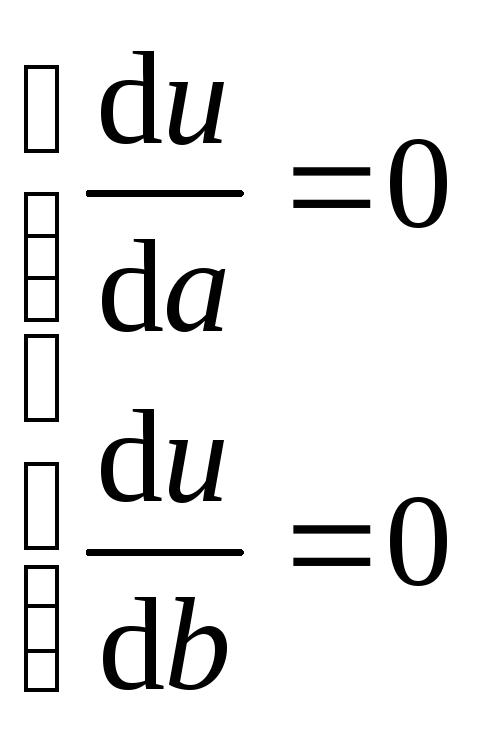- необходимое условие экстремума.

Решение этой системы и и даст -линию наилучшей подгонки. Получаем формулы для оценки и

Вернемся к примеру. Определим наилучшую линию подгонки,

исходя из данных формул. Имеем: .Тогда и, следовательно, линия наилучшей подгонки будет иметь вид:

-лучшая из класса линейных моделей. Заметим, что

Построенная таким образом модель может быть использована для решения задач прогнозирования, при этом надо иметь в виду следующее:

1. для задач интерполяции( нахождение внутри интервала наблюдений);

2) с большой долей осторожности нужно исследовать модель вне окна наблюдений(экстраполяции).

При (число цветков отрицательно!) .

Рассмотренный аппарат может быть использован для построения линейных моделей. Существует много зависимостей, которые путем замены переменных сводятся к линейным относительно новых переменных, что позволяет использовать приведенный аппарат для оценки параметров новой линейной зависимости, а следовательно и для параметров исходной модели.

Пример 2. Примеры моделей, сводящихся к линейным.

N	Зависимость	Преобразование	Параметры
1.	Y=
2.
3.
4.	задано