
- •Основы статистического анализа
- •1 Основные задачи статистического анализа
- •1.1 Выборочный метод
- •1.2 Основные задачи статистического анализа
- •Задача 1
- •Пример 1
- •2 Первичная статистическая обработка результатов наблюдений
- •2.1 Графическое представление данных
- •2.2 Числовые характеристики вариационного ряда
- •2.3 Интервальные оценки (доверительные интервалы)
- •2.4 Определение достаточного объема выборки
- •3 Сравнение двух выборок.
- •4. Статистическая оценка расхождения между выборочными частотами.
- •5. Сравнение долей
- •6. Исследование зависимостей
- •6.1. Постановка задачи
- •6.2. Линейная зависимость
- •6.4. Множественная линейная зависимость
2.2 Числовые характеристики вариационного ряда
Пусть
наблюдается с.в.
![]() :
:
![]() -
результаты наблюдений (выборка). Признак
-
результаты наблюдений (выборка). Признак
![]() характеризуется своими числовыми
характеристиками:
характеризуется своими числовыми
характеристиками:
![]() .
Обозначим
.
Обозначим
![]() -
произвольный неизвестный параметр.
Одна из важнейших задач, которую мы
сформулировали выше, следующая: как по
результатам наблюдений оценить
неизвестный параметр
-
произвольный неизвестный параметр.
Одна из важнейших задач, которую мы
сформулировали выше, следующая: как по
результатам наблюдений оценить
неизвестный параметр
![]() .
.
Обозначим
![]() - произвольную оценку параметра
- произвольную оценку параметра
![]() .
Естественный вопрос: какие требования
следует предъявить к оценкам и какую
оценку следует выбрать из множества
всех оценок. Коль скоро мы определили,
что такое оценка, то надо научиться
сравнивать разные оценки и научиться
отыскивать наилучшие оценки. Представляется
довольно очевидным, что поскольку в
разных опытах выборки
.
Естественный вопрос: какие требования
следует предъявить к оценкам и какую
оценку следует выбрать из множества
всех оценок. Коль скоро мы определили,
что такое оценка, то надо научиться
сравнивать разные оценки и научиться
отыскивать наилучшие оценки. Представляется
довольно очевидным, что поскольку в
разных опытах выборки
![]() ,
вообще говоря, различны, то сравнивать
надо не по их значениям для отдельных
выборок
,
вообще говоря, различны, то сравнивать
надо не по их значениям для отдельных
выборок
![]() ,
а по некоторым их суммарным характеристикам.
Очевидно, любая оценка
,
а по некоторым их суммарным характеристикам.
Очевидно, любая оценка
![]() как функция от наблюдений
как функция от наблюдений
![]() является с.в. Рассмотрим две оценки:
является с.в. Рассмотрим две оценки:

![]()




























![]()
![]()
Какая
оценка лучше? Очевидно та, которая в
среднем ближе к
![]() .
Таким образом, из всех оценок нужно
выбирать те, которые в среднем совпадают
с оцениваемым параметром
.
Таким образом, из всех оценок нужно
выбирать те, которые в среднем совпадают
с оцениваемым параметром
![]() .
Итак, имеем первое требование к оценкам
- несмещенность,
т.е.
.
Итак, имеем первое требование к оценкам
- несмещенность,
т.е.
![]() .
.
К акие
еще требования необходимо предъявить
к оценкам, чтобы еще более сузить класс
оценок.
акие
еще требования необходимо предъявить
к оценкам, чтобы еще более сузить класс
оценок.
Снова обратимся к рисунку:












![]()













![]()
![]()
Ясно,
что вторая оценка предпочтительнее,
т.к. она имеет меньший разброс значений
вокруг
![]() ,
а, следовательно, является более точной.
Как мы помним, мерой разброса является
дисперсия; чем меньше дисперсия, тем
точнее в среднем оценка. Поэтому
естественно из множества несмещенных
оценок выбрать оценку с минимальной
дисперсией, т.е. такую оценку
,
а, следовательно, является более точной.
Как мы помним, мерой разброса является
дисперсия; чем меньше дисперсия, тем
точнее в среднем оценка. Поэтому
естественно из множества несмещенных
оценок выбрать оценку с минимальной
дисперсией, т.е. такую оценку
![]() ,
что
,
что
![]() где
где
![]() -
несмещенная оценка.
-
несмещенная оценка.
 Такую
оценку будем называть эффективной.
Итак, имеем:
Такую
оценку будем называть эффективной.
Итак, имеем:
Наконец,
нетрудно увидеть еще одно естественное
требование к оценкам: Если
![]() ,
то
,
то
![]() (должна!). Такую оценку будем называть
состоятельной.
(должна!). Такую оценку будем называть
состоятельной.
И так:
так:
Итак,
найти «хорошую» оценку для неизвестного
параметра
![]() - это найти несмещенную, эффективную и
состоятельную оценку. Как ее найти?
Существуют различные методы нахождения,
например, метод максимального
правдоподобия.
- это найти несмещенную, эффективную и
состоятельную оценку. Как ее найти?
Существуют различные методы нахождения,
например, метод максимального
правдоподобия.
Пример3. Приведем «хорошие» оценки для основных числовых характеристик ГС:
-
 -
среднее арифметическое;
-
среднее арифметическое; -
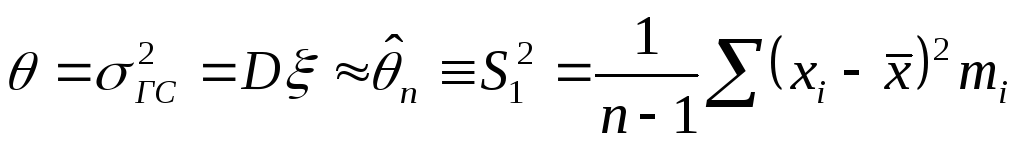 -
выборочная дисперсия;
-
выборочная дисперсия; -
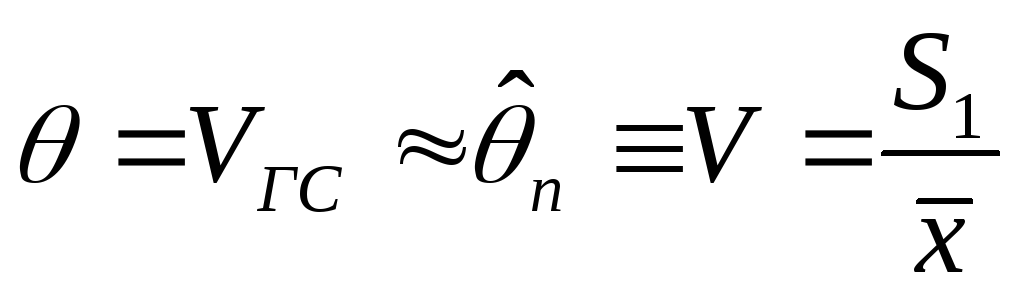 -
выборочная вариация;
-
выборочная вариация; -
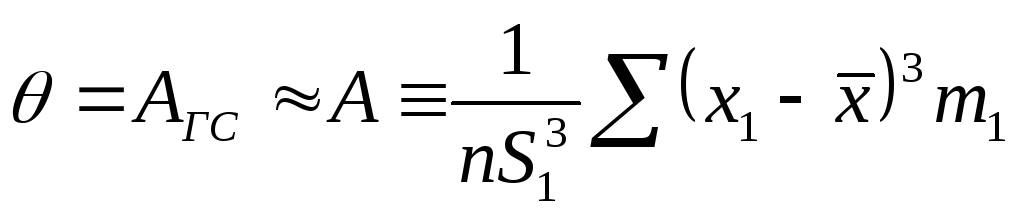 -
выборочный коэффициент асимметрии;
-
выборочный коэффициент асимметрии; -
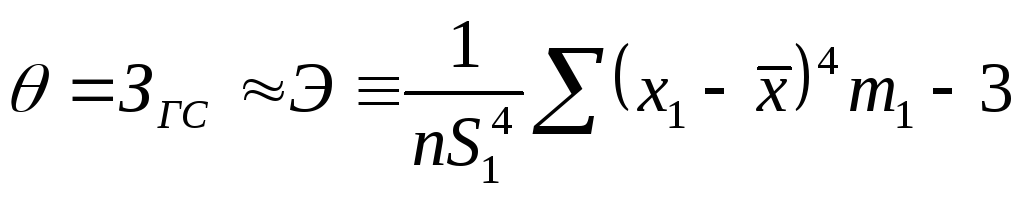 -
выборочный коэффициент эксцесса;
-
выборочный коэффициент эксцесса;
Замечание
1. Для простоты
вычислений в случае равностоящих
![]() (
(![]() )
удобно вводить в рассмотрение «ложный»
нуль (центр), который расположен
приблизительно в середине ряда наблюдений.
Тогда вместо исходного вариационного
ряда рассматривают вспомогательный,
который получается заменой переменных
)
удобно вводить в рассмотрение «ложный»
нуль (центр), который расположен
приблизительно в середине ряда наблюдений.
Тогда вместо исходного вариационного
ряда рассматривают вспомогательный,
который получается заменой переменных
![]() ,
где
,
где
![]() -
«ложный» нуль,
-
«ложный» нуль,
![]() -
расстояние между соседними вершинами
ряда наблюдений.
-
расстояние между соседними вершинами
ряда наблюдений.
Тогда:
![]() ,
,
![]()
и, следовательно,
![]() .
.
Пример 4. Выборка 250, 260, 250, 270, 260, 280, 280, 300, 300, 290, 290, 300, 250, 270, 280.
Вариационный ряд:
![]() ;
;
|
|
250 |
260 |
270 |
280 |
290 |
300 |
|
|
4 |
2 |
2 |
3 |
2 |
3 |
Используем
преобразование исходного ряда:
![]() ,
где
,
где
![]() ,
,
![]() .
Тогда будем иметь новый вариационный
ряд:
.
Тогда будем иметь новый вариационный
ряд:
|
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
|
|
4 |
2 |
2 |
3 |
2 |
3 |
Следовательно,
![]() .
И тогда
.
И тогда
![]() ,
,
![]() ,
.
,
.
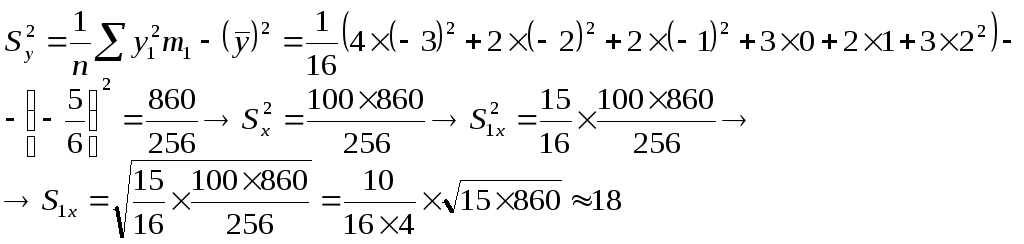 .
.
Очевидно,
прямой подсчет данных характеристик
без рассмотрения вспомогательного
вариационного ряда
![]() вызвал бы значительно больше затраты
вычислительного плана.
вызвал бы значительно больше затраты
вычислительного плана.
