
- •Основы статистического анализа
- •1 Основные задачи статистического анализа
- •1.1 Выборочный метод
- •1.2 Основные задачи статистического анализа
- •Задача 1
- •Пример 1
- •2 Первичная статистическая обработка результатов наблюдений
- •2.1 Графическое представление данных
- •2.2 Числовые характеристики вариационного ряда
- •2.3 Интервальные оценки (доверительные интервалы)
- •2.4 Определение достаточного объема выборки
- •3 Сравнение двух выборок.
- •4. Статистическая оценка расхождения между выборочными частотами.
- •5. Сравнение долей
- •6. Исследование зависимостей
- •6.1. Постановка задачи
- •6.2. Линейная зависимость
- •6.4. Множественная линейная зависимость
2 Первичная статистическая обработка результатов наблюдений
Пусть
имеется выборка![]() из
из
![]() .
Обработку результатов наблюдений
начинают с построения общей статистической
модели, которая включает в себя:
.
Обработку результатов наблюдений
начинают с построения общей статистической
модели, которая включает в себя:
-
графическое представление данных (полигон, гистограмма);
-
нахождение оценок для неизвестных параметров наблюдаемого признака
 .
.
Построение общей модели позволяет ответить на 2 вопроса:
а) решить в первом приближении поставленную задачу относительно ГС или изучаемого процесса;
б) нужна ли более точная модель.
Саму
обработку данных
![]() начинают с исключения ошибочных
(неоднородных) данных, для чего
используется «правило 3 6», используя
это правило, мы исключим из рассмотрения
неоднородные данные.
начинают с исключения ошибочных
(неоднородных) данных, для чего
используется «правило 3 6», используя
это правило, мы исключим из рассмотрения
неоднородные данные.
2.1 Графическое представление данных
Пусть
![]() - выборка из ГС, причем
- выборка из ГС, причем
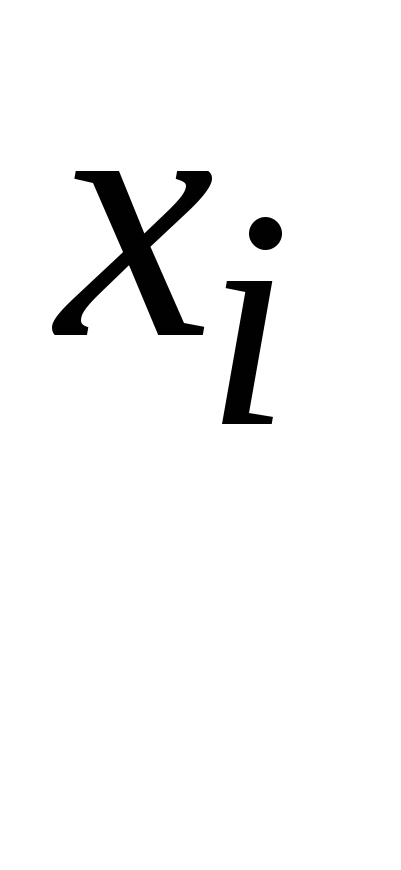 могут совпадать. Обозначим
могут совпадать. Обозначим
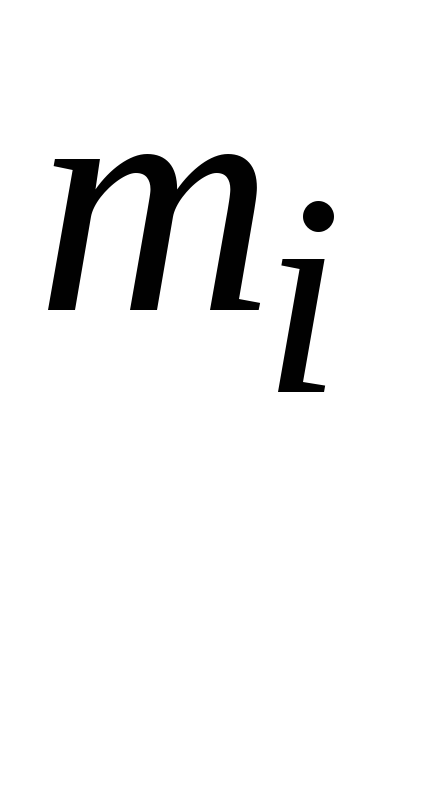 - число элементов выборки, равных
- число элементов выборки, равных
![]() .
Тогда
.
Тогда
![]() .
.
Расположим
выборку в порядке возрастания:
![]() - вариационный ряд. Удобно вариационный
ряд представлять в виде таблицы:
- вариационный ряд. Удобно вариационный
ряд представлять в виде таблицы:
-

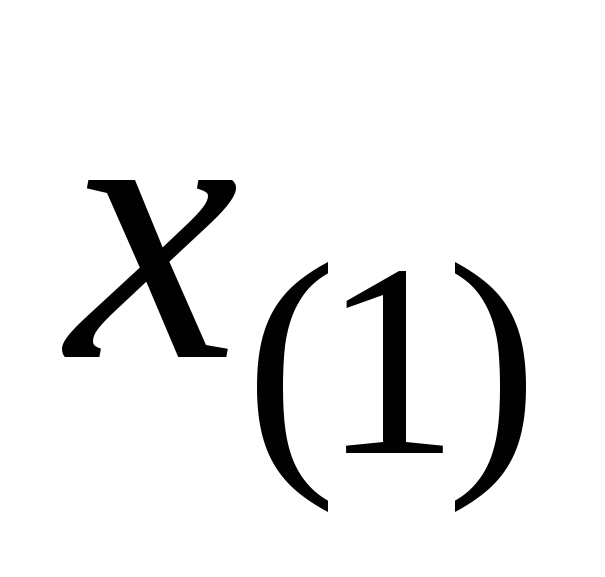

. . .
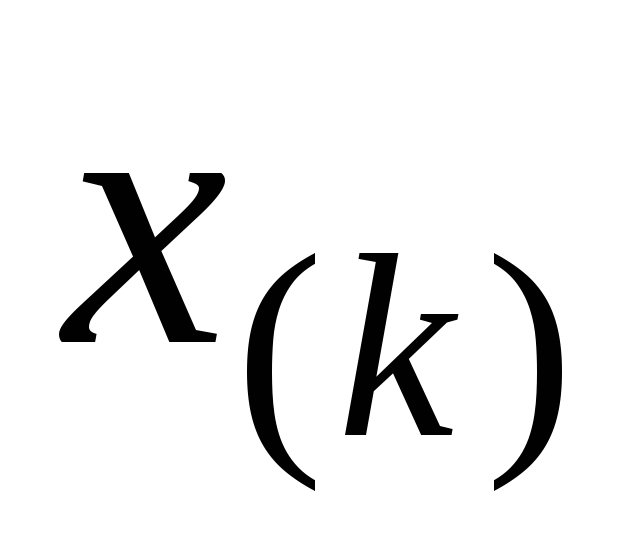
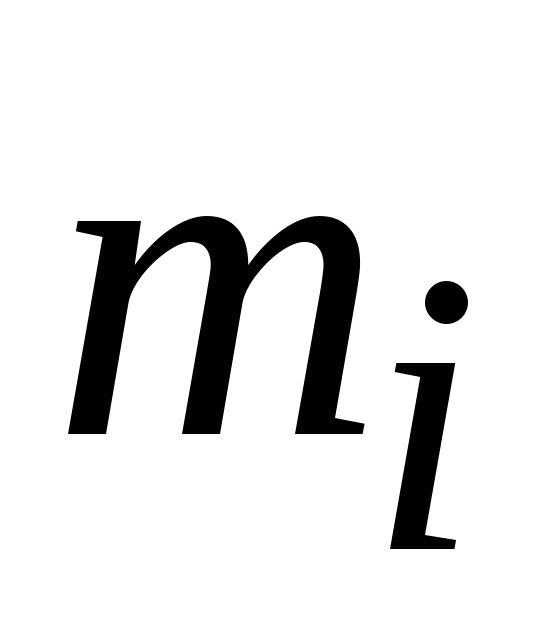
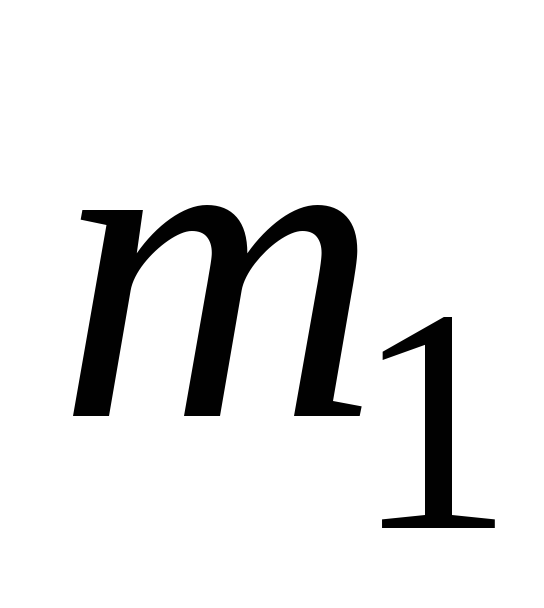
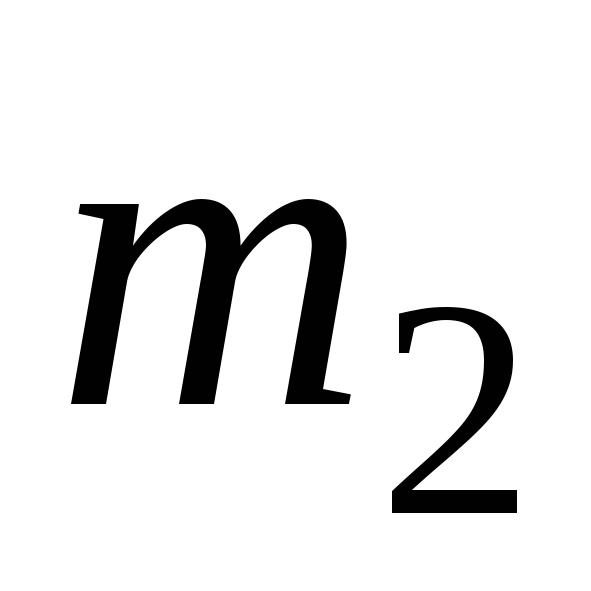
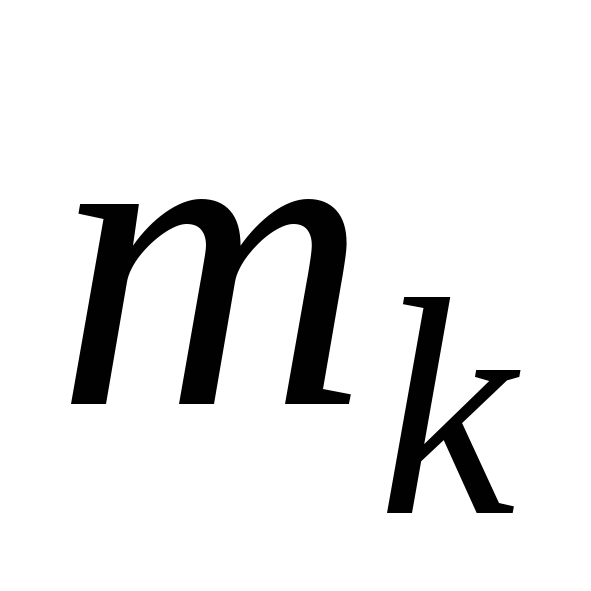
где
![]() - частота появления признаков, равного
- частота появления признаков, равного
![]() .
.
Пример 1. Выборка: 5, 7, 8, 8, 9, 10, 10, 10, 2, 2, 2, 8, 2, 4. Это могут быть длины предложений, состоящие из 5, 7,…, 4 слов. Имеем вариационный ряд:
-
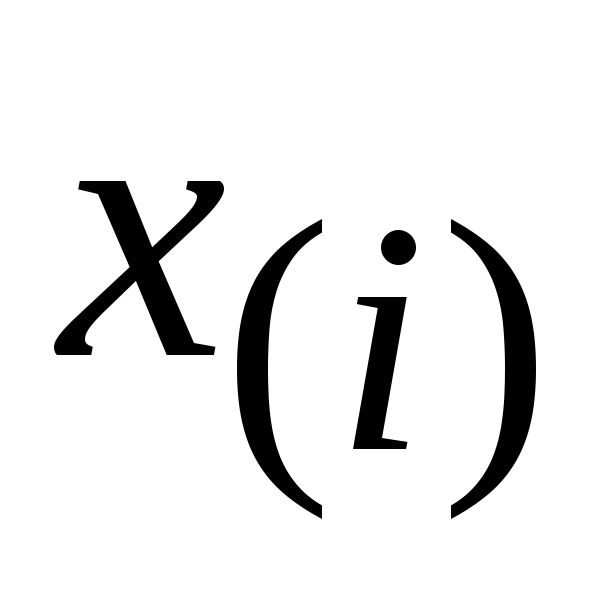
2
4
5
7
8
9
10
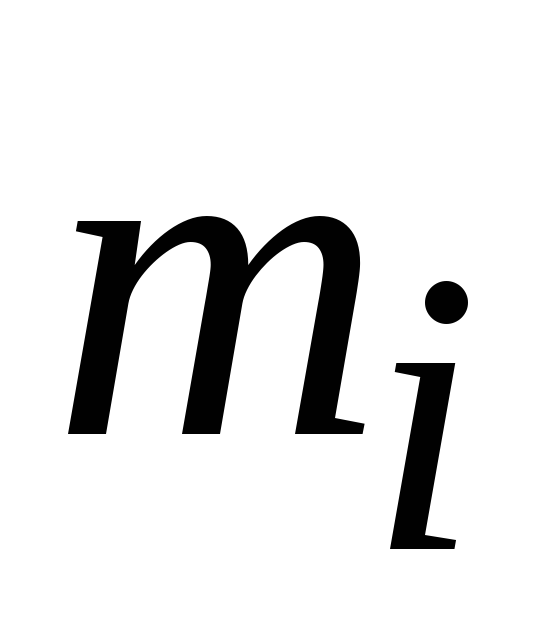
4
1
1
1
3
1
3
![]() 14.
14.
Пусть
![]() - дискретный изучаемый признак с
неизвестным распределением {
- дискретный изучаемый признак с
неизвестным распределением {![]() },
},
![]() .
.
Выше
мы сформулировали задачу установления
закона распределения признака
![]() .
Решим задачу в первом приближении.
Известно, что
.
Решим задачу в первом приближении.
Известно, что
![]() - относительная частота появления
- относительная частота появления
![]() ,
причем
,
причем
![]() ,
n
,
n![]() ,
т.е. при неограниченном числе наблюдений,
когда объем выборки стремится к объему
ГС. Итак, относительные частоты
,
т.е. при неограниченном числе наблюдений,
когда объем выборки стремится к объему
ГС. Итак, относительные частоты
![]() мы можем использовать для оценки в
первом приближении неизвестного закона
распределения изучаемого признака
мы можем использовать для оценки в
первом приближении неизвестного закона
распределения изучаемого признака
![]() ,
т.е. имеем
,
т.е. имеем
![]()
![]() .
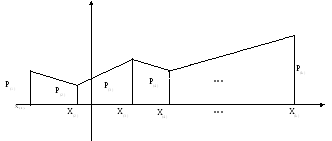
Графическое представление
.
Графическое представление
![]() есть полигон (многоугольник) относительных
частот.
есть полигон (многоугольник) относительных
частот.
Э тот
полигон есть оценка неизвестного
многоугольника вероятностей:
тот
полигон есть оценка неизвестного
многоугольника вероятностей:![]()
 Еще
раз: если бы мы могли просмотреть все
ГС, то сразу бы имели истинное распределение
признака
Еще
раз: если бы мы могли просмотреть все
ГС, то сразу бы имели истинное распределение
признака
![]() ,
но из-за невозможности делать это, мы
строим полигон относительных частот,
как приближенный вариант теоретического
(неизвестного) распределения
,
но из-за невозможности делать это, мы
строим полигон относительных частот,
как приближенный вариант теоретического
(неизвестного) распределения
![]() .
.
При
большом объеме выборки целесообразно
производить группировку данных. Для
этого область
![]() ,
где
,
где
![]() ,
,
![]() ,
разбивается на
,
разбивается на
![]() интервалов одинаковой длины
интервалов одинаковой длины
![]()
![]() и подсчитывается число элементов
и подсчитывается число элементов
![]() ,
попавших в
,
попавших в
![]() интервал. Наиболее простой способ
группирования состоит в следующем:
интервал. Наиболее простой способ
группирования состоит в следующем:
-
выбирается число интервалов
 ,
где
,
где
 - целая часть числа
- целая часть числа
 ;
; -
Определяется длина интервала
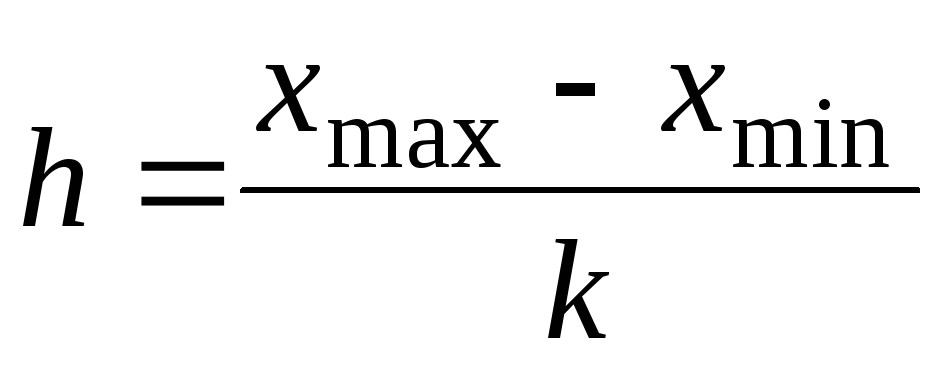 ,
причем
,
причем
 округляется в сторону увеличения.
округляется в сторону увеличения.
Тогда
![]() ,
тем самым учитываются все наблюдения
,
тем самым учитываются все наблюдения
![]() .
.
Такой
выбор
![]() ,
а, следовательно, и
,
а, следовательно, и
![]() наиболее эффективен, т.к. полученные
интервалы данной длины
наиболее эффективен, т.к. полученные
интервалы данной длины
![]() будут наиболее информативными.
будут наиболее информативными.
Далее строится функция:
![]()
 ,
при
,
при
![]() интервалу.
интервалу.
Ее называют гистограммой.
Очевидно,
![]()
Поскольку
![]() ,
то гистограмма есть оценка неизвестной
плотности
,
то гистограмма есть оценка неизвестной
плотности
![]() ,
задающей закон распределения непрерывного
признака
,
задающей закон распределения непрерывного
признака
![]() .
.
Можно построить гистограмму и для вариационного ряда:
-

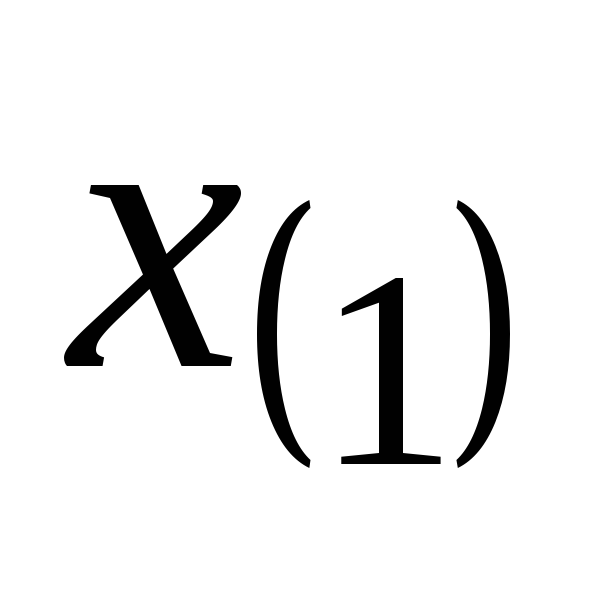
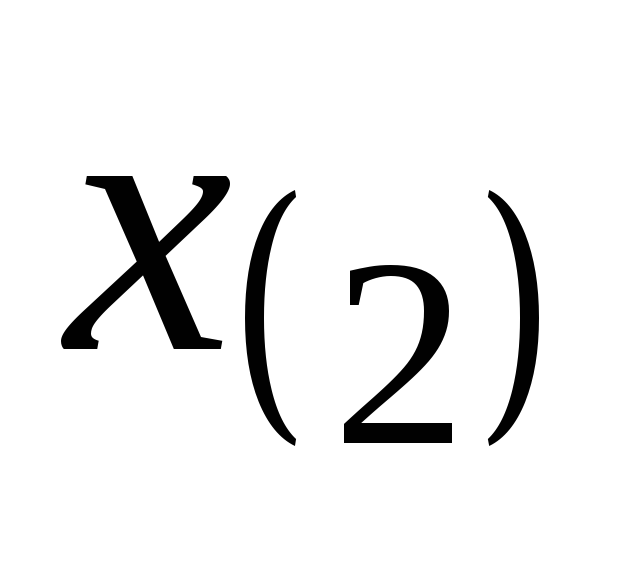
. . .
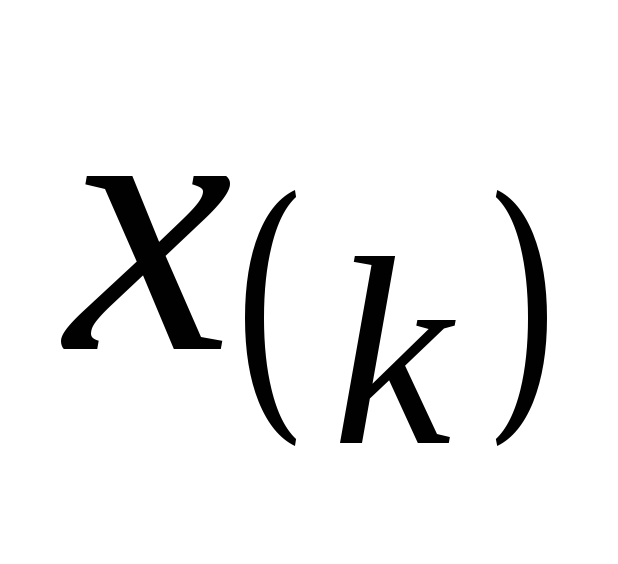

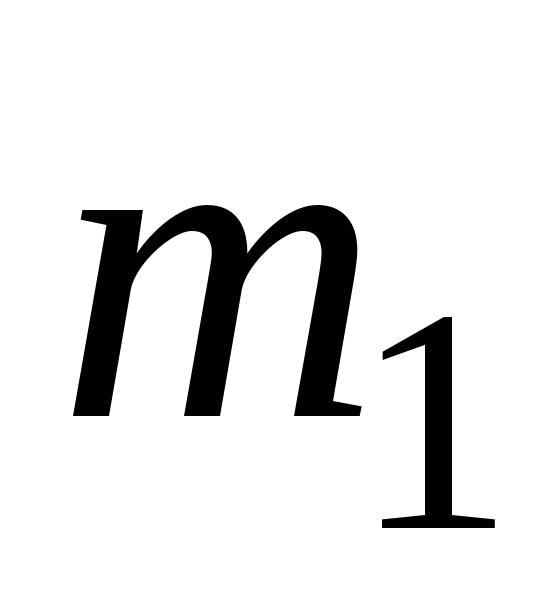
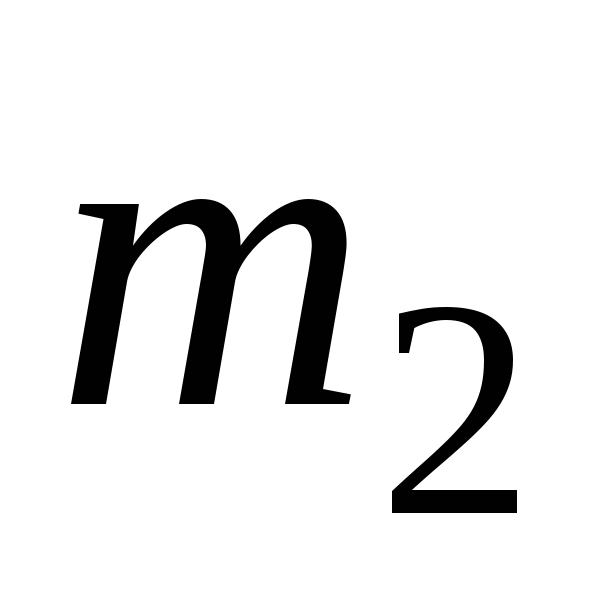
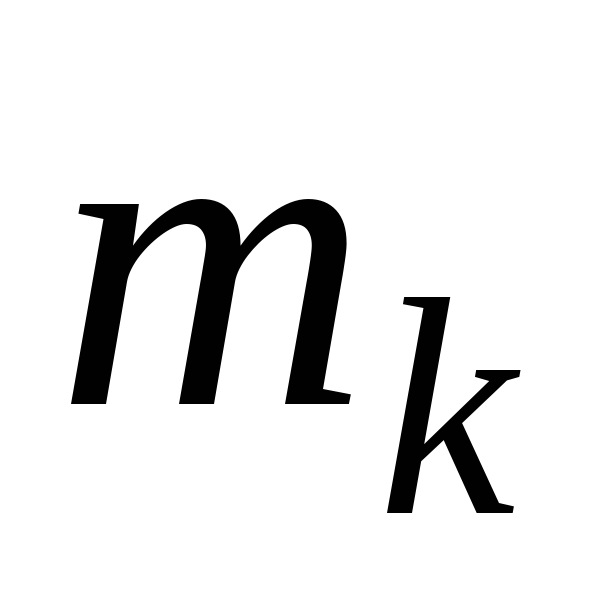
![]() .
.
Для этого строится функция
![]() ,
,
![]() ,
где
,
где
![]() .
Тогда имеем:
.
Тогда имеем:



Как правило, нас будет интересовать второй вид гистограммы, задающий оценку неизвестного распределения, т.к. мы в основном будем рассматривать дискретные признаки.
Пример
2 Дана
выборка: 2, 3, 3, 1, 4, 3, …, 0, 0, …, 6, 4, …, 1,7;
![]() .
.
Построим вариационный ряд:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
4 |
13 |
14 |
24 |
17 |
3 |
3 |
2 |
|
|
0.05 |
0.165 |
0.172 |
0.3 |
0.21 |
0.035 |
0.035 |
0.025 |
![]() 1.
1.
П олигон
относительных частот:
олигон
относительных частот:
Гистограмма:
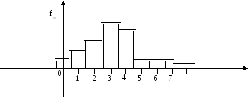
Вспомним,
что теоретическое распределение (которое
неизвестно для
![]() )
можно так же задать через
функцию распределения
)
можно так же задать через
функцию распределения
![]() :
ее вид однозначно задает распределение
признака
:
ее вид однозначно задает распределение
признака
![]() .
Поэтому задачу оценки теоретического
распределения можно решать, строя оценку
для
.
Поэтому задачу оценки теоретического
распределения можно решать, строя оценку
для
![]() .
Для этого используется эмпирическая
функция распределения (кумулята)
.
Для этого используется эмпирическая
функция распределения (кумулята)
![]() .
.

