Основы статистического анализа

1 Основные задачи статистического анализа

1.1 Выборочный метод

Основой статистического анализа является выборочный метод. Часто нет необходимости, а иногда и возможности обследования всех объектов изучаемой совокупности или всех исходов рассматриваемого явления. Даже в тех случаях, когда проводится обследование всех объектов совокупности, его можно рассматривать как выборку (например, перепись населения).

Главной задачей статистического анализа является описание общих закономерностей и характеристик всей совокупности (генеральной совокупности) на основе ограниченного числа наблюдений (выборки). Поэтому выборка должна достаточно полно и правильно отражать генеральную совокупность, то есть быть репрезентативной. Рассматривают два основных способа получения такой случайной выборки:

а) простой случайный отбор,

б) сложный случайный отбор.

В первом случае элементы выборки можно получить “разыгрывая” n элементов генеральной совокупности, например, с помощью датчика псевдослучайных чисел. Во втором случае вся генеральная совокупность разбивается на полсовокупности и из каждой осуществляется простой случайный отбор. Например, “Тихий Дон” М. Шолохова разбивается на 4 тома (4 полсовокупности). Такое построение выборки обеспечивает объективность данных. Часто выборка получается естественным образом как результат проведения соответствующего эксперимента (естественная выборка). При применении методов статистического анализа в языковых исследованиях рассматриваются как случайные выборки, так и естественные (реже).

1.2 Основные задачи статистического анализа

Основная задача статистического анализа в общем, виде может быть сформулирована следующим образом:

как на основе ограниченного числа наблюдений (выборки) описать основные закономерности, присущие генеральной совокупности.

У добно рассматривать всю генеральную совокупность (ГС) как множество всех значений изучаемого признака:

или : выборка.

Тогда задачи статистического анализа можно формализовать, рассматривая их как задачи относительно признака . Признак , как правило, может рассматриваться как случайная величина (с.в.), значение которой до опыта предсказать нельзя.

Задача 1

Установление теоретического распределения признака .

Если бы мы имели возможность посмотреть всю ГС, то знали бы все об изучаемом признаке (и о ГС). С.в. характеризуется, прежде всего, своим законом изменения (распределением вероятностей). Поэтому одна из основных задач состоит в установлении теоретического распределения с.в. на основе ограниченного объема наблюдений (т.е. по выборке).

Рассматривают два основных типа признаков (с.в.):

а) дискретные

б) непрерывные

Дискретные с.в. В этом случае признак принимает конечное или бесконечное (счетное) число значений: . Если мы каждому значению признака поставим в соответствии вероятность наблюдать это значение, то получим закон изменения признака (с.в.) :

			….
			….

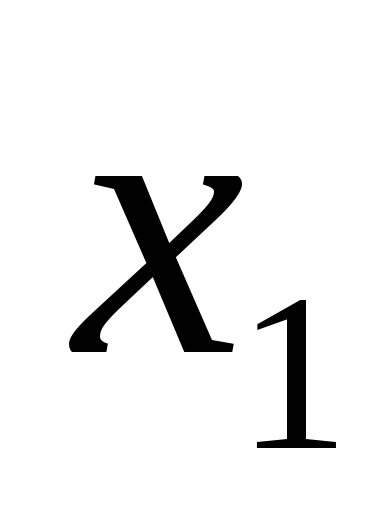
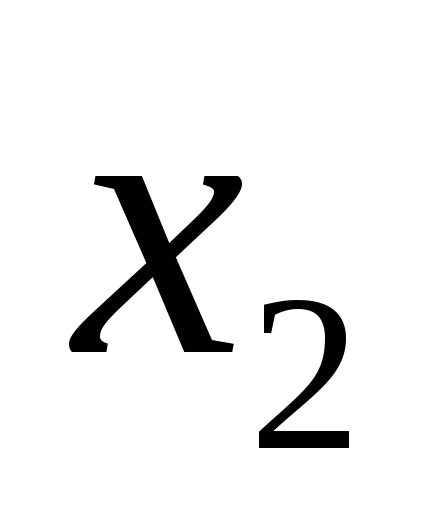
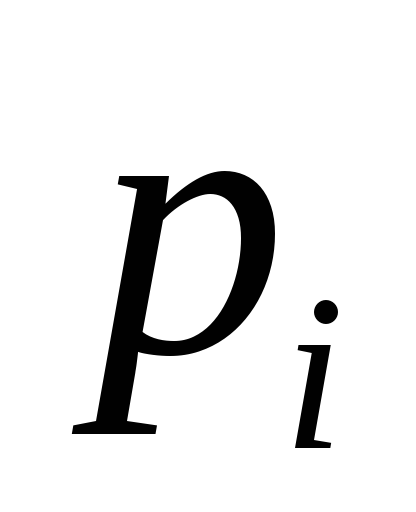
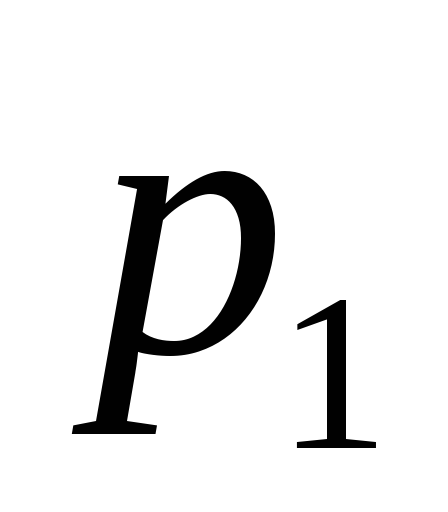
где