
- •Правила дифференцирования
- •6 Вопрос: Понятие первообразной функции и неопределенного интеграла, свойства.
- •7 Вопрос: Простейшие методы интегрирования.
- •8 Вопрос:Понятие определенного интеграла, св-ва.
- •9 Вопрос:Некоторые приложения интегрального исчисления:
- •10 Вопрос:Основные определения теории обыкновенных дифференциальных уравнений, прикладные задачи фармации, биологии, медицины.
- •Вопрос 21. Методы определения вязкости крови. Диагностическое значение вязкости крови.
- •Вопрос №22
- •Вопрос №23
- •Вопрос 24. Уравнение и характеристики механических свободных (затухающих и незатухающих) и вынужденных колебаний.
- •Вопрос 25. Уравнение и характеристики механической волны.
- •26. Эффект Доплера и его использование для медико-биологических исследований.
- •27. Звуковые колебания и волны.
- •28. Характеристики слухового ощущения и их связь с физическими характеристиками звука.
- •29. Физические основы звуковых методов исследования в клинике.
- •30. Когерентные источники. Интерференция света.
- •46. Полное сопротивление в цепи переменного тока.
- •47.Импеданс тканей. Физические основы реографии.
- •48. Электическое поле , его характеристики.
- •49.Физические основы электрокардиографии
9 Вопрос:Некоторые приложения интегрального исчисления:
Интегральное исчисление-раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения. И. и. тесно связано с дифференциальным исчислением и составляет вместе с ним одну из основных частей математического анализа (или анализа бесконечно малых). Центральными понятиями И. и. являются понятия определённого интеграла и неопределённого интеграла функций одного действительного переменного.
Приложения интегрального исчисления. Вычисление площадей
F
- площадь криволинейной трапеции,
ограниченной линиями y = 0, x = a, x = b и y =
f(x), где f(x) - непрерывная, положительная
функция, выраженная формулой
![]()
![]() .
Приведем два примера применения этой
формулы.
.
Приведем два примера применения этой
формулы.
Пример
1. Так как уравнение окружности (см. Рис.
1) с центром в начале координат и радиусом
R есть x2 + y2 = R2, то уравнение верхней
полуокружности имеет вид
![]()
![]()
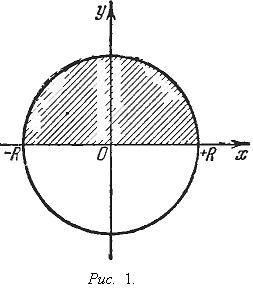
Поэтому площадь заштрихованного на чертеже полукруга равна
![]() .
.
Полагая x = R sin t, приводим этот интеграл к виду. Поэтому площадь всего круга равна πR2.
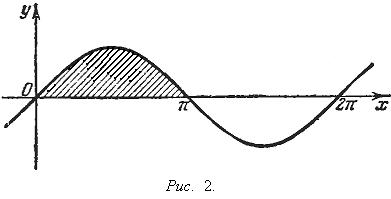
Пример 2. Рассмотрим площадь фигуры, ограниченной осью Ox и полуволновой синусоиды y = sin x (см. Рис. 2). Очевидно, эта площадь.
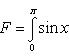
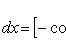
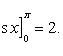
Любопытно, что она выразилась без каких бы то ни было иррациональностей.
Рассмотрим теперь площадь F фигуры, содержащейся между линиями x = a, x = b, y = f(x), y = g(x), где f(x) и g(x) - две непрерывные, положительные* функции, заданные на [a, b] и удовлетворяющие неравенству f(x) < g(x) (см. Рис. 3).
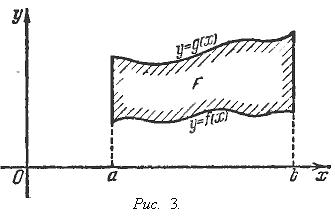
Вполне
очевидно, что эта площадь выражается
формулой
![]() -f(x)]dx
или , если положить g(x) - f(x) = r(x),
формулой
-f(x)]dx
или , если положить g(x) - f(x) = r(x),
формулой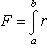 (х)d(x).
Последняя формула показывает, что форма
фигуры никакой роли не играет. Важна
лишь длина r(x) отрезка ординаты между
линиями y = f(x) и y = g(x). Отсюда следует,
что, взяв другую пару функций f1(x) и g1(x),
подчиненную условию g1(x) - f1(x) = r(x), мы
получим фигуру, равновеликую прежней.
Этот результат, установленный еще в
XVII в. одним из предшественников Ньютона
и Лейбница итальянцем Кавальери,
допускает и чисто геометрическую
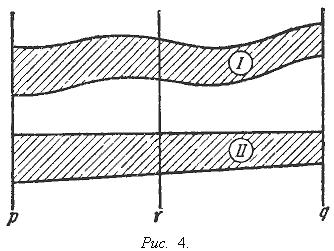
формулировку:Принцип Кавальери. Если
две плоские фигуры I и II содержатся между
двумя параллельными прямыми p и q (см.
Рис. 4) и обладают тем свойством, что в
сечении их любой прямой r, параллельной
p и q, получаются отрезки одинаковой
длины, то эти фигуры имеют одну и ту же
площадь.
(х)d(x).
Последняя формула показывает, что форма
фигуры никакой роли не играет. Важна
лишь длина r(x) отрезка ординаты между
линиями y = f(x) и y = g(x). Отсюда следует,
что, взяв другую пару функций f1(x) и g1(x),
подчиненную условию g1(x) - f1(x) = r(x), мы
получим фигуру, равновеликую прежней.
Этот результат, установленный еще в
XVII в. одним из предшественников Ньютона
и Лейбница итальянцем Кавальери,
допускает и чисто геометрическую
формулировку:Принцип Кавальери. Если
две плоские фигуры I и II содержатся между
двумя параллельными прямыми p и q (см.
Рис. 4) и обладают тем свойством, что в
сечении их любой прямой r, параллельной
p и q, получаются отрезки одинаковой
длины, то эти фигуры имеют одну и ту же
площадь.
10 Вопрос:Основные определения теории обыкновенных дифференциальных уравнений, прикладные задачи фармации, биологии, медицины.
Дифференциальные уравнения- уравнения, содержащие искомые функции, их производные различных порядков и независимые переменные. Теория Д. у. возникла в конце 17 в. под влиянием потребностей механики и других естественнонаучных дисциплин, по существу одновременно с интегральным исчислением и дифференциальным исчислением. Простейшие Д. у. встречались уже в работах И. Ньютона и Г. Лейбница; термин "Д. у." принадлежит Лейбницу
Обыкновенные дифференциальные уравнения. Уравнения 1-го порядка. Обыкновенным Д. у. 1-го порядка с одной неизвестной функцией называется соотношение F (x, у, у') = 0
между независимой переменной х, искомой функцией у и её производной.
Если уравнение (А) может быть разрешено относительно производной, то получается уравнение вида
y' = f (x, у). (Б)
Многие вопросы теории Д. у. проще рассматривать для таких разрешённых относительно производной уравнений, предполагая функцию f (x, y) однозначной.
Дифференциа́льное
уравне́ние
— уравнение, связывающее значение
некоторой неизвестной функции в некоторой
точке и значение её производных различных
порядков в той же точке. Дифференциальное
уравнение содержит в своей записи
неизвестную функцию, ее производные и
независимые переменные; однако не любое
уравнение, содержащее производные
неизвестной функции, является
дифференциальным уравнением. Например,
![]() не является дифференциальным уравнением.
Стоит также отметить, что дифференциальное
уравнение может вообще не содержать
неизвестную функцию, некоторые её
производные и свободные переменные, но
обязано содержать хотя бы одну из
производных.
не является дифференциальным уравнением.
Стоит также отметить, что дифференциальное
уравнение может вообще не содержать
неизвестную функцию, некоторые её
производные и свободные переменные, но
обязано содержать хотя бы одну из
производных.
Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.
Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y'(x),y''(x),...,y(n)(x) до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.
Обыкновенные дифференциальные уравнения
Обыкновенные
дифференциальные уравнения (ОДУ) — это
уравнения вида
![]()
или
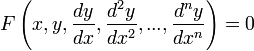
где
![]() — неизвестная функция (возможно,
вектор-функция; в таком случае часто
говорят о системе дифференциальных
уравнений), зависящая от независимой
переменной
— неизвестная функция (возможно,
вектор-функция; в таком случае часто
говорят о системе дифференциальных
уравнений), зависящая от независимой
переменной
![]() ,
штрих означает дифференцирование по
,
штрих означает дифференцирование по
![]() . Число
. Число
![]() называется порядком дифференциального
уравнения.
называется порядком дифференциального
уравнения.
2 часть вопроса:
1.Фармаци́я (греч. φάρμακον через кальку англ. pharmacy — лекарство и применение лекарств) — комплекс научно-практических дисциплин, изучающих проблемы создания, безопасности, исследования, хранения, изготовления, отпуска и маркетинга лекарственных средств, а также поиска природных источников лекарственных субстанций.
В комплексе с фармакологией составляет науку о лекарствах.
Основные разделы фармации
Фармация включает такие разделы, как фармацевтическая химия, технология фармацевтических препаратов и лекарственных форм, судебная химия, фармакогнозия, организация и экономика фармации, военная фармация и др.
К фармацевтическим учреждениям относятся:
научно-исследовательские институты
лаборатории и предприятия, изготовляющие лекарственные средства (фармацевтические заводы)
учреждения, ведающие сбором и обработкой лекарственных растений (заготовительные подразделения и фармфабрики)
аптеки и склады
контрольно-аналитические лаборатории.
Основными задачами медицинской службы являются:
1. поддержание в постоянной боевой и мобилизационной готовности сил и средств медицинской службы;
2. боевая подготовка и повышение профессионального уровня личного состава медицинской службы;
3. военно-медицинская подготовка личного состава войск, пропаганда гигиенических знаний и здорового образа жизни;
4. медицинское обеспечение учебно-боевой подготовки войск;
5. участие в обеспечении санитарно-эпидемиологического благополучия войск;
6. организация и проведение мероприятий по медицинской защите личного состава войск от воздействия неблагоприятных факторов окружающей среды, воинской службы и быта, сохранению и укреплению его здоровья, предупреждению возникновения и распространения заболеваний в войсках;
7. организация и проведение лечебно-профилактических мероприятий среди личного состава войск; оказание медицинской помощи больным, их лечение и медицинская реабилитация;
8. участие в комплектовании ВС РФ здоровым пополнением;
9. взаимодействие с органами управления и учреждениями здравоохранения, медицинской службой других министерств и ведомств.
Вопрос №11
Теоремы сложения и умножения. 1) пусть А и Б - два несовместных события, тогда вероятность их суммы равна сумме вероятностей слагаемых, т.е. Р(А+Б)=Р(А)+Р(Б) 2) пусть А и Б - два совместных события, тогда вероятность их суммы равна сумме вероятностей слагаемых без вероятности произведения, т.е. Р(А+Б)=Р(А)+Р(Б)-Р(АБ) Теоремы умножения: 3) пусть А и Б - два независимых события, тогда вероятность их произведения равна произведению вероятностей сомножителей, т.е. Р(АБ)=Р(А)Р(Б) 4) пусть А и Б - два зависимых события, тогда вероятность их произведения равна произведению вероятностей первого множителя на вероятность второго, вычисленную в предположении, что первое событие произошло (или вероятности второго множителя на вероятность первого, вычисленную в предположении, что второе событие произошло), т.е. Р(АБ)=Р(А)Р(Б/А)=Р(Б)Р(А/Б)
Если
событие
![]() может
наступить только при появлении одного
из несовместных событий (гипотез)
может
наступить только при появлении одного
из несовместных событий (гипотез)
![]() ,
то вероятность события
,
то вероятность события
![]() вычисляется
по формуле полной
вероятности:
вычисляется
по формуле полной
вероятности:
![]() ,
где
,
где
![]() -
вероятность гипотезы
-
вероятность гипотезы
![]() ,
,
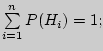
![]() -
условная вероятность события
-
условная вероятность события
![]() при
выполнении гипотезы
при
выполнении гипотезы
![]() (
(
![]() .
.
С
формулой полной вероятности тесно
связана формула Байеса. Если до опыта
вероятности гипотез были
![]() ,
,
![]() ,
...,
,
...,
![]() ,
а в результате опыта появилось событие
,
а в результате опыта появилось событие
![]() ,
то с учетом этого события "новые",
т.е. условные вероятности гипотез
вычисляются по формуле Байеса
,
то с учетом этого события "новые",
т.е. условные вероятности гипотез
вычисляются по формуле Байеса
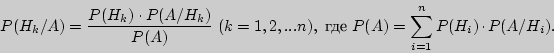
Формула
Байеса дает возможность "пересмотреть"
вероятность гипотез с учетом наблюдавшегося
результата опыта. Условная вероятность
![]() может
находиться как отношение веса ветви,
проходящей через вершину, соответствующую
гипотезе
может
находиться как отношение веса ветви,
проходящей через вершину, соответствующую
гипотезе
![]() ,
к весу всего вероятностного го
,
к весу всего вероятностного го
Теория вероятности – математическая наука, изучающая закономерности случайных явлений.
Теория вероятности изучает случайные события и случайные величины.
Случайное событие – это любой факт, который в результате испытания может произойти или не произойти.
Испытание (опыт, эксперимент) в этом определении понимается, как выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат. Испытание может проводиться человеком, но может осуществляться и независимо от человека. Человек в этом случае выступает в роли наблюдателя.
Событие обозначается прописными (заглавными) буквами латинского алфавита A,B,C.
-
Достоверное событие – если в результате испытания оно обязательно должно произойти.
-
Невозможное событие – если в результате испытания оно вообще не может произойти.
События называются несовместными, если наступление одного из них исключает появление другого. В противном случае события – совместные.
Противоположные события – два события А и А1 называются противоположными, если непоявление одного из них в результате данного испытания влечёт появление другого.
Вопрос №12
ЗАКОН ГАУССА, общий ЭЛЕКТРОМАГНИТНЫЙ ПОТОК над замкнутой поверхностью равен ЭЛЕКТРИЧЕСКОМУ ЗАРЯДУ внутри этой поверхности, разделенному на ДИЭЛЕКТРИЧЕСКУЮ ПРОНИЦАЕМОСТЬ среды
Применение?
Вопрос №13
Генеральная совокупность- это множество всех мыслимых значений наблюдений ( объектов), однородных относительно некоторого признака ,которые могли быть сделаны. Число всех наблюдений , составляющих генеральную совокупность, называется её объемом N.
Выборка- это совокупность случайно отобранных наблюдений( объектов). Объем выборки n.
Выборка обязательно должна удовлетворять условию репрезентативности, т.е. давать обоснованное представление о генеральной совокупности. Каждый элемент выборки Xi называется вариантой. Число наблюдений варианты ni называется частотой встречаемости. Последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом.
Статистическое распределение – это совокупность вариант Xi и соответствующих им частот ni.
Вопрос №14
Точечная оценка – это оценка, которая определяется одним числом. И это число определяется по выборке. Это функция результатов выборки.
Качество оценки устанавливается по трём свойствам: быть состоятельной, эффективной и несмещенной.
Точечная оценка называется состоятельной, если при увеличении объема выборки выборочная характеристика стремится к соответствующей характеристике генеральной совокупности.
Точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с другими аналогичными оценками.
Точечную оценку называют несмещённой, если её математическое ожидание равно оцениваемому параметру при любом объеме выборки.
Интервальная оценка – это числовой интервал, который определяется двумя числами - границами интервала, содержащий неизвестный параметр генеральной совокупности.
Доверительный интервал – это интервал, в котором с той или иной заранее заданной вероятностью находится неизвестный параметр генеральной совокупности.
Доверительная вероятность p – это такая вероятность, что событие вероятности 1-p можно считать невозможным. Альфа=1-p – это уровень значимости. (обозначения могут быть любыми, часто обозначают наоборот). Обычно в качестве доверительных вероятностей используют вероятности, близкие к 1. Тогда событие, что интервал накроет характеристику, будет практически достоверным. Это p> или = 0,95, p> или = 0,99, p> или = 0,999.Эти вероятности признаны достаточными для уверенного суждения о генеральных параметрах на основании известных выборочных показателей.
Вопрос №15
Статистическая гипотеза – это любое предположение о виде неизвестного распределения или о параметрах известных распределений. Статистическая гипотеза – это всякое высказывание о генеральной совокупности, проверяемое по выборке.
Гипотезы будем обозначать буквой H с индексом. Будем предполагать, что у нас имеется 2 непересекающихся гипотезы H0 b H1. H0 – нулевая гипотеза ( или основная). H1 – альтернативная или конкурирующая гипотеза.
Задача проверки статистических гипотез состоит в том, чтоб на основе выборки X1, X2, X3, … Xn принять (т.е. считать справедливой) либо нулевую гипотезу H0, либо конкурирующую гипотезу H1.
Для проверки принятой гипотезы используют статистический критерий – это правило , позволяющее, основываясь только на выборке x1, x2,x3,….,xn,принять либо отвергнуть нулевую гипотезу H0. Различают два вида критериев: параметрические и непараметрические.
Параметрические критерии представляют собой функции параметров данной совокупности и используются, если совокупности , из которых взяты выборки, подчиняются нормальному закону распределения.
Непараметрические критерии применяются, если нет подчинения нормальному закону.
Вопрос №16. Понятие функциональной зависимости
Будем говорить, что между двумя признаками X и Y существует функциональная зависимость (взаимосвязь), при которой каждому значению одного из них соответствует одно или несколько строго определенных значений другого.
Например,
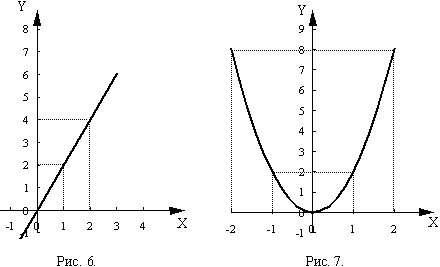
в функции у = 2 * х каждому значению х соответствует
в два раза большее значение у .
В функции ![]() каждому
значению усоответствует
2 определенных значения х .
Графически это выглядит так (рис. 6, 7
соответственно):
каждому
значению усоответствует
2 определенных значения х .
Графически это выглядит так (рис. 6, 7
соответственно):
 Понятие
корреляционной зависимости и ее
направленности
Понятие
корреляционной зависимости и ее
направленности
Будем говорить, что между двумя признаками Х и У существует корреляционная зависимость (взаимосвязь), при которой с изменением одного признака изменяется и другой, но каждому значению признака Х могут соответствовать разные, заранее непредсказуемые значения признака У, и наоборот.
Для различия направленности влияния одного признака на другой введены понятия положительной и отрицательной связи.
Если с увеличением (уменьшением) одного признака в основном увеличиваются (уменьшаются) значения другого, то такая корреляционная связь называется прямой или положительной.
Если с увеличением (уменьшением) одного признака в основном уменьшаются (увеличиваются) значения другого, то такая корреляционная связь называется обратной или отрицательной.
Вопрос №17. Регрессио́нный (линейный) анализ — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X1,X2,...,Xp. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимыхи независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.
Цели регрессионного анализа
-
Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными)
-
Предсказание значения зависимой переменной с помощью независимой(-ых)
-
Определение вклада отдельных независимых переменных в вариацию зависимой
Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.
[править]Математическое определение регрессии
Строго регрессионную зависимость можно определить следующим образом. Пусть Y, X1,X2,...,Xp — случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений X1 = x1,X2 = x2,...,Xp = xp определено условное математическое ожидание
y(x1,x2,...,xp) = E(Y | X1 = x1,X2 = x2,...,Xp = xp) (уравнение линейной регрессии в общем виде),
то функция y(x1,x2,...,xp) называется регрессией величины Y по величинам X1,X2,...,Xp, а её график — линией регрессии Y по X1,X2,...,Xp, или уравнением регрессии.
Зависимость Y от X1,X2,...,Xp проявляется в изменении средних значений Y при изменении X1,X2,...,Xp. Хотя при каждом фиксированном наборе значений X1 = x1,X2 = x2,...,Xp = xpвеличина Y остаётся случайной величиной с определённым рассеянием.
Для выяснения вопроса, насколько точно регрессионный анализ оценивает изменение Y при изменении X1,X2,...,Xp, используется средняя величина дисперсии Y при разных наборах значений X1,X2,...,Xp (фактически речь идет о мере рассеяния зависимой переменной вокруг линии регрессии).
[править]Метод наименьших квадратов (расчёт коэффициентов)
На
практике линия регрессии чаще всего
ищется в виде линейной
функции Y = b0 + b1X1 + b2X2 +
... + bNXN (линейная
регрессия), наилучшим образом приближающей
искомую кривую. Делается это с
помощью метода
наименьших квадратов,
когда минимизируется сумма квадратов
отклонений реально наблюдаемых Y от их
оценок ![]() (имеются
в виду оценки с помощью прямой линии,
претендующей на то, чтобы представлять
искомую регрессионную зависимость):
(имеются
в виду оценки с помощью прямой линии,
претендующей на то, чтобы представлять
искомую регрессионную зависимость):
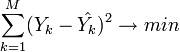
(M — объём выборки). Этот подход основан на том известном факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда Y = y(x1,x2,...xN).
Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки:

Условие минимума функции невязки:
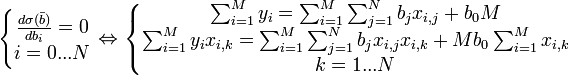
Полученная система является системой N + 1 линейных уравнений с N + 1 неизвестными b0...bN
Если представить свободные члены левой части уравнений матрицей
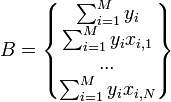
а коэффициенты при неизвестных в правой части матрицей
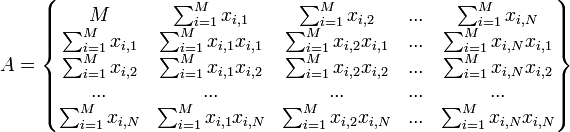
то
получаем матричное уравнение: ![]() ,
которое легко решается методом
Гаусса.
Полученная матрица будет матрицей,
содержащей коэффициенты уравнения
линии регрессии:
,
которое легко решается методом
Гаусса.
Полученная матрица будет матрицей,
содержащей коэффициенты уравнения
линии регрессии:

Для получения наилучших оценок необходимо выполнение предпосылок МНК (условий Гаусса−Маркова). В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators) − наилучшие линейные несмещенные оценки.
[править]Интерпретация параметров регрессии
Параметры bi являются частными коэффициентами корреляции; (bi)2 интерпретируется как доля дисперсии Y, объяснённая Xi, при закреплении влияния остальных предикторов, то есть измеряет индивидуальный вклад Xi в объяснение Y. В случае коррелирующих предикторов возникает проблема неопределённости в оценках, которые становятся зависимыми от порядка включения предикторов в модель. В таких случаях необходимо применение методов анализа корреляционного и пошагового регрессионного анализа.
Говоря о нелинейных моделях регрессионного анализа, важно обращать внимание на то, идет ли речь о нелинейности по независимым переменным (с формальной точки зрения легко сводящейся к линейной регрессии), или о нелинейности по оцениваемым параметрам (вызывающей серьёзные вычислительные трудности). При нелинейности первого вида с содержательной точки зрения важно выделять появление в модели членов вида X1X2, X1X2X3, свидетельствующее о наличии взаимодействий между признаками X1, X2 и т. д.
Вопрос №18. Смещение молекул в движущих слоях жидкости сопровождается действием сил сопротивления (Внутреннее трение). Оно характеризуется вязкостью h. Вязкость обусловлена межмолекулярным воздействием и зависит от природы жидкости и температуры. В жидких телах смещение молекул под действием внешних сил относительно друг друга происходит легко, поэтому упругих сил при сдвиге не возникает – текучесть. Ньютон установил, что сила внутреннего трения тем больше, чем больше площадь соприкосновения слоев и зависит от изменения скорости течения жидкости при переходе от слоя к слою.
Fтр=n![]() S
S
h - коэффициент внутреннего трения, вязкость.
dV/dX – градиент скорости – изменение скорости, отнесенное к расстоянию между слоями в направлении, перпендикулярном скорости.
S – площадь соприкосновения слоев.
Ньютоновские жидкости – если вязкость в силе трения зависит только от природы жидкости и температуры (вода, НМС, плазма крови, лимфа, бензол, Этиловый спирт).
Неньютоновские жидкости – если вязкость в силе трения зависит и от природы, температуры и от режима течения жидкости (эмульсии, суспензии, ВМС, кровь, протоплазма). h¹const.
Пуазейль установил, что средняя скорость (υср) ламинарного течения жидкости по круглой трубе постоянного сечения прямо пропорционально градиету давления:
P1- P2
l , квадрату радиуса трубы (r 2) и обратно пропорционально вязкости жидкости ( η );
υср.= P1 – P 2 r 2 , где
l 8η
P1 и P 2 – давления в начале и конце трубы , длиной l . υ сред. Течения жидкости определяет кол-во жидкости, протекающей через поперечное сечение S в ед-цу времени:
Q = υср. S, S = πr2
Формула Пуазейля
Q= P1 – P 2 π r 4 или Q= P1 – P 2 , где
l 8η ω
ω=8lη/πr4 – гидравлическое сопротивление возрастает с уменьшением радиуса трубы.
Падение давления Δ P= P1-P2 вдоль отдельной трубы, определяемое формулой Пуазейля; затем в виде P1-P2 =Qω, ω- гидравлическ.сопрот-е., т.е. при фиксированном объеме Q протекающей жидкости ΔP зависит от ω. В кровеносной системе падение давления вдоль кроветока зависит от гидравлического сопротивления разветвления, которое нах –ся по формулам для послед – го и парал.-го соед.-ний;
ω = ω1+ ω2+… +ωn – посл.соед.-е.
ω= ( 1 +1 +…1 ) –1 - парал. соед.-е.
ω1 ω2 ωn
Здесь проведена аналогия с законом Ома: 1) гидравлическое сопротивление ω =электрич. сопротив-е. R. 2) разность давлений ΔР= разность потенциалов. 3) Q = сила тока J.
З.Ома: J(ампер или кулон/с) = ΔU /R ф.Пуазейля: Q(м3/с)=ΔP/ω
Вопрос №19. Закон Бернулли: в различных точках линии тока идеальной жидкости сумма статического, динамического и гидростатического давлений одинакова:
Формула: P+ρυ2/2+ρgh=const
-
Статическое давление –P возникает от работы сердца, не связано с движением жидкости.
-
Динамическое (скоростное) давление ρυ2/2 связано с кинетической энергией потока жидкости, проявляется при торможении жидкости.
Формула P+ρυ2/2=Pn ( полное давление)
- Гидростатическое давление - ρgh связано с потенциальной энергией и перепадом высот.
Статическое и гидростатическое давление по своему действию одинаковы, но гидростатическое давление распред. объема жидкости (130 мм.рт.ст. = Ргол. – Рниж.кон. при росте =180 см. стоя). В невесомости это давление отсутствует.
Вопрос №20. Турбулентное течение – вихревое. Возникает при увеличении v течения вязкой жидкости вследствие неоднородности давления по поперечн. сечению трубы. При турб. течении υ частиц в каждом месте беспрерывно и хаотически меняется.
Число Рейнольдса крит. =2300.
-
При Re < Re крит. (2300) => течение ламинарное.
-
При Re > Re крит. => турбулентное течение.
Re = r u d /η Re = ud /ν , где
-
r - плотность жидкости
-
u – скорость течения
-
d – диаметр трубы
-
h- вязкость жидкости. Измеряется в СИ – ( М2\с), в СГС ( стокс).
υ крит.= Re *(ν/ r)
- ν - кинематическая вязк. жидкости , r – радиус сосуда, Re - зависит от природы: Н2О – 2300; кровь – 1000.
Течение крови в артериях в норме является ламинарным, небольшая турбулентность возникает вблизи клапанов. При патологии, когда вязкость крови меньше нормы, Re > Re крит. 1000 => движение турбулентное.
Турбулентное течение связано с дополнительной работой сердца à шум, возникающий при турбулентном течении крови à диагностика заболеваний.
Причины перехода ламинарного течения крови в турбулентное:
-
отложение холестерина на стенках сосуда (шум на дуге аорты)
-
врожденное отверстие в межжелудочковой перегородке (шумы в плеч.аорте).
-
множественные раветвления.
