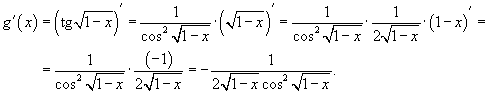- •Правила дифференцирования
- •6 Вопрос: Понятие первообразной функции и неопределенного интеграла, свойства.
- •7 Вопрос: Простейшие методы интегрирования.
- •8 Вопрос:Понятие определенного интеграла, св-ва.
- •9 Вопрос:Некоторые приложения интегрального исчисления:
- •10 Вопрос:Основные определения теории обыкновенных дифференциальных уравнений, прикладные задачи фармации, биологии, медицины.
- •Вопрос 21. Методы определения вязкости крови. Диагностическое значение вязкости крови.
- •Вопрос №22
- •Вопрос №23
- •Вопрос 24. Уравнение и характеристики механических свободных (затухающих и незатухающих) и вынужденных колебаний.
- •Вопрос 25. Уравнение и характеристики механической волны.
- •26. Эффект Доплера и его использование для медико-биологических исследований.
- •27. Звуковые колебания и волны.
- •28. Характеристики слухового ощущения и их связь с физическими характеристиками звука.
- •29. Физические основы звуковых методов исследования в клинике.
- •30. Когерентные источники. Интерференция света.
- •46. Полное сопротивление в цепи переменного тока.
- •47.Импеданс тканей. Физические основы реографии.
- •48. Электическое поле , его характеристики.
- •49.Физические основы электрокардиографии
Вопрос №1
Существует всего пять типов элементарных функций:
-
Степенные:
-
Линейная функция y = kx + b.
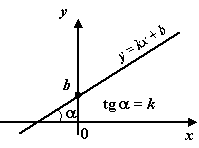
-
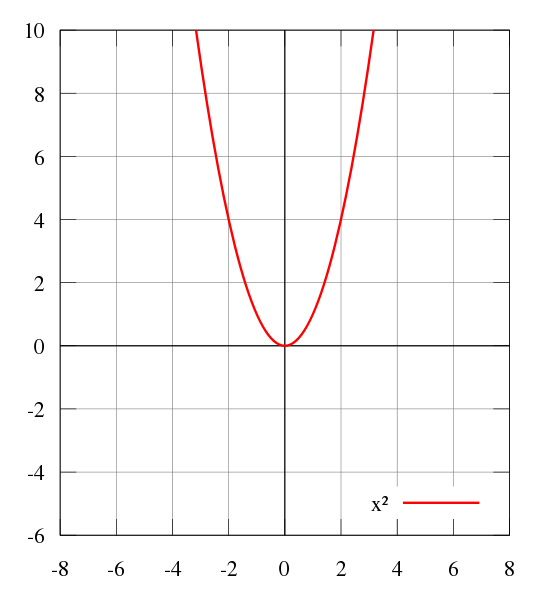
Квадратичная (график – парабола)
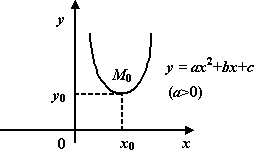
-
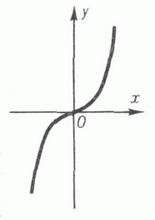
Нечётные степенные ф-ции (y=x3, y=x5, y=x7…)
-
Чётные степенные ф-ции (y=x2, y=x4, y=x8…)
-
Гипербола (y=1/x)
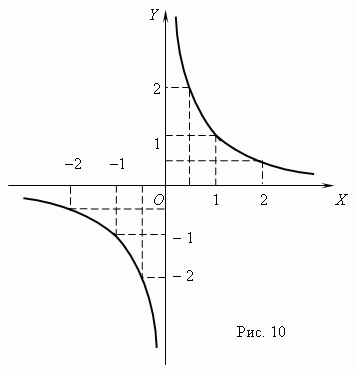
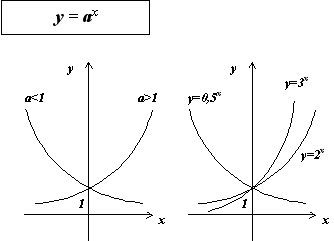
2.Показательные (y=ax) a>0 (a не равно 1)
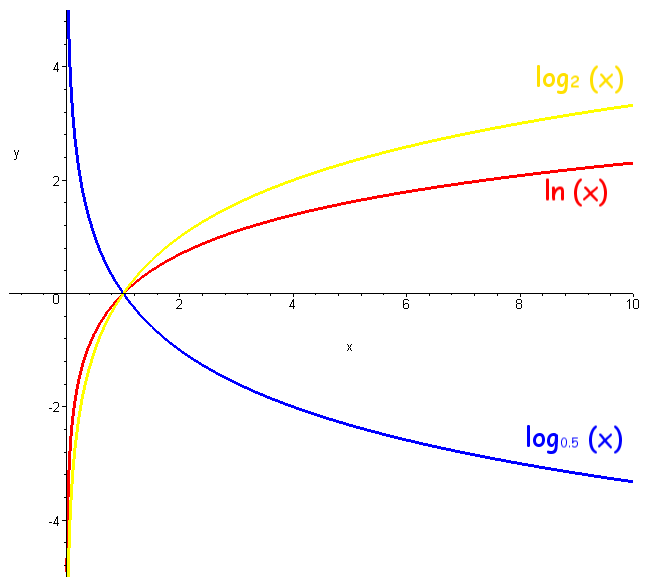
3.Логарифмические (y=logax)
4. Тригонометрические
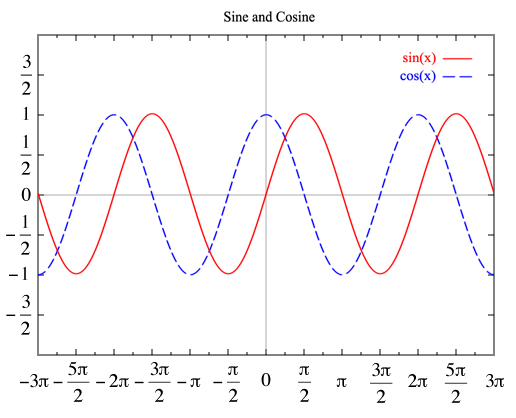
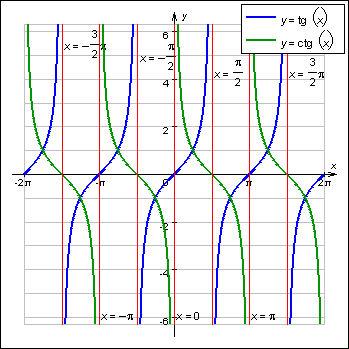
5. Обратные тригонометрические.
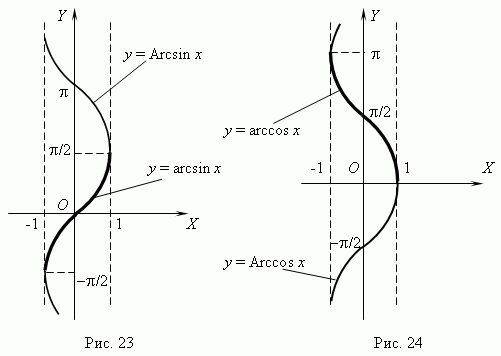
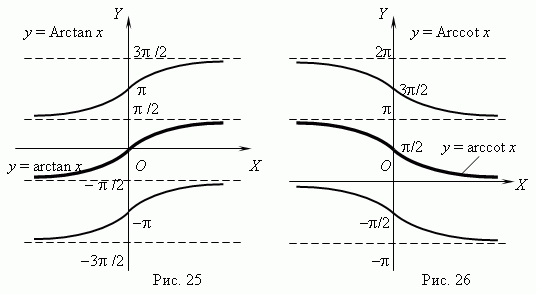
6. Многочлен
Это
функция вида ![]() ,
где
,
где ![]() ,
, ![]()
Чётные многочлены (n-чётное число):
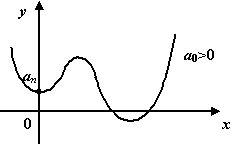
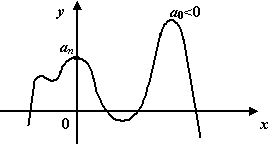 Нечётные
многочлены (n-нечётное
число):
Нечётные
многочлены (n-нечётное
число):
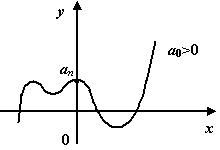
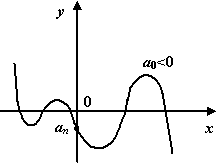 http://studrus.ru/stud39/ris/image115.pngC:\Documents
and Settings\Admin\Мои
документы\Downloads\fun9o.gif
http://studrus.ru/stud39/ris/image115.pngC:\Documents
and Settings\Admin\Мои
документы\Downloads\fun9o.gif
Вопрос №2
Преде́л
фу́нкции (предельное
значение функции) в
заданной точке, предельной для
области определения функции, — такая
величина, к которой стремится
рассматриваемая функция при
стремлении её аргумента к данной точке
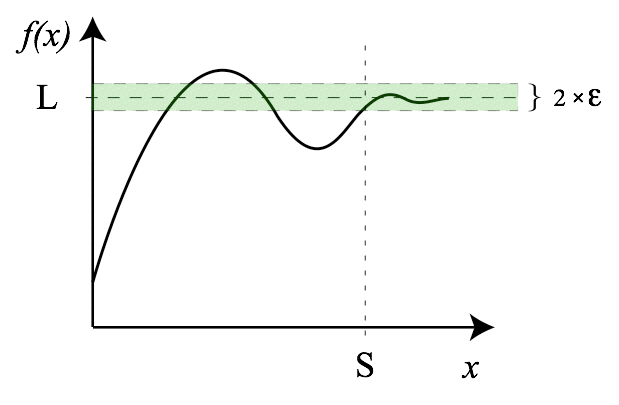
Теоремы о пределах.
Теорема. 1. Предел суммы есть сумма пределов.
Теорема. 2. Предел произведения есть произведение пределов.
Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).
Теорема. 4. Если u(x) z(x) v(x), и limx a u(x)=limx a v(x)=b, то limx a z(x)=b. ("Теорема о двух милиционерах").
Вопрос №3
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием.
Если
существует
![]() ,
то этот предел называется производной
функции y=f(x)
,
то этот предел называется производной
функции y=f(x)
y ' =
![]() =
=
Геометрический смысл производной:
Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
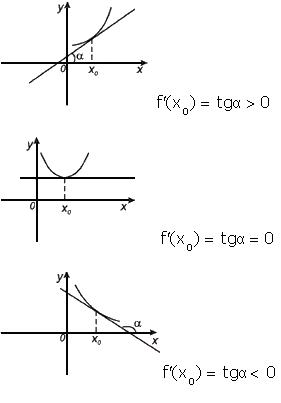
![]()
Физический смысл производной:
риведем несколько примеров.
-
Среднее ускорение материальной точки выражается формулой a=
 tv(t+
tv(t+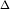 t)−v(t)
t)−v(t)
Мгновенное
ускорение точки равно a=lim![]() t
t![]() 0
0![]() tv(t+
tv(t+![]() t)−v(t)=dtdv=v
t)−v(t)=dtdv=v![]()
-
Сила и импульс по второму закону Ньютона связаны соотношением F=dtdp=p
 .
. -
Количество заряда, прошедшего через поперечное сечение проводника, определяет силу тока: I=dtdq=q
 .
. -
В электростатическом поле, изменяющемся только по оси OX, напряженность и потенциал связаны соотношениемE=−dxd
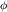 =−
=−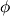
 .
.
Вопрос №4
Правила дифференцирования
Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) (с) ' = 0, (cu) ' = cu';
2) (u+v)' = u'+v';
3) (uv)' = u'v+v'u;
4) (u/v)' = (u'v-v'u)/v2;
5)
если y = f(u), u = (x), т.е. y = f((x)) - сложная
функция, или суперпозиция,
составленная из дифференцируемых
функций и f, то ![]() ,
или
,
или
На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.
1. (u)' = u1 u' ( принадлежит R1 )
2. (au)' = au lna u'.
3. (eu)' = eu u'.
4. (loga u)' = u'/(u ln a).
5. (ln u)' = u'/u.
6. (sin u)' = cos u u'.
7. (cos u)' = - sin u u'.
8. (tg u)' = 1/ cos2u u'.
9. (ctg u)' = - u' / sin2u.
10.
(arcsin u)' = u' /![]() .
.
11.
(arccos u)'
= - u' /![]() .
.
12. (arctg u)' = u'/(1 + u2).
13. (arcctg u)' = - u'/(1 + u2).
Вопрос №5 Правило дифференцирования сложной функции
Сложная
функция (композиция
функций, суперпозиция
функций)
обозначается ![]()
Производная композиции равна:
![]()
Если необходимо взять производную от композиции трех и более функций, то последовательно применяем указанное выше правило. Например,
|
Пример 1 |
|
|
|
Найти
производную функции Решение. Поскольку |
|
Пример 2 |
|
|
|
Найти
производную функции Решение. Здесь
мы имеем дело с композицией трех
функций. Производная тангенса равна |
6 Вопрос: Понятие первообразной функции и неопределенного интеграла, свойства.
Первообразная
Первообра́зной или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Так,
например, функция
![]() является первообразной
является первообразной
![]() . Так как производная константы равна
нулю, будет иметь бесконечное количество
первообразных; таких как или … и т. д.;
таким образом семейство первообразных
функции x2 можно обозначить как F(x) = x3 /
3 + C, где C — любое число. Графики таких
первообразных смещены вертикально
относительно друг друга , и их положение
зависит от значения C.
. Так как производная константы равна
нулю, будет иметь бесконечное количество
первообразных; таких как или … и т. д.;
таким образом семейство первообразных
функции x2 можно обозначить как F(x) = x3 /
3 + C, где C — любое число. Графики таких
первообразных смещены вертикально
относительно друг друга , и их положение
зависит от значения C.
Первообразные
важны тем, что позволяют вычислять
интегралы. Если F — первообразная
интегрируемой функции f, то:
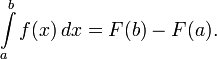
Это соотношение называется формулой Ньютона — Лейбница.
Благодаря
этой связи множество первообразных
данной функции f называют неопределённым
интегралом (общим интегралом) f и
записывают в виде интеграла без указания
пределов:
![]()
Если F — первообразная f , и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.
Каждая
непрерывная функция f имеет первообразную
F, одна из которых представляется в виде
интеграла от f с переменным верхним
пределом:
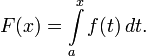
Также
существуют разрывные функции, которые
имеют первообразную. Например,
![]() с f(0) = 0 не непрерывна при x = 0, но имеет
первообразную
с f(0) = 0 не непрерывна при x = 0, но имеет
первообразную
![]() с F(0) = 0.
с F(0) = 0.
Некоторые
первообразные, даже несмотря на то, что
они существуют, не могут быть выражены
через элементарные функции (такие как
многочлены, экспоненциальные функции,
логарифмы, тригонометрические функции,
обратные тригонометрические функции
и их комбинации). Например:
![]()
Свойства первообразной:
1.Первообразная суммы равна сумме первообразных
2.Первообразная произведения константы и функции равна произведению константы и первообразной функции
3.Достаточным условием существования первообразной у заданной на отрезке функции f является непрерывность f на этом отрезке
4.Необходимыми условиями существования являются принадлежность функции f первому классу Бэра и выполнение для неё свойства Дарбу
5.У заданной на отрезке функции любые две первообразные отличаются на постоянную.
Если
принять во внимание тот факт, что
производная от константы С равна нулю,
то справедливо равенство
![]() . Таким образом, функция f(x) имеет множество
первообразных F(x)+C, для произвольной
константы С, причем эти первообразные
отличаются друг от друга на произвольную
постоянную величину.
. Таким образом, функция f(x) имеет множество
первообразных F(x)+C, для произвольной
константы С, причем эти первообразные
отличаются друг от друга на произвольную
постоянную величину.
Определение неопределенного интеграла.
Все
множество первообразных функции f(x)
называется неопределенным
интегралом
этой функции и обозначается
![]() .
.
Выражение
![]() называют подынтегральным выражением,
а f(x) – подынтегральной функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
называют подынтегральным выражением,
а f(x) – подынтегральной функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной):
1.
![]()
1.Производная результата интегрирования равна подынтегральной функции.
2.
![]()
2.Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.
3.
![]() ,
где k – произвольная константа.
,
где k – произвольная константа.
3. Коэффициент можно выносить за знак неопределенного интеграла.
4. Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.
4.![]()
Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь: первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно; второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.
Таблица первообразных: