Геометрическая интерпретация.

Геометрическая интерпретация задач дает возможность наглядно представить их структуру, выявить особенности и открывает пути исследования более сложных свойств.

Пусть дана задача

(min) Z=C₁x₁+ C₂x₂ (2.49)

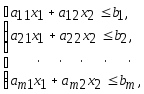(2.50)

õ₁0, õ₂0. (2.51)

Совокупность чисел õ₁, õ₂,...,õ_n, удовлетворяющих ограничениям называется решением. Если система неравенств (2.50) при условии (2.51) имеет хотя бы одно решение, она называется совместной, в противном случае несовместной. Дадим геометрическую интерпетацию элементов этой задачи. Каждое из ограничений задает на плоскости õ₁Îõ₂ некоторую полуплоскость с граничной прямой à_i1x₁+à_i2x₂=b_i (i=1,2,...,m). Полуплоскость — выпуклое множество. Но по лемме 1. пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи (2.49)—(2.51) есть выпуклое множество.

Условия неотрицательности определяют полуплоскости соответственно с граничными прямыми õ₁=0, õ₂=0. Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы. Совокупность этих точек (решений) назовем многоугольником решений. Он может быть точкой, отрезком, лучом, многоугольником, неограниченной многоугольной областью.

Таким образом, геометрическая задача линейного программирования представляет собой отыскание такой точки многогранника рещений, координаты которой доставляют линейной функции минимальное значение, причем допустимыми решениями служат все точки многогранника решений.

Перейдем к геометрической интерпретации целевой функции. Пусть область допустимых решений ЗЛП — непустое множество. Например многоугольник À₁À₂À₃À₄À₅À₆ (рис. 2.4). Выберем произвольное значение целевой функции Z=Z₀. Получим C₁x₁+ C₂x₂ =Z₀. Это уравнение прямой линии. В точках прямой NM целевая фунцция сохраняет одно и то жэе постоянное значение Z₀. Считая в равенстве (2.49) Z параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения).

2.6. Свойства решений задачи линейного программирования Свойства основной задачи линейного программирования.

Свойства основной задачи линейного программирования тесным образом связаны со свойствами выпуклых множеств.

Т е о р е м а 1. Множество всех планов задачи линейного программирования выпукло.

Доказательство. Необходимо доказать, что если Х₁ и Х₂ — планы задачи линейного программирования, то их выпуклая линейная комбинация Х=₁Х₁+₂Х₂, ₁  0, ₂  0, ₁+₂=1 также план задачи.

Так как Х₁ и Х₂ — планы задачи, то выполняются соотношения

АХ₁=А₀, Х₁  0, АХ₂=А₀, Х₂  0.

Перемножая

АХ= A(₁Х₁ +₂Х₂)= ₁АХ₁+ ₂АХ₂ =₁А₀+ ₂А₀=(₁+₂)А₀= А₀,

получаем, что Х удовлетворяет системе (2.43).

(2.52)

x_i  0 (i=1,2,..., n) (2.53)

Но так как Х₁  0; Х₂  0, ₁  0, ₂  0, то и Х  0, т. е. удовлетворяет и условию (2.53). Таким образом Х — план задачи линейного программирования.

Т е о р е м а 2. Линейная функция задачи линейного программирования достигает своего минимального значения в угловой точке многогранника рещений. Если линейная функция принимает минимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Доказательство. Предположим, что многогранник решений ограниченный, имеющий конечное число угловых точек. Обозначим его через К. В двумерном пространстве К имеет вид многоугольника, изображенного на рис. 2.5. Обозначим угловые точки К через Х₁, Х₂, ... , Х_p, а оптимальный план — через Х₀. Тогда Z(X₀) Z(X) для всех Х из К. Если Х₀ — угловая точка, то первая часть теоремы доказана. Предположим, что Х₀ не является угловой точкой; тогда Х₀ на основании теоремы 1 можно представить как выпуклую линейную комбинацию угловых точек К, т. е.

Х₀=₁Х₁+₂Х₂+ ... +_pХ_p, _i  0 (i= 1,2,..., p), .

Так как Z(X) — линейная функция, получаем

Z(X)=Z(₁Х₁+₂Х₂+ ... +_pХ_p) = ₁Z(X₁) +

+₂Z(X₂) + ... +_pZ(X_p). (2.54)

В этом разложении среди значений Z(X_i) (i=1,2,..., p) выберем наименьшее пусть оно соответствует угловой точке Х_k (1 k  p) и обозначим его через m, т. е. Z(X_k)=m. Заменим в (2.54) каждое значение Z(X_i) этим наименьшим значением. Тогда, так как _i  0 , , то

Z(X₀)  ₁m + ₂m + ... +_pm = m.

По предположению, Х₀ — оптимальный план, поэтому, с одной стороны, Z(X₀)  m, но с другой стороны, доказано, что Z(X₀)  m, значит, Z(X₀)=m=Z(X_k), где X_k — угловая точка. Итак, существует угловая точка X_k, в которой линейная функция принимает минимальное значение.

Для доказательства второй части теоремы допустим, что Z(X) принимает минимальное значение более чем в одной угловой точке, например в точках Х₁, Х₂, ... , Х_q , 1< q  p; тогда Z(X₁)=Z(X₂)= ... =Z(X_q)= m. Если Х — выпуклая линейная комбинация этих угловых точек:

Х=₁Х₁+₂Х₂+ ... +_qХ_q , _i  0 (i= 1,2,..., q), ,

то

Z(X)=Z(₁Х₁+₂Х₂+ ... +_qХ_q) = ₁Z(X₁) + ₂Z(X₂) + ... +_qZ(X_q)=₁m + ₂m + ... +_qm = m.

т. е. линейная функция Z принимает минимальное значение в произвольной точке Х, являющейся выпуклой линейной комбинацией угловых точек Х₁, Х₂, ... , Х_q .