9

Тема 22. Непрерывное и диадное вейвлет-преобразование Введение.

В систему Mathcad программные средства для работы с вейвлетами были введены одними из первых, но в ограниченной форме – только для прямого и обратного вейвлет-преобразования временных рядов вейвлетами Добеши db4. Дальнейшее развитие программного обеспечения выполнялось в рамках специальных пакетов расширения (сначала Numerie Recipes, а затем Wavelets Extension), которые инсталлируются в систему обычным порядком.

В настоящей теме рассматриваются непрерывное вейвлет-преобразование, выполняемое типовыми средствами в системе Mathcad вейвлетами произвольной формы, задаваемой пользователем, а также простое диадное вейвлет-преобразование вейвлетом Добеши db4.

22.1. Непрерывное вейвлет - преобразование.

Под непрерывным вейвлет-преобразованием (CWT), как правило, понимается преобразование сигналов и функций в аналитической форме. Однако при обработке физических данных на ЭВМ они представляются в дискретной форме - числовыми рядами результатов измерений. В принципе, если дискретизация выполнена корректно и максимальные частоты в данных не превышают частоты Найквиста, то всегда возможно восстановление аналоговой формы сигналов. Однако обработка данных в аналоговой форме аналитическими методами не имеет каких-либо преимуществ перед цифровыми методами. Практически, чаще используется замена аналитических методов дискретными аналогами с достаточно малым шагом дискретизации. Применительно к CWT, если нас интересует только анализ сигнала (без последующего его синтеза), то дискретизация может выполняться с любой частотой, даже не удовлетворяющей критерию Найквиста. Дискретный аналог CWT с достаточно малым шагом дискретизации данных по масштабу вейвлета и его сдвигам будем называть непрерывно-дискретным (CDWT).

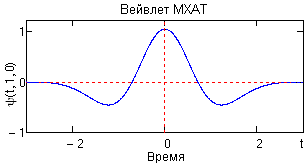
CWT типовыми средствами Mathcad. Качественный анализ сигналов, особенно модельных сигналов на основе гладких финитных функций, удобно производить симметричными аналитическими вейвлетами. Так, например, базовый вейвлет MXAT конструируется на основе второй производной функции Гаусса:

Отсюда:

_, (22.1.1)

где значения 'a' и 'b' – параметры масштаба вейвлета и сдвига, а значение коэффициента К определяется приведением нормы вейвлетной функции ||(t,a,b)|| к 1 при нулевом среднем значении:

t,a,b) dt  0, t,a,b)² dt  1.

Рис. 22.1.1.

Для MXAT-вейвлета значение К = 1.0314. Форма базового вейвлета при a=1 и b=0 приведена на рис. 22.1.1. Аналогично могут задаваться вейвлеты нечетного типа и вейвлеты любой другой формы.

Для демонстрации CWT зададим модельный сигнал в виде функции Гаусса на интервале 0-Т, Т=100 (рис. 22.1.2):

s(t) = 4 exp(-(t-50)²/10).

Рис. 22.1.2.

Формула прямого непрерывного вейвлет-преобразования представляет собой скалярное произведение сигнала и вейвлета:

S(a,b) = s(t), (t,a,b = s(t) t,a,b) dt. (22.1.2)

Если сигнал s(t) является финитным и выходит практически на нулевые значения по концам интервала задания, то пределы интегрирования в (22.1.2) можно задавать непосредственно по интервалу задания сигнала.

Для графического просмотра результатов преобразования следует задать шаг дискретизации функции S(a,b) по параметрам 'a', 'b' и выполнить дискретизацию. Например, для заданного интервала 0-Т функции s(t):

b = 1, i = 0..T, a = 0.5, j = 1..200, WS_i,j = S(ja, ib).

Графическое представление вейвлетного спектра сигнала в двух вариантах представлено на рис. 22.1.3.

Рис. 22.1.3.

Логарифмическая шкала масштабов. Вейвлетный спектр по шкале масштабов (обратна частотной шкале) удобно представлять в логарифмической шкале. Переход на логарифмическую шкалу (с определенным множителем) можно выполнять непосредственно при дискретизации сигнала S(a,b):

Спектр сигнала в логарифмической шкале масштабов приведен на рис. 2.1.4.

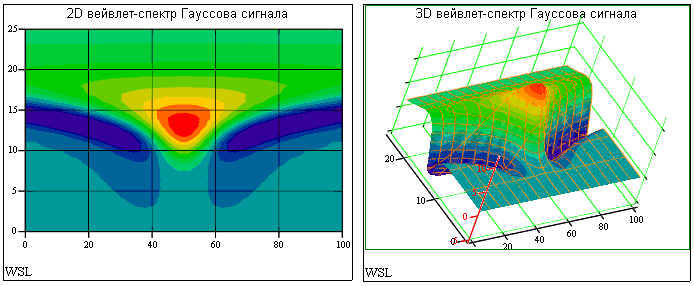
Рис. 22.1.4.

На рис. 22.1.5 приведен пример преобразования более сложного ЛЧМ сигнала.

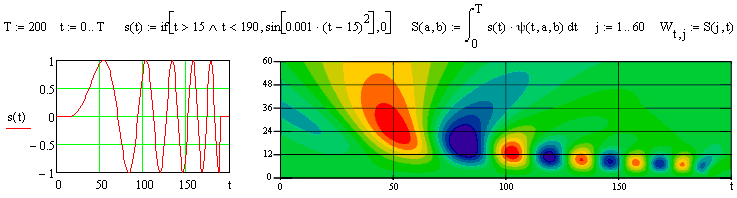
Рис. 22.1.5.

Рис. 22.1.6.

Связь шкалы масштабов с частотой. При практическом анализе частотных неоднородностей в сигнале масштабная шкала вейвлетного спектра несколько непривычна для визуального восприятия, но она всегда может быть заменена шкалой частот. Для перехода к шкале частот следует определить среднюю частоту вейвлета f₀ на единичном масштабе (а=1). Выполнить это можно непосредственно во временной области по максимуму функции взаимной корреляции:

p(f) = t,1,0) cos(2ft) dt.

После определения значения f₀ (рис. 22.1.6) частотная шкала вычисляется по масштабной шкале трансформацией f₀/a  f.

Рис. 22.1.7.

CDWT типовыми средствами Mathcad. При вычислении вейвлетных спектров в дискретной форме существенное значение для наглядности и выразительности спектров имеет шаг дискретизации параметров 'a' и 'b'. Шаг дискретизации b, как правило, принимается равным t анализируемых сигналов, т.е. равен 1, как и условное значение t, при этом временной масштаб вейвлетного спектра соответствует временному масштабу сигнала и удобен для локализации особенностей в сигнале.

Для обеспечения возможности изменения базового размера вейвлета в его формулу множителем к параметру 'a' вводится постоянный масштабный коэффициент 'd', как это показано на рис. 22.1.7 для вейвлета MXAT. Средняя частота спектра базового вейвлета при а=1 не должна превышать частоты Найквиста, но должна быть больше максимальной частоты в спектре сигнала.

Размер вейвлета в единицах t (целочисленные значения) задается параметром L. Так как значение L = 1 (размер вейвлета 2t) соответствует частоте Найквиста, а частота «короткой волны» в пределах этого размера будет больше частоты Найквиста, то минимальное значение L равно 2, что обеспечивает максимальную разрешающую способность по времени. Под это значение L и рекомендуется подобрать такое максимальное значение коэффициента ‘d’, при котором обеспечивается (с определенной точностью) выполнение условий:

t,1,0) dt  0, t,1,0)² dt  1. (2.1.3)

Сохранение найденного значения const = L∙d обеспечивает выполнение условий (2.1.3) для любой пары значений L и d. Минимальное значение L=2 действительно для CWT, но не рекомендуется для CDWT, т.к. дискретизация вейвлета порождает периодизацию его частотного спектра и перекрытие главного диапазона с боковыми, что наглядно видно на рис. 22.1.8.

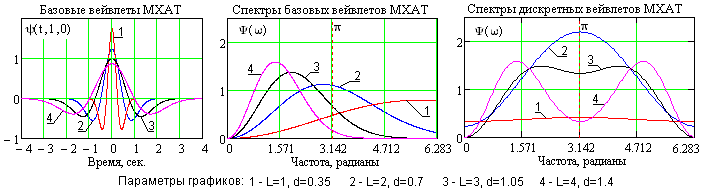
Рис. 22.1.8.

Для дискретного вейвлета МХАТ при L=2 и 3 форма спектра вейвлета в области высоких частот существенно искажена, что приведет к искажению строк вейвлет-спектра. Только начиная с L=4, при средней частоте вейвлета порядка /2 перекрытие с боковыми диапазонами становится не столь значимым.

Процесс преобразования начинается с задания интервалов и шага дискретизации по масштабу и сдвигу вейвлетов. Для наглядного сравнения с CWT повторим преобразование сигнала, приведенного на рис. 22.1.5, методом CDWT с заданием параметров дискретизации:

T = 200, B = T, b = 0..B, b =1, A = 60, a = 1..A, a = 1.

Дискретизации вейвлетной функции не требуется, она выполняется автоматически при вычислении вейвлетного спектра сигнала. Скалярное произведение дискретных функций требует задания в сигнале начальных (при одностороннем вейвлете) и конечных (при двустороннем вейвлете) условий. Особенностью CDWT является изменение интервала задания этих условий в прямой зависимости от масштаба вейвлета. Это означает, что продление произвольных сигналов должно производиться на длину LA, где А - максимальный заданный масштаб вейвлета. Для финитных сигналов выполнение этого требования (с заданием нулевых начальных и конечных условий) труда не представляет, как это и выполнено ниже. Формула преобразования:

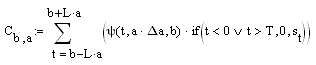(2.1.4)

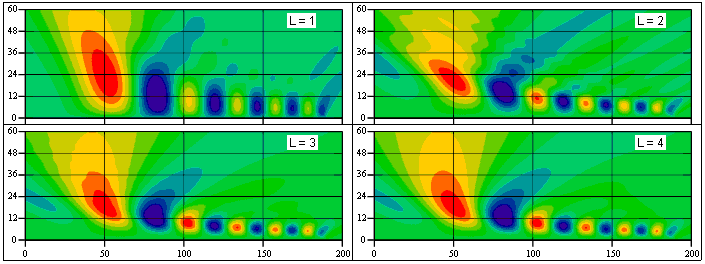
Рис. 22.1.9.

Рис. 22.1.10.

Примеры результатов преобразования приведены на рис. 22.1.9 при различных значениях параметра L для наглядного представления искажений, которые вносятся в дискретный спектр при неправильном выборе размеров базового вейвлета. При L=4 сравнением с рис. 22.1.5 можно убедиться в практической идентичности спектров CWT и CDWT.

На рис. 22.1.10 приведен пример преобразования ЛЧМ сигнала (рис. 22.1.5), на который наложен статистический шум, мощность которого в 3 раза больше мощности самого сигнала. Однако вид спектра хорошо фиксирует как общую картину спектра ЛЧМ сигнала, так и распределение во времени локальных неоднородностей.