13

Тема 17. Обработка изображений введение

Размах исследований в области цифровой обработки изображений стремительно нарастает. Это определяется тем, что обработка изображений — это обработка многомерных сигналов, а большинство сигналов в реальном мире является многомерными.

Изображение в математическом представлении - двумерный сигнал, несущий огромное количество информации. Цветное изображение размером 500 × 500 элементов - это массив в несколько сотен тысяч байтов. Обрабатывать такую информацию можно лишь рациональной организацией вычислений. Для конкретных задач обработки изображений можно применять эффективные способы обработки с учетом особенностей и ограничений этой конкретной задачи. Но если говорить об обработке изображений для решения широкого класса задач, то необходимо выделить набор стандартных операций, из которых можно строить алгоритмы для решения произвольных задач. К их числу относятся линейные преобразования, двумерная свертка и двумерное дискретное преобразование Фурье.

Но при обработке изображений широкое использование находят и нелинейные преобразования. Особенность изображений состоит в том, что отдельные элементы изображения находятся в определенной связи с соседними элементами. Поэтому большинство алгоритмов преобразования изображений носит локальный характер, т. е. обрабатывают изображения по группам элементов, располагающихся в окрестности вокруг данного. Линейные преобразования удовлетворяют свойству локальности и допускают построение алгоритмов, вычислительная сложность которых мало зависит от размеров охватываемой окрестности. Такие же свойства требуются и от нелинейных преобразований изображений. К классу таких преобразований относятся алгоритмы, которые называют алгоритмами ранговой фильтрации, основанными на вычислении локальных ранговых статистик изображений. При вычислении ранговых статистик и производных от них возможны упрощения, связанные с информационной избыточностью изображений. Наиболее известный алгоритм этого класса — алгоритм медианной фильтрации. Другими примерами ранговых алгоритмов могут служить алгоритмы экстремальной фильтрации, которые заменяют анализируемый элемент изображения максимумом или минимумом по окрестности. Еще одно свойство ранговых алгоритмов - локальная адаптация к характеристикам обрабатываемого изображения и потенциальные возможности их использования не только для сглаживания и очистки от шумов, но и для выделения признаков при автоматическом распознавании изображений.

При обработке изображений широко используются методы обработки одномерных сигналов, если возможно их обобщение на многомерные сигналы. При этом, приходится учитывать, что математические методы описания многомерных систем не отличаются завершённостью. Многомерные системы обладают большим числом степеней свободы, и их проектирование приобретает гибкость, не свойственную одномерным системам. В то же время, многомерные полиномы не разлагаются на простые множители, что усложняет анализ и синтез многомерных систем.

17.1. Основные понятия [1i]

Графическое представление изображений. Для представления графической информации на двумерной плоскости (экране монитора) применяются два подхода: растровый и векторный.

При векторном подходе графическая информация описывается как совокупность абстрактных геометрических объектов - прямые, отрезки, кривые, прямоугольники и т.п. Векторное описание предполагает априорные знания о структуре изображения.

Растровая графика оперирует с произвольными изображениями в виде растров. Растр (raster) - это описание изображения на плоскости путем разбиения (дискретизации) его на одинаковые элементы по регулярной сетке и присвоение каждому элементу своего цветового и любых других атрибутов. Самый простой растр – прямоугольный, самый экономичный по количеству отсчетов для передачи изображений - гексагональный. С математических позиций растр – это кусочно-постоянная аппроксимация на плоскости непрерывной функции изображения.

Элемент растра называют пикселем (pixel). Стандартная идентификация пикселей:

f(i, j) = (A(i, j),C(i, j)), (17.1.1)

где A(i, j)  R² - область пикселя, C(i, j)  C - атрибут пикселя (как правило, цвет). Чаще всего используются два вида атрибутов:

C(i, j) = I(i, j) - интенсивность (яркость) пикселя;

C(i, j) = {R(i, j), G(i, j), B(i, j)} - цветовые атрибуты в цветовой модели RGB.

В матричной форме:

M_ij = (A_ij , C_ij).

Рис. 17.1.1.

При дискретизации непрерывных изображений значения A_ij могут определяться двояко, либо как значения точек A_ij = (i, j), для которых определены атрибуты C_ij, либо как значения квадратов A_ij = (i, i+1) × (j, j+1) или любой другой формы, с определением C_ij по средним значениям в пределах этой формы (рис. 17.1.1).

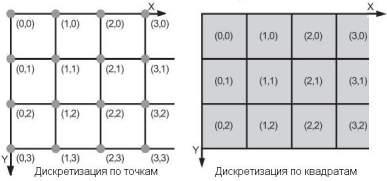
На практике, как правило, X и Y - ограниченные наборы неотрицательных целых чисел квадратного или прямоугольного растра с аспектовым отношением (aspect ratio) ширины к высоте растра, которое записывается в виде, например "4:3".

Представление цвета в машинной графике. Понятие цвета базируется на восприятии глазами человека электромагнитных волн в определенном диапазоне частот. Воспринимаемый нами дневной свет имеет длины волн λ от 400 нм (фиолетовый) до 700 нм (красный). Описанием светового потока может служить его спектральная функция I(λ). Свет называется монохроматическим, если его спектр имеет только одну определенную длину волны.

Рис. 17.1.2.

На сетчатке глаза находятся два типа рецепторов: палочки и колбочки. Спектральная чувствительность палочек (рис. 17.1.2) прямо пропорциональна яркости падающего света. Колбочки разделяются на три вида, каждый из которых имеет определенную чувствительность в ограниченных диапазонах с максимумами к красному, зеленому и синему цветам, и резко теряют свою чувствительность в темноте. Восприимчивость глаза к синему цвету значительно ниже, чем к двум другим. Важным свойством восприятия света человеком является линейность при сложении цветов с разными длинами волн.

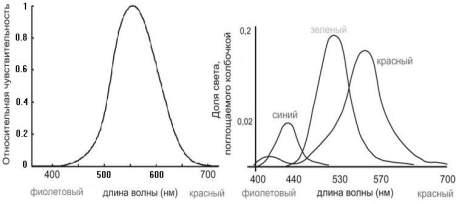
Цветовая модель RGB (Red, Green, Blue - красный, зеленый, голубой) в машинной графике в настоящее время является самой распространенной. В этой модели спектральная функция представляется как сумма кривых чувствительности для каждого типа колбочек с неотрицательными весовыми коэффициентами (с нормировкой от 0 до 1), которые так и обозначаются - R, G и B. Модель характеризуется свойством аддитивности для получения новых цветов. К примеру, кодировка спектральных функций:

- черного цвета: f_black = 0, (R,G,B) = (0,0,0);

- фиолетового цвета f_violet = f_red + f_blue, (R,G,B) = (1,0,1);

- белого цвета f_white = f_red + f_green + f_blue, (R,G,B) = (1,1,1).

Рис. 17.1.3.

Трехмерное пространство цветов модели RGB приведено на рис. 17.1.3. В силу особенностей восприятия света рецепторами не все цвета, видимые человеком, представимы в этой модели. Однако доля воспроизводимых цветов значительно больше, чем доля не представимых в этой модели.

Цветовая система CIE XYZ. Международный стандарт представления цвета CIE (CIE - Commission Internationale de l'Eclairage) был принят в 1931 году Международной комиссией по освещению, В нем определяются три базисные функции ρ_X(λ), ρ_Y(λ), ρ_Z(λ), зависящие от длины волны, линейные комбинации которых с неотрицательными коэффициентами (X, Y и Z) позволяют получить все видимые человеком цвета. Этими функциями учитывается относительное восприятие интенсивности света рецепторами глаза. В трехмерном пространстве цветовая система CIE образует конус в первом квадранте и применяется для высококачественного отображения цветных изображений.