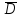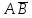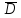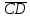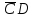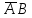1.2 Выбор и обоснование структурной схемы
В общем виде структурная схема будет выглядеть как блок, содержащий п входов и m выходов (рисунок1). Количество входов определяется количеством входных аргументов (операнд), а количество выходов зависит от количества переключательных функций.
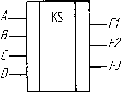
Структурная схема для узла, функционирующего в соответствии с уравнениями задания:
F1(A,B,C,D) = Σ (0,1,2,3,5,9,10,13)
F2(A,B,C,D) = Σ (1,5,9,10,12,13,14)
F3(A,B,C,D) = Σ (1,5,9,12,13,14)
должна содержать четыре входа для операндов А, В, С, D и три выхода для функций F1, F2 и F3 (рисунок 2).
1.3 Логический расчет комбинационной схемы
Целью данного раздела является получение МДНФ заданных функций для дальнейшего построения схемы с минимальным количеством элементов.
Характер функционирования комбинационной схемы задан следующими исходными функциями:
F1(A,B,C,D) = Σ (0,1,2,3,5,9,10,13)
F2(A,B,C,D) = Σ (1,5,9,10,12,13,14)
F3(A,B,C,D) = Σ (1,5,9,12,13,14)
Минимизируем функции с помощью карт Карно, заполняя их в соответствии с рисунком 3.
|
|
CD |
C |
|
|
|
AB |
15 |
14 |
12 |
13 |
|
|
11 |
10 |
8 |
9 |
|
|
3 |
2 |
0 |
1 |
|
|
7 |
6 |
4 |
5 |
Рисунок 3 - Карта Карно
Для функции F1:
|
|
CD |
C |
|
|
|
AB |
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
1 |
1 |
1 |
1 |
|
|
|
|
|
1 |
После сокращений: F1ДНФ = CD + АВ + BCD
|
|
CD |
CD |
CD |
CD |
|
АВ |
|
n |
Cl \ |
I |
|
АВ |
|
и |
|
i ! i 1 ! 1 1 |
|
АВ |
|
|
|
H |
|
АВ |
|
|
|
1 I \ 1 j ' |
После сокращений: БгднФ - CD + ABC + ACD Для функции F3:
|
|
CD |
CD |
CD |
CD |
|
|
|
|
' V |
N |
|
AB |
|
1 |
1 ) |
' 1 \ ■ \ i |
|
AB |
|
|
|
1 ! i |
|
AB |
|
|
|
> I |
|
AB |
|
|
|
■ 1 1J |
После сокращений: Рзднф = CD + ABD Для функции Fj F2:
|
|
CD |
CD |
CD |
CD |
|
|
AB |
|
|
|
(fiN |
|
|
AB |
|
11 |
|
j.l |
|
|
AB |
|
|
|
11 |
|
|
AB |
|
|
|
|
|
После сокращений: Р^гднФ = CD + ABCD
После сокращений: РгРзднФ = CD + ABD Для функции F1F2F3:
|
|
CD |
CD |
CD |
CD |
|
|
АВ |
|
|
|
fUl |
|
|
АВ |
|
|
|
j 111 |
|
|
АВ |
|
|
|
111 |
|
|
АВ |
|
|
|
1Ш, |
|
После
сокращений: Р^Рзднф
= CD
Минимизируем полученные функции, используя метод Квайна.
Составляем импликантную матрицу (таблица 1), число строк которой равно числу импликант в выражениях, а в столбцах записываем все конституэнты единицы, входящие в исходные выражения переключательных функций.
Таблица 1 - Импликантная матрица
|
|
ABCD |
ABCD |
ABCD |
ABCD |
ABCD |
ABCD |
ABCD |
ABCD |
ABCD |
ABCD |
|||||||||||||||||||
|
|
Fi |
Fi |
f2 |
F3 |
Fi |
Fi |
Fi |
f2 |
F3 |
Fi |
f2 |
F3 |
Fi |
f2 |
f2 |
F3 |
Fi |
f2 |
F3 |
f2 |
F3 |
||||||||
|
CD Fi F2F3 |
|
• |
• |
• |
|
|
• |
• |
• |
• |
• |
• |
|
|
|
|
• |
• |
• |
|
|
||||||||
|
АВ F, |
• |
• |
|
|
• |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
BCD Fi |
|
|
|
|
• |
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
||||||||
|
ACD f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
• |
|
||||||||
|
ABC Fa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
• |
|
|
|
||||||||
|
ABD F2, F3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
• |
|
|
|
• |
• |
||||||||
|
ABCD Fi, F2 |
|
|
|
|
|
|
|
|
|
|
|
|
• |
• |
|
|
|
|
|
|
|
||||||||
Окончательно получаем:
Fi = CD + АВ +ABCD _
F2 = CD + ABC + ABCD F3 = CD + ABD
Для того, чтобы реализовать функцию на элементах «ИЛИ-HE» необходимо привести ее к соответствующему базису:
Fi_ = CD + АВ + ABCD = CD * АВ * ABCD = (С + D) * (А + В) * (А + В + С + D) =(С + D) + (А + В) + (A + B + C + D)
F2 = CD + ABC + ABCD = £Р * АВЁ * ABCD = (C + D)*(A+B + C)*(A + B + C + dT=(cT5)+ (A +B +С) + (A + B + C + D)
F3 = CD + ABS = CD * ABD = (C + D) * (A + В + D) = (C + D) + (A + В + D)
Схема приведена в приложении A-l.