
- •Вопросы:
- •Лекция №1.
- •Лекция№2 Классификация методов контроля и испытаний
- •Испытания
- •Лекция №3 Измерительные приборы Основные понятия и определения
- •Классификация измерительных приборов:
- •Сущность измерения Уравнение измерения.
- •Аналоговый и цифровой методы измерения.
- •Метод отклонения. Компенсационный (нулевой) метод.
- •Погрешности измерений и причины погрешностей
- •6 Лекция Погрешности, связанные с обработкой измеренных значений.
- •Характеристики погрешностей измерительных приборов.
- •Линейная регрессия.
- •Доверительные границы для коэффициента регрессии.
- •Линейная корреляция.
- •Измерение как процесс передачи сигналов
- •Измерительные сигналы и их математическое описание
- •Временные характеристики детерминированных измерительных сигналов
- •Временные характеристики стохастических сигналов
- •Корреляционная функция
Характеристики погрешностей измерительных приборов.
Порог реагирования.
Если входная величина измерительного устройства медленно и непрерывно увеличивается от нуля, то выходная величина начинает изменяться только при определенных значениях входной величины. Абсолютная величина этого значения называется порог реагирования (нечувствительности). Чтобы исключить неопределенность, связанную с обнаружением факта начала изменения показания, предусматривают определённое малое изменение показания ΔXa.
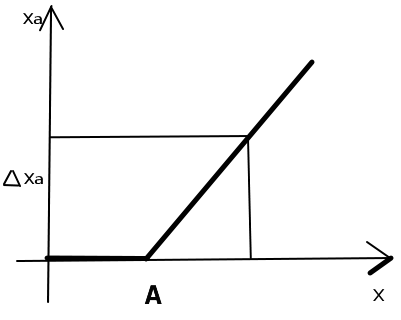
Статическая характеристика с нечувствительностью в нулевой точке. А-пороге реагирования для ΔXa.
Для счетных (интегрирующих) измерительных приборов устанавливается порог реагирования, т.е нагрузка, при которой прибор начинает счет.
Вариация показаний. Гистерезис.
Вариацией показаний называется разность показаний, получаемая при одном и том же значении измеряемой величины при медленном, непрерывном или шаговой подходе к метке шкалы в первый раз-с меньшего, в другой-с большего значения. Причины вариации могут быть различны: при наличии люфта в механическом передающем элементе характеристика имеет следующий вид:

Для люфта характерно постоянное значение Ха. Аналогичная характеристика будет иметь место при сухом трении. Однако в этом случае вариация может зависеть от измеряемого значения.
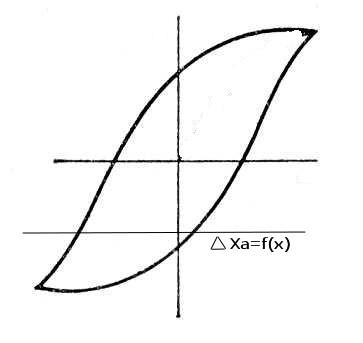
Сухое трение

В случае гистерезиса.
Гистерезис связан с феррорезонансными с явлениями в электрических цепях. При этом вариация зависит от того, что было раньше (до проведения измерений).
Аналогичная характеристика может иметь место и при механическом гистерезисе. Например, внутреннее трение в материале пружины может привести к таким явлениям (остаточные деформации) после снятия нагрузки. Остающаяся разность зависит от величины нагрузки.
Упругое последействие.
Если какой-либо подвижный упругий элемент находится в течение длительного времени в отклоненном состоянии, то он больше не возвращается в своей исходное состояние покоя. Остающаяся разность зависит как от размера отклонения, так и от его длительности. С течением времени упругое последействия исчезает.
Разрешающая способность.
Употребляется в разных значениях. Если измеряемая величина начинает медленно и непрерывно увеличиваться от любого ненулевого значения, то в общем случае изменение показания констатируется не сразу. При этом под разрешающей способностью понимается значение входной величины, необходимое для начала изменения показания.
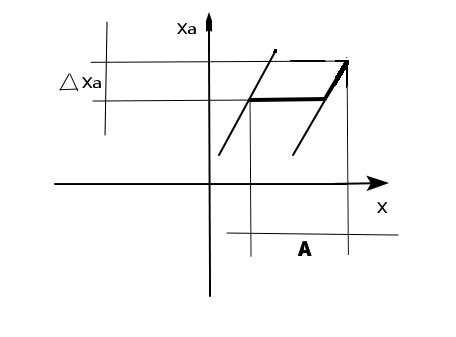
При отсутствии гистерезиса, определенная таким образов разрешающая способность соответствует обратной величине чувствительности.
Если показания изменяются дискретно, то часто разрешающей способностью называют шаг дискретности показания. В цифровых приборах Разрешающая способность определяется как значение младшего разряда цифрового счета.
Стабильность нуля.
Смещение нуля является причиной аддитивной помехи. Стабильность нуля, в частности электрического устройства, часто характеризуют отклонением смещения нуля к значению помехи, его вызвавшему. (мВ/К). Временную нестабильность точки нуля определяют значением максимального дрейфа нуля за определенное время. При этом должны быть оговорены условия применения.
Недостоверность измерения.
При измерении могут иметь место как систематические, так и случайные погрешности. Если систематическую погрешность скорректировать, то остается случайная. В этом случае результат измерения (в определенной мере) является недостоверным. Однако при статистическом рассмотрении погрешности можно указать, с какой вероятностью погрешность останется ниже определенного значения, т.е. недостоверность измерения-это размер погрешности, который не будет превышен с определенной степенью вероятности. Иногда в недостоверность включают и неучтенные систематические погрешности. Указание погрешности для характеристики недостоверности измерения вовсе не означает, что на самом деле погрешность никогда не превзойдет указанного значения. Это соответствует действительности лишь с определенной вероятностью. В отличие от этого, предел допускаемой погрешности указывает размер погрешности, который никогда не может быть превышен измерительным прибором.
Линейность поля допуска.
Если номинальная зависимость между измеряемой величиной и показаниями принимается линейной, то указание погрешности нелинейности служит для описания отклонения от номинальной характеристики.
Чаще всего указываются максимальные отклонения от требуемой прямой, выраженные в процентах от диапазона показаний.
Рассмотрим два наиболее употребительных понятия линейности:
-
Основано на том, что прямую проводят через номинальное значение шкалы линейности.
 (
в процентах от диапазона показаний)
(
в процентах от диапазона показаний)
Однако часто, прямую проводят так, чтобы сумма квадратов погрешностей была минимальной.
-
В отличие от 1 варианта, максимальное отклонение, указанное в значении недостоверности измерения.

1 – определение понятия линейности подходит для характеристики приборов, с преобладающими систематическими погрешностями;
2 – подходит, для характеристики приборов, с преобладающими случайными погрешностями.
С понятием линейности тесно связано установление поля допуска, при этом необходимо указывать в каком из двух значений, предельно допустимая погрешность или недостоверность измерений, следует его понимать.
Если исходить из указания аддитивности погрешности, независящей от измеренного значения, то поле допуска получается:
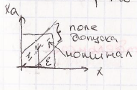
Погрешность накладывается и не зависит от измеряемой величины. ɛ - величина относительной погрешности. Если погрешность мультипликативная, т. е. зависит от измеренного значения, тогда:
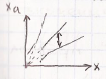 В
верхней части ɛ=Е/х=const,
в нижней, при х→∞, теоретически
погрешность →0. Поэтому, вблизи нуля,
мультипликативное поле допуска заменяется
постоянной абсолютной погрешностью.
В
верхней части ɛ=Е/х=const,
в нижней, при х→∞, теоретически
погрешность →0. Поэтому, вблизи нуля,
мультипликативное поле допуска заменяется
постоянной абсолютной погрешностью.
Статические погрешности измерения.
Погрешности, возникающие при определении постоянного во времени измеренного значения, называются статическими, при этом предполагают, что измерительный прибор и измеряемая величина находятся в установившемся положении.
ха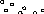
Ea μ
х
Ес – систематическая погрешность; Еа – отклонения.
Ес = μ-х, где μ – среднее арифметическое (математическое ожидание), х – измеренное значение.
 ,
,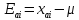
Случайная погрешность отдельного измерения.
Колебания случайной погрешности, кажущиеся беспорядочными в статическом смысле, подчиняются определенными законам.
Если показания измерительного прибора разбить на интервалы определенной ширины ∆х и вычислить относительную частоту показаний в отдельных интервалах при повторных измерениях, то можно получить гистограмму:

Распределение вероятности является предельным, так как, если смещать выборки с распределением, и снова обработать, то получим нормальный закон.
Параметры:
μ - математическое ожидание (выборка – оценка математическое ожидание, вся партия- истинное математическое ожидание μ);
σ – среднее квадратическое отклонение (имеет размерность, показывает расплывчатость закона, в статистике используется относительное значение σ).
При известном σ можно вычислить, что случайная погрешность Ес (для отдельного измерения) будет меньше заданного граничного значения с. Эта вероятность называется доверительной вероятностью или статической надежностью.
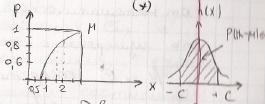
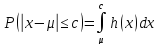
На практике, обычно, значение доверительной вероятности принимают 95-99%.
При известном значении с, с помощью такого графика можно, на основании измерения, показать верхнюю и нижнюю границу математического ожидания.


Математическое ожидание с доверительной вероятностью Р (в процентах) лежит внутри этих границ. Интервал между этими границами называется доверительным интервалом математического ожидания.
Часто случайную погрешность, определяемую доверительной вероятностью, называют также недостоверностью измерения. Эта погрешность статистически описывает только отклонения от математического ожидания, а не правильность измерения.
μ и σ теоретически, принадлежат генеральной совокупности; в каждой реальной выборке – величины оценки параметров. σ2 – дисперсия (второй момент плотности распределения вероятности).
В качестве оценки σ используется рассеяние:
 (теряется
1 степень свободы), S2
– состоятельная оценка. При n→∞,
S→σ.
(теряется
1 степень свободы), S2
– состоятельная оценка. При n→∞,
S→σ.
Случайная погрешность среднего значения.
Чтобы избежать недостоверности случайной погрешности единичного замера, можно усреднить несколько измерений. Но полученное среднее значение является только случайной величиной, так как n – является выборкой (конечным числом), среднее квадратическое отклонение у него меньше, чем у единичного измерения.
Между
средним квадратическим отклонением
среднего значения
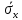 и средним квадратическим отклонением
измерения
и средним квадратическим отклонением
измерения
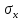 имеется соотношение:
имеется соотношение:
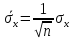
Усреднение
позволяет уменьшить доверительную
границу погрешности, при заданной
доверительной вероятности пропорционально
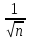 .
.
Систематическая погрешность градуировки.
Систематическая
погрешность Ес=μ-х,
реально μ→ ,
полученную при многократных измерениях.
,
полученную при многократных измерениях.
Ес≈х- .
.
В связи с тем, что систематическая погрешность является воспроизводимой, ее можно определить при поверке прибора и учесть при проведении измерений.
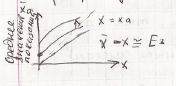
Градуировочная кривая с систематической погрешностью, зависящая от размера измеренного значения.
Так как точно может быть определено только среднее значение, а не математическое ожидание, то градуировочная кривая имеет смысл лишь в том случае, если результат случайной погрешности определяемого среднего значения при градуировке существенно меньше, чем систематическая погрешность. Поэтому градуировка по одиночному измерению без априорного значения случайной погрешности или доверительного интервала лишена смысла.
Если используемые при градуировке меры или приборы сравнения имеют значительные рассеяния, то результирующая погрешность должна определяться на основе законов распространенных погрешностей.
Распространение погрешности
Если результат измерения определяется на основе математической обработки отдельных измеренных значений, то погрешность вводится и в этот результат, поэтому говорят о распространении погрешности. Различным структурам систематических и случайных погрешностей соответствуют разные законы распространения погрешностей.
Систематические погрешности
Результат измерения y определяется по m различным измеренным значениям xi. В статике эта связь описывается уравнением:

При малых отклонениях результирующее отклонение можно рассчитать, используя первые члены ряда Тейлора:
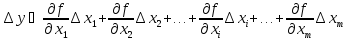
Если
под малыми отклонениями
 понимать систематическую погрешность
понимать систематическую погрешность
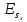 ,
то это уравнение можно переписать:
,
то это уравнение можно переписать:

Следует
отметить, что систематическая погрешность
может иметь знак «+» или «−» вследствие
чего возникает возможность ее компенсации.
Особое значение, предъявленное к
систематической погрешности, имеет
частная производная
 .
Эти весовые (влияющие) коэффициенты
показывают, каким весом отдельные
систематические погрешности участвуют
в образовании систематической погрешности
результата измерения.
.
Эти весовые (влияющие) коэффициенты
показывают, каким весом отдельные
систематические погрешности участвуют
в образовании систематической погрешности
результата измерения.
Случайные погрешности
Случайная погрешность, рассматриваемая как единичное явление, по своей природе не может быть предсказано заранее, однако можно высказать суждение о ее статистических свойствах.
При
нормальном распределении погрешности
СКО
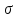 является мерой, характеризующей плотность
распределения погрешности, поэтому
вопрос о распространении погрешности
сводится к способу распространения
статистической характеристики
является мерой, характеризующей плотность
распределения погрешности, поэтому
вопрос о распространении погрешности
сводится к способу распространения
статистической характеристики
 или доверительных границ.
или доверительных границ.
Требуется
определить СКО
 При известной функции (*), СКО
При известной функции (*), СКО
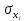 для величин
для величин
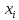 .
.
Если
отдельные влияющие величины взаимно
независимы и для величин выполняется
условие
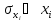 ,
то
,
то
 можно определить:
можно определить:
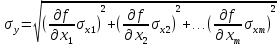
Если
вместе с СКО
 подставить их оценки рассеивания
подставить их оценки рассеивания
 ,
то получим соотношение для определения
рассеивания результата
,
то получим соотношение для определения
рассеивания результата
 ( не строгое):
( не строгое):
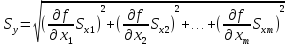
Используя
 в качестве оценки
в качестве оценки
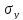 можно определить доверительные границы
погрешности при выбранной доверительной
вероятности.
можно определить доверительные границы
погрешности при выбранной доверительной
вероятности.
Для увеличения точности расчета результата измерения можно использовать среднее значение влияющих величин:
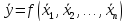
Если для усреднения каждой из m величин используется n значений, то СКО или рассеивание будет уменьшаться

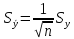
Если рассеивание S(xi) влияющих величин заранее не известно, то можно определить его одновременно с усреднением xi, используя те же n значений.
В этом случае приведенное соотношение и график не могут быть использованы. Доверительные границы погрешности среднего значения результата измерения определяют по формуле:
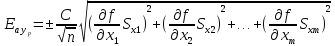
Величину
С определяют по графикам для выбранной
доверительной вероятности Po
и числу степеней свободы
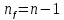
Предел погрешности.
Его применяют для задания максимального гарантированного значения погрешности. Этот предел содержит как оценочную систематическую, так и случайную погрешность. Пределы погрешности отдельно измеренных значений могут иметь положительные, отрицательные или неопределённые знаки. При неопределённых знаках, предел погрешности результата измерений определяется суммированием абсолютных значений пределов погрешности отдельных измеренных значений.

 -погрешность
-погрешность
Если знаки пределов погрешности измеренных значений известны, то положительные и отрицательные пределы погрешности результата измерений вычисляются по отдельности.
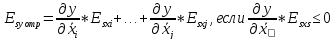

Методы обработки, связанные со статистическими погрешностями.
Проверка гипотезы нормальности распределения.
Рассмотрим два варианта проверки гипотезы нормальности закона распределения генеральной совокупности, из которых взята данная выборка. Наиболее простой вариант, состоящий в сопоставлении измеренного распределения с нормальным, основан на исследовании диаграммы накопленной частоты. Числовые пометки на оси ординат нанесены таким образом, что нормальному распределению соответствует прямая линия. Накопленную частоту измеренных значений наносят на диаграмму, изображенную на рисунке. После этого проводят прямую таким образом, чтобы отклонение от точек было бы минимальным. Суждение о том, насколько хорошо распределение соответствует нормальному, высказывается после рассмотрения следующих вопросов:
-
В какой мере точки удалены от прямой.
-
Насколько рассчитанное среднее значение
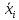 выборки
отклоняется от определенного с помощью
прямой математического ожидания
нормального распределения µ. Величина
µ считывается с диаграмм при накопленной
частоте 50 %.
выборки
отклоняется от определенного с помощью
прямой математического ожидания
нормального распределения µ. Величина
µ считывается с диаграмм при накопленной
частоте 50 %.
Замечание: значение 100% накопленной частоты, которая достигается в выборке, на диаграмму не наносят. Это связано с тем, что нормальное распределение допускает бесконечно большое отклонение от ожидаемого значения. Нормальное распределение представляет собой лишь приближенную модель действительное распределение. Однако бесконечно большие отклонения не встречаются. Вероятность бесконечно больших отклонений мала, поэтому внимание надо уделять отклонениям, находящимся в области среднего значения. Поэтому не следует обращать внимание на отклонение накопленной прямой меньше 10% и больше 90%.

Диаграмма накопленной частоты для проверки нормальности распределения. Рассмотренная процедура дает только качественную ,грубую оценку. Тем не менее, она пригодна для обнаружения отклонения от нормального распределения. Качественная оценка определяется с помощью хи-квадрат распределения.
-
Определяем из выборки оценки.
 и
и
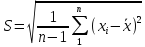
-
Разбиваем измеренные значения на K интервалов K>4,таким образом, чтобы в каждом интервале было >5 значений.
-
Определяют число измеренных значений в каждом интервале nsi.
-
Для нормального распределения с
 и
и
 ,
находим вероятность pi
попадания измеренных значений в i-ый
интервал. По этой вероятности определяют
число измеренных значений noi,
которые должны были попасть в этот
интервал при нормальном распределении.
,
находим вероятность pi
попадания измеренных значений в i-ый
интервал. По этой вероятности определяют
число измеренных значений noi,
которые должны были попасть в этот
интервал при нормальном распределении.
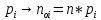
-
Вычисляется выражение

И используя рисунок решают, имеет место нормальное распределение или нет.
К-число интервалов, используемых при проверке.
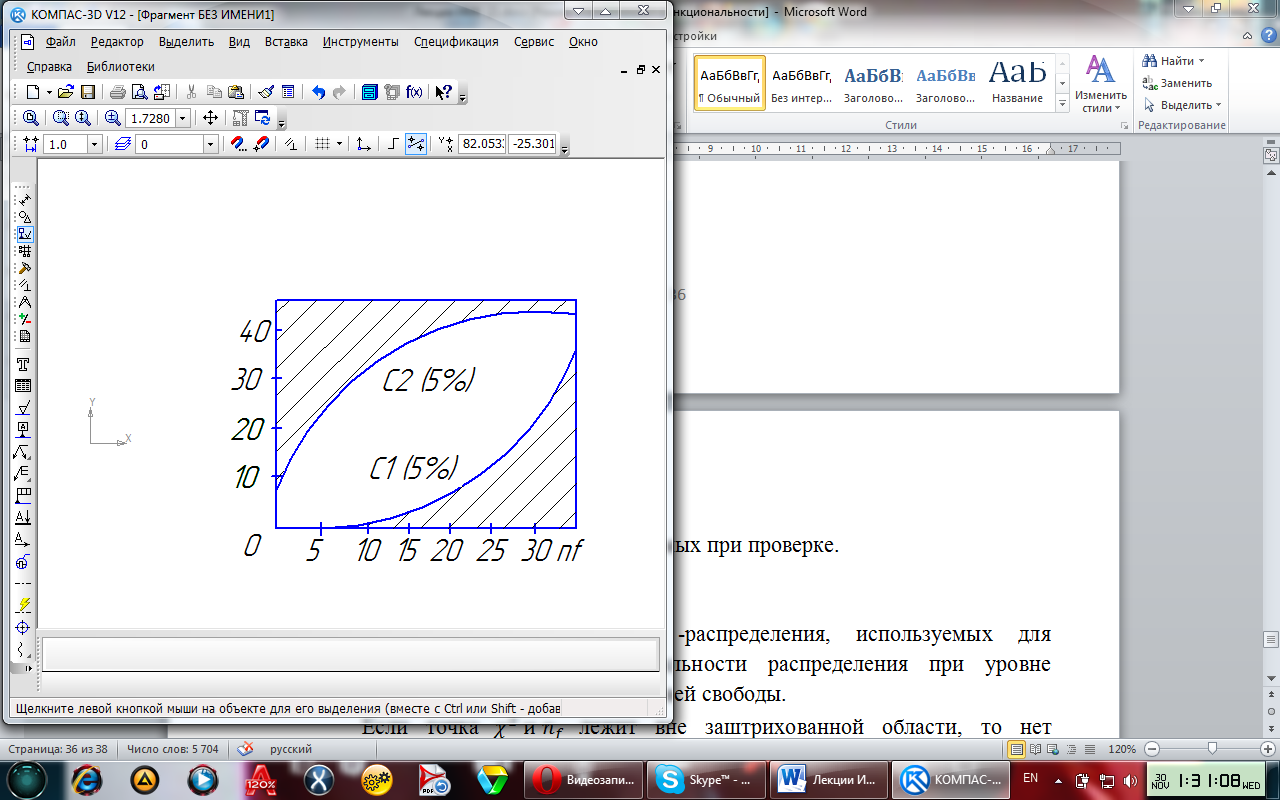

Доверительные
границы
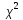 -распределения,
используемых для проверки гипотезы о
нормальности распределения при уровне
значимости 5%.
-распределения,
используемых для проверки гипотезы о
нормальности распределения при уровне
значимости 5%.
 -число
степеней свободы.
-число
степеней свободы.
Если
точка
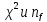 лежит вне заштрихованной области, то
нет оснований сомневаться в том, что
генеральная совокупность, откуда
произведена выборка, имеет предположительно
нормальное распределение. Однако это
не означает, что речь идет о каждом
случае нормального распределения. Можно
только утверждать, что если нормальное
распределение действительно имеет
место, то выражение
лежит вне заштрихованной области, то
нет оснований сомневаться в том, что
генеральная совокупность, откуда
произведена выборка, имеет предположительно
нормальное распределение. Однако это
не означает, что речь идет о каждом
случае нормального распределения. Можно
только утверждать, что если нормальное
распределение действительно имеет
место, то выражение
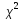 в среднем только в 5% всех случаев лежит
в верхней и в 5% всех случаях- в нижней
заштрихованных областей. Поэтому, если
в среднем только в 5% всех случаев лежит
в верхней и в 5% всех случаях- в нижней
заштрихованных областей. Поэтому, если
 попадает в эти области, то гипотеза о
нормальности распределения отвергается.
попадает в эти области, то гипотеза о
нормальности распределения отвергается.
Грубые погрешности измерения
Если большое число измеренных значений привлекаем для дальнейшей обработки, то каждый раз возникает сомнение, не входят ли грубые ошибки. Ответ получают следующим образом:
-
Предполагают, что различие в ряде измерений обусловлены случайными погрешностями (нормальное распределение).
-
По измеренным значениям определяют характеристики распределения. Для нормального распределения такими характеристиками являются среднее значение
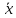 и рассеяние S.
и рассеяние S.
-
Выбирают доверительную вероятность 95%.
-
Для предполагаемого нормального распределения с
 и
и
 ,
можно по графикам определить доверительный
интервал при выбранной доверительной
вероятности. Это означает, что
доверительный интервал +1,96
,
можно по графикам определить доверительный
интервал при выбранной доверительной
вероятности. Это означает, что
доверительный интервал +1,96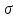 ,
т.е. только в 2,5% всех случаев попадают
значения x>
,
т.е. только в 2,5% всех случаев попадают
значения x>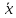 +1,96
+1,96 и в 2,5% случаев x<
и в 2,5% случаев x< 1,96
1,96 .
Для измеренных значений, лежащих вне
доверительного интервала, отвергаем
гипотезу об их принадлежности к
генеральной совокупности и считаем,
что эти значения являются грубой
погрешностью.
.
Для измеренных значений, лежащих вне
доверительного интервала, отвергаем
гипотезу об их принадлежности к
генеральной совокупности и считаем,
что эти значения являются грубой
погрешностью. -
После исключения грубой погрешности рассчитывает исправленные оценки
 и
S.
и
S.
