Министерство образования Российской Федерации

Ивановский государственный химико-технологический университет

№ 866

Информатика

Часть 3

Основы вычислительной математики

Методические указания и контрольные работы для студентов заочного обучения

Составители: С.П. Бобков,

В.А. Бобкова

Иваново 2003

Составители: С.П. Бобков, В.А. Бобкова

УДК 613.19

Информатика. Часть 3. Основы вычислительной математики: Методические указания и контрольные работы для студентов заочного обучения / Сост.: С. П. Бобков, В. А. Бобкова; Иван. гос. хим.-технол. ун-т. – Иваново, 2003. 32 с.

Методические указания являются третьей частью серии методических указаний по курсу «Информатика» для студентов заочного обучения. Рассмотрены следующие темы: приближенное решение нелинейных уравнений; решение систем линейных алгебраических уравнений; решение обыкновенных дифференциальных уравнений; аппроксимация функций с помощью метода наименьших квадратов; линейное программирование. Приведены примеры и задания для выполнения лабораторных работ.

Предназначены для самостоятельной работы студентов заочной формы обучения всех специальностей.

Табл. 9. Ил. 17. Библиогр.: 7 назв.

Рецензент доктор технических наук, профессор А. Н. Лабутин (Ивановский государственный химико-технологический университет)

Введение

Основными целями лабораторного практикума по курсу "Информатика. Основы вычислительной математики" являются:

- закрепление знаний по теоретическим основам использования методов вычислительной математики для анализа математических моделей технических и экономических объектов;

- получение практических навыков работы на компьютерах, отладки и тестирования программ.

Методические указания являются третьей частью серии методических указаний по курсу «Информатика» для студентов заочного обучения. Они содержат описание ряда численных методов, примеры решения конкретных задач и индивидуальные задания для самостоятельных лабораторных работ. В указаниях рассмотрены следующие темы: приближенное решение нелинейных уравнений; решение систем линейных алгебраических уравнений; решение обыкновенных дифференциальных уравнений; аппроксимация функций с помощью метода наименьших квадратов; линейное программирование.

Для реализации численных методов в процессе решения поставленных задач предполагается использование среды программирования Turbo Pascal или процессора электронных таблиц MS Excel.

Требования к оформлению лабораторных работ

Лабораторные работы оформляются в тетради в виде отчета, который должен содержать:

1. Номер варианта

2. Название лабораторной работы.

3. Задание.

4. Расчетная часть:

   1. Краткое теоретическое описание метода.

   2. Ручной расчет для двух-трёх шагов.

   3. Текст программы или описание хода решения задачи с использованием MS Excel.

   4. Введенные исходные данные и результаты расчетов.

5. Вывод.

1. Приближенное решение нелинейных уравнений

Пусть дано уравнение с одним неизвестным

, (1.1)

где - заданная алгебраическая или трансцендентная функция.

Решить уравнение - значит найти все его корни, то есть те значения , которые обращают уравнение в тождество, или доказать, что корней нет.

В общем случае не существует формул, по которым определяются точные значения корней уравнения (1.1). Для отыскания корней используют приближенные методы, при этом корни находятся с некоторой заданной точностью. Это означает, что если - точное значение корня уравнения, а - его приближенное значение с точностью , то . Если корень найден с точностью , то принято писать .

Будем предполагать, что уравнение (1.1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность, не содержащая других корней этого уравнения.

Приближенное решение уравнения состоит из двух этапов:

1. Отделение корней, то есть нахождение интервалов из области определения функции , в каждом из которых содержится только один корень уравнения (1).

2. Уточнение корней до заданной точности.

Отделение корней можно проводить графически и аналитически.

Для того, чтобы графически отделить корни уравнения (1.1), строят график функции . Абсциссы точек его пересечения с осью Ox есть действительные корни уравнения (рис. 1). Практически бывает удобнее заменить уравнение (1.1) равносильным ему уравнением

, (1.2)

где и - более простые функции, чем . Абсциссы точек пересечения графиков функций и дают корни уравнения (1.2), а значит и исходного уравнения (1.1) (рис.2).

Аналитическое отделение корней основано на следующей теореме: если непрерывная на отрезке функция принимает на концах отрезка значения разных знаков, т.е. , то внутри этого отрезка находится хотя бы один корень уравнения ; если при этом производная со-

Функция называется алгебраической, если для получения её значения нужно выполнить арифметические операции и возведение в степень с рациональным показателем. Примеры трансцендентных функций - показательная, логарифмическая, тригонометрические, обратные тригонометрические.

храняет знак внутри отрезка , то корень является единственным.

Рис. 1. Рис. 2.

Уточнение корней заключается в сужении интервала изоляции корня и выполняется одним из специальных методов. Рассмотрим самый простой из них - метод половинного деления.

П

рень. Если , то в качестве нового отрезка изоляции корня выбираем ту половину или , на концах которой принимает значения разных знаков. Другими словами, если , то корень принадлежит отрезку , если - отрезку . Полученный отрезок снова делим пополам, находим ,

усть корень отделён и принадлежит отрезку . Находим середину отрезка по формуле (рис.3). Если , то с - искомый ко-

Рис. 3.

вычисляем , выбираем отрезок и т.д. Длина каждого нового отрезка вдвое меньше длины предыдущего, то есть за шагов отрезок сократится в раз. Как только будет выполнено , то в качестве приближенного значения корня, вычисленного с точностью , можно взять .

Пример. Пусть требуется решить уравнение с точностью =0,0001. Отделим корень графически. Для этого преобразуем урав-

(рис. 4). Из рисунка видно, что абсцисса точки пересечения этих графиков принадлежит отрезку .

Подтвердим аналитически правильность нахождения отрезка изоляции корня. Для отрезка имеем:

;

. Следовательно, корень отделён правильно.

нение к виду и построим графики функций и

Рис. 4.

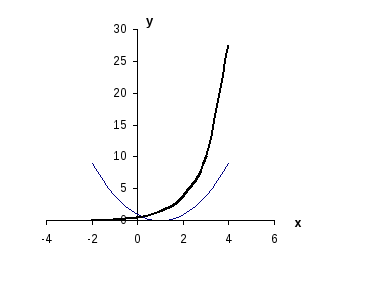
Уточнение корня выполним методом половинного деления.

Первый шаг.

Корень принадлежит отрезку

Второй шаг.

Корень принадлежит отрезку

Третий шаг.

Корень принадлежит отрезку

Сведём результаты вычислений в таблицу.

Таблица 1.

a	b		c	f(a)	f(c)
0	1	1	0.5	0.5	-0.57436	<0
0	0.5	0.5	0.25	0.5	-0.07951	<0
0	0.25	0.25	0.125	0.5	0.19905	>0
0.125	0.25	0.125

Дальнейшие вычисления проведём с помощью программы.

program equation; {Решение уравнения методом половинного деления}

uses crt;

var

a,b: real; { Концы отрезка }

c: real; { Середина отрезка }

e: real; { Точность }

function f(x: real): real;

begin

f: = sqr(x-1) - 0.5*exp(x); { Функция f(x) }

end;

begin

writeln (' Введите концы отрезка : ');

write (' a = '); readln ( a );

write (' b = '); readln( b );

write (' Введите точность e = '); readln ( e );

writeln(' Результат : ');

while abs ( b - a ) > 2*e do

begin

c: = ( a + b ) / 2;

if f( c ) = 0 then

begin

writeln( ' c = ' , c : 8 : 6 , ' f( c ) = ' , f( c ) : 8 : 6 );

readln ;

exit ;

end;

if f(a) * f(c) < 0 then b: = c else a: = c;

end;

c: = ( a + b ) / 2;

writeln( ' c = ' , c : 8 : 6, 'f( c ) = ' , f( c ) : 8 : 6 );

readln;

end.

Были введены следующие значения: a = 0, b = 1, e = 0.0001.Получены результаты: с = 0.213287; f ( c ) = 0.000047.

Ответ: корень уравнения равен 0,21330,0001.

Задания. Найти корень уравнения (если корней несколько, взять наименьший положительный) с точностью 0,0001.

Таблица 2.

№ варианта	Уравнение	№ варианта	Уравнение
0		5
1		6
2		7
3		8
4		9