4. Решение обыкновенных дифференциальных уравнений

Решение дифференциальных уравнений является одной из важнейших математических задач, поскольку большинство исследований в механике, физике, биологии предполагают анализ процессов, описываемых дифференциальными уравнениями.

Существует несколько существенно различных классов дифференциальных уравнений. В данном пособии мы остановимся только на обыкновенных дифференциальных уравнениях (ОДУ) первого порядка. Такие уравнения содержат только первую производную от искомой функции от одной независимой переменной. В общем виде ОДУ первого порядка можно записать так:

F(x, y, y) = 0,

(4.1)

где у – функция независимого аргумента х; y - первая производная этой функции.

Для численного решения следует переписать уравнение (4.1) в виде (4.2), разрешив его относительно производной:

y = f(x, y).

(4.2)

Из курса высшей математики известно, что общее решение уравнений (4.1), (4.2) содержит произвольную постоянную С. Частное решение получается из общего, если произвольной постоянной придать конкретное значение. Для этого необходимо задать дополнительное условие, которое обычно представляет собой значение функции при некотором начальном значении независимой переменной:

(4.3)

Большинство методов численного решения ОДУ основано на следующем приёме. Область непрерывного изменения аргумента заменяется дискретным множеством точек, называемых узлами. Узлы составляют разностную сетку. Искомая функция непрерывного аргумента приближенно заменяется функцией дискретного аргумента на заданном множестве узлов сетки. В этом случае исходное уравнение (4.2) заменяется разностным уравнением (4.4), где производная представлена отношением конечных разностей:

(4.4)

Здесь y_i – значение искомой функции в i-м узле сетки, x_i - значение независимой переменной в этом узле, h – шаг сетки.

Рассмотрим простейший метод решения ОДУ, называемый методом Эйлера. Расчетная формула метода непосредственно вытекает из (4.4):

(4.5)

где i = 0, 1, 2, … . При этом на первом шаге (i = 0) используется начальное условие (4.3).

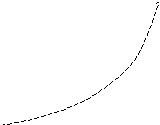
Рассмотрим геометрическую интерпретацию метода Эйлера (рис. 9). Начальная точка А(х₀, у₀) находится на интегральной кривой 1, которая является точным решением дифференциального уравнения. Ордината у₁ точки В есть сумма у₀ +  у₀, где  у₀ = h  tg . Но поскольку tg  есть тангенс угла наклона касательной, то, по определению, он равен производной функции в данной точке, то есть tg  = у₀ = f(x₀, y₀).

Как видно из рисунка, точным решением на рассмотренном шаге должна быть точка С, однако получена точка В с координатами (х₁, у₁), которая лежит уже на другой интегральной кривой 2. Это означает, что данный метод имеет погрешность вычислений. На рисунке эта погрешность обозначена . Нетрудно заметить, что погрешность можно существенно снизить, если уменьшить шаг h. Точность вычислений при этом возрастёт, но увеличится число шагов и объем вычислений.

y 1 2 C y1   B y0 A y0 0 x0 x1 x h

Рис. 9. Геометрическая интерпретация метода Эйлера.

Рассмотрим пример. Пусть требуется найти решение уравнения уу + 2х² = 0 на интервале [1,2] при условии у(1) = 3. Представим уравнение в виде у = -2х²/у. Разобьем интервал [1,2] на десять шагов с шагом h = 0,1. Воспользуемся расчетной формулой (4.5).

Первый шаг (i = 0):

х₁ = х₀ + h = 1 + 0,1 = 1,1;

y₁ = y₀ + h  f(y₀, x₀) = 3 + 0,1(-21²)/3 = 2,93.

Второй шаг (i = 1):

х₂ = х₁ + h = 1,1 + 0,1 = 1,2;

y₂ = y₁ + h  f(y₁, x₁) = 2,93 + 0,1(-21,1²)/2,93 = 2,85.

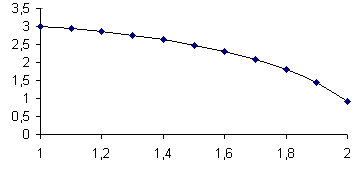
Аналогично можно найти значения искомой величины на всём интервале. Результаты расчета сведём в таблицу:

х	1,0	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	2,0
у	3,00	2,93	2,85	2,75	2,63	2,48	2,30	2,07	1,79	1,43	0,93

Y

. Полученные данные позволяют построить график искомой функции на заданном интервале изменения аргумента:

Р X ис. 10

Программа решения рассмотренного уравнения методом Эйлера может иметь следующий вид:

program ODU; {Решение ОДУ методом Эйлера}

var

i,n:integer;x,y,h:real;

function f(a,b:real):real;

begin

f:=(-2*sqr(a))/b;

end;

begin

writeln ('Введите начальные значения x и y'); readln(x,y);

writeln ('Введите шаг'); readln(h);

writeln ('Введите число шагов'); readln(n);

writeln (' РЕШЕНИЕ');

writeln (' x y');

writeln (x:8:3,y:8:3);

for i:=1 to n do

begin

y:=y+h*f(x,y);

x:=x+h;

writeln (x:8:3,y:8:3);

end;

end.

Задания. Методом Эйлера найти численное решение задачи Коши для данного дифференциального уравнения и начального условия на отрезке с шагом .

Таблица 7

№ варианта	Уравнение	Начальное условие	a	b
0			4	5
1
2			-1	-0,1
3
4			1	2
5			0	1
6			1	2
7			-1	-0,1
8			1	2
9			0	1

.