
- •Раздел 10. Числовые и функциональные ряды
- •Глава 1. Числовые ряды
- •§ 3. Основные свойства сходящихся рядов
- •Глава 2. Cходимость числовых рядов с неотрицательными членами
- •§ 2. Признаки сравнения для рядов с неотрицательными членами
- •§ 3. Интегральный признак Коши
- •§ 4. Признак Даламбера и радикальный признак Коши
- •Глава 3. Сходимость знакопеременных рядов
- •§ 2. Знакопеременные ряды. Абсолютная и условная сходимость
- •Свойства абсолютно сходящихся рядов
- •Глава 4. Функциональные ряды. Степенные ряды
- •§ 1. Понятие функционального ряда, его области сходимости
- •§ 2. Степенные ряды. Теорема Абеля. Интервал сходимости
- •§ 3. Разложение функции в степенной ряд. Ряд Тейлора
- •§ 4. Разложение некоторых элементарных функций в ряды Маклорена
§ 2. Степенные ряды. Теорема Абеля. Интервал сходимости
Определение 2.1. Функциональный ряд вида
![]() (2.1)
(2.1)
называется степенным рядом, числа an R, n 1, 2, называются коэффициентами степенного ряда.
Замечание 2.1. Степенные ряды замечательны прежде всего тем, что их члены un(x) an(x x0)n, n 1, 2, , являются сравнительно простыми функ-циями. Частичные суммы степенного ряда Sn(x) – многочлены от переменной х степени не выше п. Относительная простота un(x) и Sn(x) служит причиной мно-гих свойств, присущих степенным рядам, которыми не обладают другие функ-циональные ряды. Область сходимости степенного ряда никогда не является пустым множеством, поскольку ряд (2.1) обязательно сходится в точке x0.
В ряде (2.1) сделаем замену переменной: y x x0, получим ряд:
 . (2.2)
. (2.2)
Очевидно, что исследование сходимости ряда (2.1) эквивалентно исследованию сходимости ряда (2.2). Поэтому далее будем рассматривать ряды вида (2.2), но для обозначения переменной будем использовать букву x, а не y.
В основе теории степенных рядов лежит следующая теорема.
Теорема 2.1 (теорема Абеля). Если степенной ряд
![]() (2.3)
(2.3)
сходится
при x = x0 0,
то он сходится, и притом абсолютно, при
![]() x:
|x| |x0|.
x:
|x| |x0|.
Если степенной ряд (2.3) расходится при x x0, то он расходится и при всяком x: |x| |x0|.
►Доказательство проведём в два этапа.
1) Пусть
ряд (2.3) сходится в некоторой точке x0![]() ,
иными словами, сходится числовой ряд
,
иными словами, сходится числовой ряд
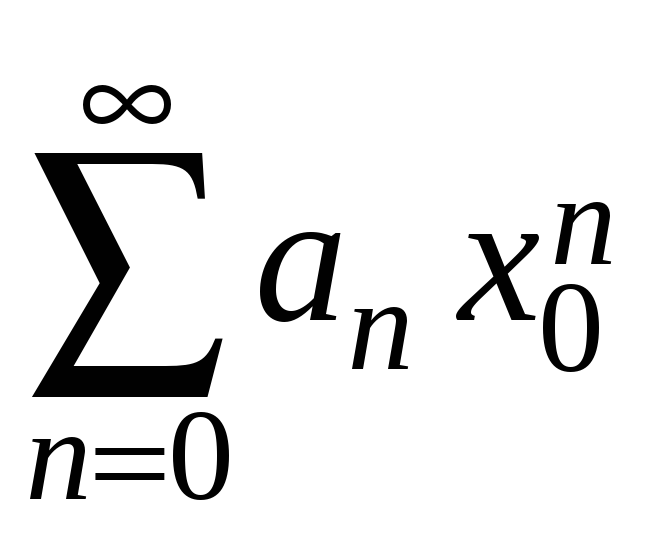 . (2.4)
. (2.4)
Общий
член ряда (2.4) стремится к нулю при n ,
и потому последовательность
 ограничена, т. е.
существует такая постоянная M 0,
что
ограничена, т. е.
существует такая постоянная M 0,
что
![]() ,
n 1, 2, .
,
n 1, 2, .
В силу этого для общего члена ряда (2.3) получается следующая оценка:
![]() .
.
Если
|x| |x0|,
то ряд
![]() есть геометрический ряд со знаменателем
есть геометрический ряд со знаменателем
![]() ,
поэтому он сходится. Но тогда по признаку
сравнения сходится и ряд
,
поэтому он сходится. Но тогда по признаку
сравнения сходится и ряд
 ,
что означает абсолютную сходимость
ряда (2.3) при |x| |x0|.
,
что означает абсолютную сходимость
ряда (2.3) при |x| |x0|.
2) Пусть теперь ряд расходится при некотором x x0. Но тогда он будет расходиться при любом x, удовлетворяющем условию |x| |x0|. В самом деле, если бы при каком-либо x, удовлетворяющем этому условию, ряд (2.3) сходился, то в силу только что доказанной первой части теоремы он должен был бы сходиться в точке x0, так как |x0| |x|. Но это противоречит условию, что в точке x0 ряд расходится. Следовательно, ряд расходится и в точке x.◄
Теорема Абеля позволяет судить о расположении точек сходимости и расходимости степенного ряда (2.3).
Следствие из теоремы 2.1. Пусть в точке x0 0 ряд (2.3) сходится, но тогда ряд (2.3) сходится в каждой точке интервала (|x0|, |x0|). Если же ряд (2.3) расходится в точке x1, то он расходится в интервалах (, |x1|), (|x1|, ).
И
степенного
ряда Рис.
2.1. К понятию радиуса сходимости
Рис.
2.1. К понятию радиуса сходимости
Замечание 2.2. Для ряда (2.1) интервал сходимости имеет вид (x0 R, x0 R).
Замечание 2.3. На концах интервала сходимости (т. е. при x ±R для ряда (2.3), при x = x0 ±R для ряда (2.1)) ряд может или сходиться или расходиться. Здесь необходимо дополнительное исследование.
Замечание 2.4. У некоторых рядов интервал сходимости вырождается в точку (R 0), а у других совпадает со всей осью (R )
При нахождении радиуса сходимости степенного ряда во многих случаях можно использовать признаки сходимости для знакоположительных рядов.
Пример
2.1.
Найти область сходимости ряда
 .
.
►Данный ряд является рядом с неортицательными членами. Применим к данному ряду, например, радикальный признак Коши. Так как
![]() ,
,
то ряд будет абсолютно сходиться, если
![]()
![]()
![]() .
.
Исследуем
поведение ряда на концах интервала
сходимости. Пусть
![]() ,
тогда ряд
,
тогда ряд
![]() расходится, так как его общий член не
стремится к нулю. Таким образом, область
сходимости ряда:
расходится, так как его общий член не
стремится к нулю. Таким образом, область
сходимости ряда:
![]() .◄
.◄
