Раздел 10. Числовые и функциональные ряды

Теория рядов – один из важнейших разделов математики. В нём исследую-тся вопросы, связанные с перенесением свойств элементарных алгебраических операций, а также правил дифференцирования и интегрирования (известных для конечного числа слагаемых) на случай бесконечного числа слагаемых.

Теория рядов широко используется в приближённых вычислениях. С её по-мощью составляются таблицы значений функций, вычисляются определённые интегралы от функций, у которых первообразные не являются элементарными функциями, находятся решения классов дифференциальных уравнений, весьма важных для физики, техники и экономики.

Глава 1. Числовые ряды

§ 3. Основные свойства сходящихся рядов

Свойство 1. Пусть ряд

(3.1)

сходится, S − его сумма, а c – некоторое вещественное число. Тогда ряд

(3.2)

тоже сходится, и его сумма равна cS.

Свойство 2. Если ряды и сходятся, а A и B – их суммы, то ряд , называемый суммой (разностью) данных рядов, тоже сходится, и его сумма равна A  B.

Замечание 3.1. Раскрывать скобки в сходящемся ряде, вообще говоря, нельзя. Например, ряд (1  1)  (1  1)    (1  1)   сходится, и его сумма S  0; если же раскрыть скобки, то получится расходящийся ряд: 1  1  1  1   .

Докажем, например, свойство 1.

►Пусть S_n и − n-е частичные суммы рядов (3.1) и (3.2) соответственно. Имеем:   ca₁    ca_n  c(a₁    a_n)  cS_n. По условию ряд (3.1) сходится к сумме S, поэтому . Но тогда   ряд (3.2) сходится, его сумма равна cS.◄

Замечание 3.2. Если ряд сходится, а ряд расходится, то сумма этих рядов есть ряд расходящийся. Действительно, если предположить сходимость ряда , то по свойству 2 сходящихся рядов будет сходиться ряд 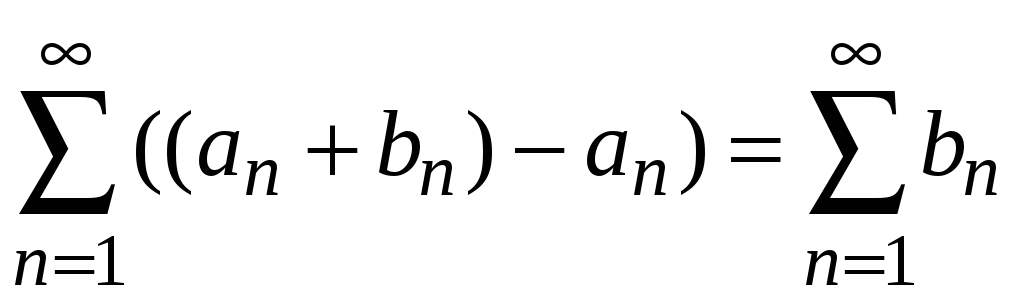, а по условию он расходится;

Замечание 3.3. Из расходимости рядов и расходимость ряда не следует. Так, если , , ряды и расходятся, а ряд сходится. Однако, если , , то ряд будет расходиться.

Определение 3.1. Пусть дан ряд (3.1) и любое натуральное число m. Ряд

a_m1  a_m2    a_mk = (3.3)

называется остатком ряда (3.1) после m-го члена.

Теорема 3.1. Ряд (3.1) и его остаток (3.3) после m-го члена сходятся или расходятся одновременно.

►Обозначим n-ю частичную сумму ряда (3.1) через , а k-ю частичную сумму ряда (3.3) – через . При имеем:

. (3.4)

Здесь S_m − некоторое число, так как m фиксировано.

Пусть ряд (3.1) сходится, и его сумма равна S. Из этого следует, что существует конечный . Но тогда из (3.4) следует, что существует конечный , причём . Последнее означает, что ряд (3.3) сходится и его сумма  равна S − S_m. Итак, из сходимости ряда (3.1) следует сходимость ряда (3.3).

Пусть теперь ряд (3.3) сходится и его сумма равна . Это означает, что существует конечный . Переходя в (3.4) к пределу при k   получаем

,

следовательно, ряд (3.1) сходится, и его сумма S равна . Итак, из сходимости ряда (3.3) следует сходимость ряда (3.1).

Вторая часть теоремы доказывается от противного. Пусть один из рядов (3.1), (3.3) расходится. Требуется доказать, что тогда расходится и другой ряд. Допустим, что он сходится. Но тогда, по доказанному выше должен сходиться и первый ряд, что противоречит условию. Значит, ряды (3.1) и (3.3) расходятся одновременно.◄

Следствие 1 из теоремы 3.1. Отбрасывание любого числа первых членов ряда не влияет на его сходимость.

Следствие 2 из теоремы 3.1. Для того, чтобы сходился ряд (3.1) необходимо и достаточно чтобы его остаток после n-го члена стремился к нулю при .