
статья Модели распространения радиосигнала
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА «СЕТИ СВЯЗИ И ТЕЛЕКОММУНИКАЦИОННЫЕ СИСТЕМЫ»
А.В. Абилов
РАСПРОСТРАНЕНИЕ РАДИОВОЛН В СЕТЯХ ПОДВИЖНОЙ СВЯЗИ
Теоретический материал и задачи для практических занятий
Ижевск 2001

УДК 621.396.218 (07) А15
Р е ц е н з е н т А.С. Бобков, зам. генерального директора по эксплуатации
ЗАО «Цифровые сети Удмуртии-900»
Абилов А.В.
А15 Распространение радиоволн в сетях подвижной связи: Теоретический материал и задачи для практических занятий. – Ижевск: Изд-во ИжГТУ, 2001. – 24 с.: ил.
Пособие содержит материал по теории электромагнитного поля, теории антенн, описание моделей распространения радиоволн в сетях подвижной связи для различных условий, а также замирания радиосигнала.
Для студентов вузов, обучающихся по направлению «Телекоммуникации».
♥ Абилов А.В., 2001 ♥ Издательство ИжГТУ, 2001
2

Содержание
1.Основы теории электромагнитного поля……………………………………4
2.Основы теории антенн……………………………………………………….8
3.Модели распространения радиосигнала
3.1.Модель распространения радиосигнала
всвободном пространстве……………………………………………..12
3.2.Распространение радиосигнала в реальных условиях……………….13
3.3.Двухлучевая модель распространения радиосигнала………………..14
3.4.Модель Окамуры……………………………………………………….15
3.5.Модель Хаты……………………………………………………………17
3.6.Модель COST231–Hata………………………………………………...18
3.7.Заказные модели………………………………………………………..18
4.Замирания радиосигнала
4.1.Медленные замирания…………………………………………………19
4.2.Запас на замирание для логарифмически нормального распределения уровня сигнала………………………………………...20
4.3.Быстрые замирания…………………………………………………….21
4.4.Запас на замирание для рэлеевского распределения
уровня сигнала………………………………………………………….22
Задачи……………………………………………………………………………23
Литература………………………………………………………………………24
Распространение радиоволн в сетях подвижной связи |
3 |
1. Основы теории электромагнитного поля
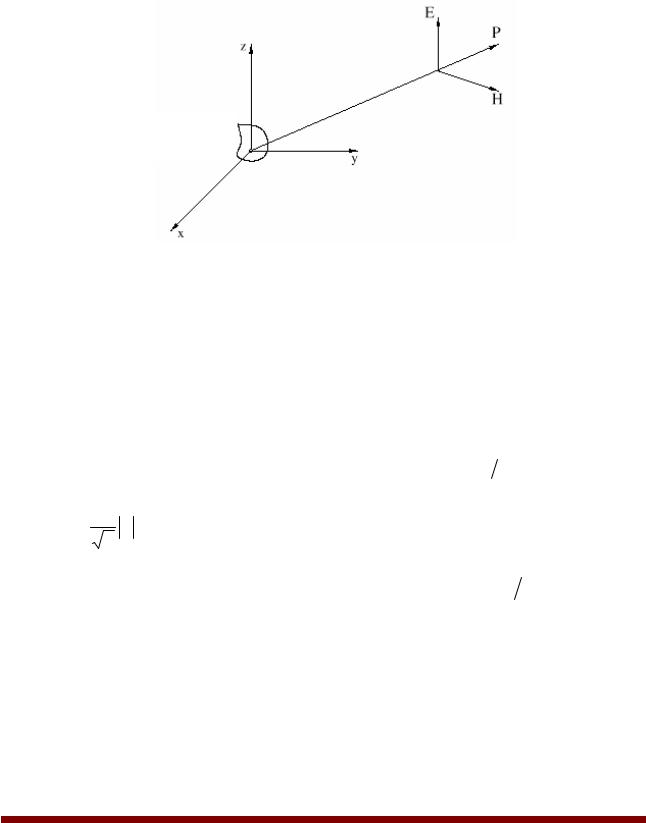
Антенна, на вход которой подается переменный ток, порождает электромагнитное поле. Излучаемый антенной радиосигнал состоит из электрического
Ε(x,y,z,t) и магнитного H(x, y, z,t) полей (рис. 1.1).
Источник
излучения
Рис. 1.1. Векторы электрического и магнитного полей в пространстве
Векторы E и H ортогональны. Так как векторы гармонически изменяются во времени, то вектор электрического поля можно записать в следующей форме:
E(t) = E sin(2πft), |
(1.1) |
||||||||
где E – амплитуда вектора электрического поля. |
|
||||||||
Напряженность электрического поля (RMSвеличина), В м |
|
||||||||
ERMS = 1 E . |
(1.2) |
||||||||
2 |
|
|
|
||||||
Плотность потока мощности электромагнитного поля, Вт м2 |
|
||||||||
Φ = 1 |
|
E |
|
|
|
H |
|
. |
(1.3) |
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поляризация электрического поля определяет ориентацию его вектора в пространстве. Различают линейную, круговую и эллиптическую поляризации
(рис. 1.2).
При линейной поляризации направление вектора электрического поля не меняется во времени. Если его вектор направлен вертикально по отношению к
4

земле, то имеет место вертикальная поляризация. Если горизонтально, то горизонтальная поляризация.
При круговой поляризации направление вектора электрического поля гармонически изменяется во времени, но его амплитуда остается величиной постоянной.
Когда вместе с изменением направления вектора электрического поля меняется его амплитуда, то в этом случае имеет место эллиптическая поля-
ризация.
Рис. 1.2. Линейная, круговая и эллиптическая поляризации электромагнитной волны
В свободном пространстве как электрическое, так и магнитное поле переносят одинаковое количество энергии
ε0 |
|
E |
|
2 = µ0 |
|
H |
|
2 , |
(1.4) |
|
|
|
|
где ε0 ≈ 8,86 10−12 – электрическая постоянная свободного пространства, Ф м; µ0 ≈ 1,256 10−6 – магнитная постоянная свободного пространства, Гн
м; µ0 ≈ 1,256 10−6 – магнитная постоянная свободного пространства, Гн м.
м.
Сопротивление свободного пространства, Ом
Z0 = |
µ0 = 337 . |
(1.5) |
|
ε0 |
|
Скорость распространения электромагнитных колебаний в свободном пространстве, м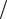 c
c
v = c = |
1 |
≈ 3 108 . |
(1.6) |
|
µ0 ε0 |
|
|
Распространение радиоволн в сетях подвижной связи |
5 |
||

Плотность потока мощности электромагнитного поля
|
E 2 |
|
|
Φ = |
RMS |
= Z0 H RMS2 . |
(1.7) |
|
|||
|
Z0 |
|
|
Распространение волны может быть представлено лучами, исходящими от источника в направлении распространения сигнала. На значительном расстоянии до передающей антенны источник радиосигнала можно рассматривать как точечный источник. В этом случае в пределах небольшой области пространства лучи расположены почти параллельно друг к другу, следовательно, можно считать, что волна является плоской (рис. 1.2).
Фронт волны B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
RC |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RD |
|
|
|
|
||
|
|
|
|
|
RB |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кубическая область |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Фронт волны A |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
пространства |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(d << RD) |
|
|
|
|
RA |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Источник |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Лучи |
|
|
|
d |
|
|
|
|
||
|
излучения |
|
|
|
|
|
|
|
|
|
|
|
|
Окружность, |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
касательная к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
грани куба |
|
Рис. 1.3. Фронт волны и лучи сигнала в свободном пространстве
Пусть электромагнитная волна распространяется вдоль оси x (рис. 1.4).
E0
x
z
H y
Ez H 0
y
6
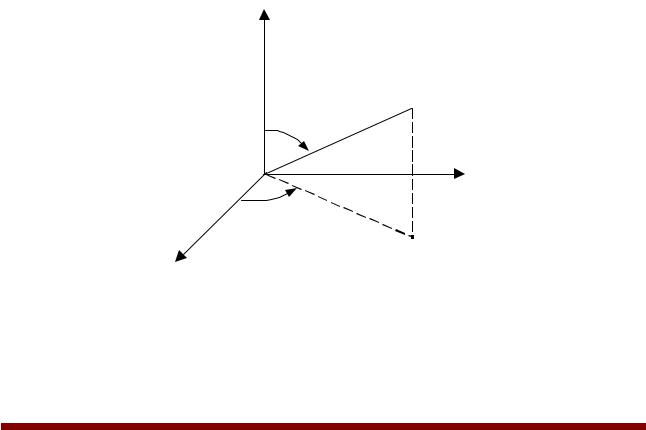
Рис. 1.4. Пространственные отношения векторов электромагнитной волны
E(x,t) и H(x,t) – векторы электрического и магнитного полей соответственно. Для плоской волны эти векторы расположены перпендикулярно направлению распространения:
Ex (x,t) = 0 , H x (x,t) = 0 . |
(1.8) |
Для составляющих векторов также очевидны следующие соотношения:
Ez (x,t) = E0 sin(2πf (t − τ )) = E0 sin(2πft − βx), |
(1.9) |
Ey (x,t) = 0, |
(1.10) |
H y (x,t) = H0 sin(2πf (t − τ )) = H0 sin(2πft − βx), |
(1.11) |
H z (x,t) = 0 , |
(1.12) |
где τ = x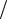 v = x
v = x λf – задержка распространения сигнала;
λf – задержка распространения сигнала;
v – скорость распространения сигнала; β = 2π  λ – коэффициент изменения фазы.
λ – коэффициент изменения фазы.
При рассмотрении распространения электромагнитных волн удобно использовать полярные координаты (r,θ ,φ ), как показано на рис. 1.5.
z |
|
θ |
r |
|
y |
φ |
|
x
Рис. 1.5. Угол места и угол азимута в трехмерном пространстве
Распространение радиоволн в сетях подвижной связи |
7 |

2. Основы теории антенн
Для передачи радиосигнала необходимо наличие антенной системы. Можно представить, что антенна излучает одинаковое количество энергии во всех направлениях сферы. Такая антенна является гипотетической (мнимой), так как ее не существует в природе, и называется изотропной антенной.
Плотность потока мощности Φ сигнала, излучаемого передающей антенной полностью определяется распределением энергии электромагнитного поля в про-
странстве и выражается в Вт м2 (мощность на единицу площади). Строго говоря,
м2 (мощность на единицу площади). Строго говоря,
величина Φ является функцией трехмерного свободного пространства. Поскольку изотропная антенна во всех направлениях излучает равное количество энергии, то длянее Φ можетрассматриваться какфункциятолькорасстояния Φ i (d ).
Если полную мощность, подводимую к изотропной антенне обозначить через Pt , то справедливы следующие равенства:
P = 4πd 2 |
Φ |
(d ), [ Вт], |
|
(2.1) |
|||
t |
i |
|
|
|
|
||
Φi (d ) = |
|
Pt |
|
, [ Вт м2 |
]. |
(2.2) |
|
4πd 2 |
|||||||
|
|
|
|
||||
Антенны, используемые на практике, не являются изотропными. В них энергия, излучаемая в трехмерном пространстве, распределена не равномерно. Это свойство антенн используется для улучшения их характеристик.
Коэффициент направленного действия (КНД) рассматриваемой антенны
Gt (θ ,φ ) определяется как отношение плотности потока мощности, которую она
порождает в заданном направлении к плотности потока мощности, порождаемой изотропной антенной в том же направлении при условии, что обе антенны излучают одинаковую мощность.
Коэффициент усиления антенны Gt равен КНД антенны в направлении максимального излучения энергии:
Gt = max{Gt (θ ,φ )}. |
(2.3) |
Величину Gt также называют коэффициентом усиления изотропного излуча-
теля и измеряют в дБи (dBi). Однако иногда коэффициент усиления антенны измеряется по отношению к полуволновому диполю и имеет размерность дБд (dBd). Полуволновой диполь имеет коэффициент усиления 2,15 дБ по отношению к изотропной антенне (дБи). Следовательно, коэффициент усиления Gt , измеряемый в
дБд, на 2,15 дБ меньше, чем если он измеряется в дБи для той же самой антенны:
x (дБд) = x +2,15 (дБи). |
(2.4) |
8

С учетом коэффициента усиления передающей антенны, измеряемого в разах,
Φ = |
PtGt |
, [ Вт м2 ]. |
(2.5) |
|
4πd 2 |
||||
|
|
|
||
Если коэффициент усиления антенны Gt |
измеряется в дБи, то произведение |
|||
Pt Gt называется эквивалентной мощностью изотропного излучателя (EIRP –
equivalent isotropically radiated power) и также измеряется в дБи.
Для Gt , измеряемого в дБд, произведение Pt Gt называется эффективной
мощностью излучения (ERP – effective radiated power) и тоже измеряется в дБд.
Следовательно, величина ERP на 2,15 дБ меньше величины EIRP для той же антенны.
Ток, протекающий в передающей антенне, порождает электромагнитную энергию, излучаемую в пространство. В свою очередь, если приемная антенна подвергается воздействию электромагнитного поля, в ней возникает электрический ток. Следовательно, один и тот же тип антенны может использоваться как для передачи, так и для приема сигнала. Тогда для приемной антенны также справедливы такие параметры, как коэффициент направленного действия и коэффициент усиления антенны.
Пусть на приемную антенну воздействует электромагнитная волна с плотностью потока мощности Φ в ее окрестности. Тогда мощность сигнала на вы-
ходе антенны Pr определяется из выражения |
|
Pr = ΦAr , [ Вт]. |
(2.6) |
Коэффициент Ar называется эффективным поперечным сечением приемной
антенны. Он характеризует эффективность преобразования электромагнитной энергии в электрическую и определяется из выражения
Ar = Gr λ2 , [м2 ], (2.7) 4π
где Gr – коэффициент усиления приемной антенны, (раз); λ – длина электромагнитной волны, (м).
Как на входе, так и на выходе антенны мощность сигнала часто измеряют
как уровень по отношению к эталонной величине мощности: |
|
|||
дБВт (dBW): |
10lg(P Po ), |
где Po |
= 1 Вт; |
|
дБм (dBm): |
10lg(P Po ), |
где Po |
= 1 мВт. |
|
Рассмотрим |
полуволновой диполь в |
сферической системе |
координат |
|
(рис. 2.1). |
|
|
|
|
Распространение радиоволн в сетях подвижной связи |
9 |
|||

|
|
|
|
|
|
|
θ |
= 0ο |
|
|
|
|
φ = 90ο |
||||
|
|
||||
|
|
|
|
|
Диполь |
θ |
|
|
|
λ |
|
φ |
|
φ = 0ο |
|
2 |
|
θ = 90ο |
|
|
Рис. 2.1. Полуволновой диполь в сферической системе координат
На рис. 2.2 представлена диаграмма направленности (ДН) такой антенны в вертикальной плоскости, относительно которой φ = 0 . ДН антенны характери-
зует пространственное распределение излучаемой энергии.
θ
Диаграмма
направленности
Рис. 2.2. Диаграмма направленности полуволнового диполя в вертикальной плоскости
При вращении вертикальной плоскости относительно оси антенны ее ДН не меняется. Такая антенна называется всенаправленной (omnidirectional).
Ширина главного лепестка ДН определяется как угловая ширина, ограниченная коэффициентом направленного действия 3 дБ относительно максимума.
Уровень боковых лепестков определяется по отношению к максимуму главного лепестка и выражается в дБ относительного него.
На рис. 2.3 представлена диаграмма направленности реальной всенаправленной антенны, а на рис. 2.4 – секторизованной антенны.
10
