18 Обобщённая формула прямоугольников

Построение.

Простейшая квадратурная формула получается при использовании интерполяционного многочлена нулевой степени.

Фиксируем и заменяем подинтегральную функцию интерполяционным многочленом нулевой степени, который совпадает со значением : . Тогда

(59)

Частные случаи:

- формула левых прямоугольников

- формула правых прямоугольников

- формула средних прямоугольников.

19 Обобщённая формула трапеции

Построение.

Аппроксимируем подинтегральную функцию интерполяционным многочленом 1-й степени

Тогда 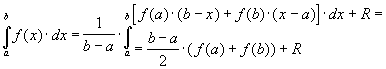(66)

Геометрический смысл этой формулы - площадь трапеции, у которой одна из сторон это хорда, соединяющая точки графика , соответствующие и .

20 Обобщённая формула симпсона

Построение.

Аппроксимируем подинтегральную функцию интерполяционным многочленом 2-й степени, совпадающим с в точках .

(70)

Заменяя Ошибка! Закладка не определена., где и интегрируя (70), получаем

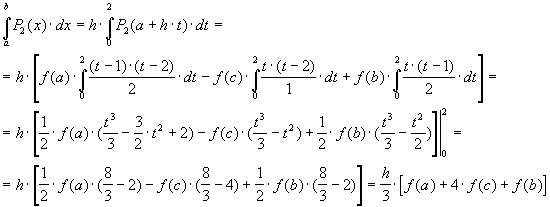
Таким образом, квадратурная формула имеет вид:

(71)

Она называется квадратурной формулой Симпсона или формулой парабол (т. к. дуга кривой заменяется на дугу кривой второго порядка).

21 Гаусса квадратурная формула

ГАУССА КВАДРАТУРНАЯ ФОРМУЛА

квадратурная формула вида

в к-рой узлы x_i и веса с; подбираются так, чтобы формула была точна для функций

где - заданные линейно независимые функции (пределы интегрирования могут быть и бесконечными). Г. к. ф. введены К. Гауссом (см. [1]) для

Полученная им общая формула, точная для произвольного многочлена степени не выше 2n- 1, имеет вид

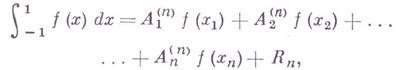
где - корни Лежандра многочлена. и определяются по формулам

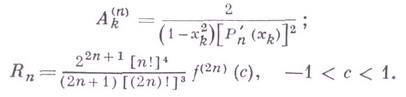
Применяется в тех случаях, когда подинтегральная функция достаточно гладкая, а выигрыш в числе узлов крайне существен: напр., если определяется из дорогостоящих экспериментов, или при вычислении кратных интегралов как повторных. При практическом применении в таких случаях очень важен удачный подбор весовой функции и функций

22 Чебышева квадратурная формула

ЧЕБЫШЕВА КВАДРАТУРНАЯ ФОРМУЛА

- интерполяционная квадратурная формула с равными коэффициентами:

Весовая функция равна 1, промежуток интегрирования конечен и считается совпадающим с [ - 1, 1]. Число параметров, определяющих квадратурную формулу (*), равно N+l (Nузлов и значение коэффициента С). Параметры определяются требованием, чтобы квадратурная формула (*) была точна для всех многочленов степени не выше Nили, что то же самое, для одночленов 1, х, х²,... , x^N. Параметр Снаходится из условия, что квадратурная формула точна для f(x) =1,и равен 2/N. Узлы x₁.... , x_N оказываются действительными лишь при N=1(1)7 и N=9. При N=1(1)7 узлы вычислил П. Л. Чебышев. При среди узлов Ч. к. ф. всегда имеются комплексные (см. [1]). Алгебраич. степень точности Ч. к. ф. равна Nпри Nнечетном и равна N+1 при Nчетном. Формула (*) предложена П. Л. Чебышевым в 1873.

25 Метод Эйлера-Коши

Метод Эйлера-Коши также относится к методам второго порядка и тоже требует двукратного вычисления функции f (x, y):

y⁰_i+1 = y_i + hf (x_i, y_i);

y_i+1 = y_i+ (f (x_i, y_i) + f (x_i+1, y⁰_i+1)) h/2 .

Методы Эйлера относятся к группе с общим названием метода Рунге-Кутта, к этой же группе принадлежит и метод, называемый методом Рунге-Кутта четвертого порядка. Согласно этому методу для вычисления одного значения функции y(x) необходимо вычислить функцию f(x, y) в четырех точках:

K1_i = f (x_i, y_i);

K2_i = f (x_i + h/2, y_i + K1_i/2);

K3_i= f (x_i + h/2, y_i + K2_i/2);

K4_i= f (x_i + h, y_i + K3_i);

y_i+1 = y_i + h (K1_i + 2K2_i + 2K3_i + K4_i)/6.

Погрешность этого метода пропорциональна h⁴, т.е. |y_i-y_i*| < O(h⁴).