Содержание отчета

1. Передаточная функция заданного объекта.

2. М-файл расчета параметров передаточной функции дискретной модели объекта.

3. Расчет параметров апериодического регулятора.

4. Модель дискретной системы и осциллограммы переходных процессов, полученные в результате выполнения пп. 4 - 9.

5. Анализ полученных осциллограмм и общий вывод о влиянии периода квантования на адекватность дискретной модели цифро-аналоговому варианту.

Контрольные вопросы

1. Как изменяется величина управляющего воздействия на объект при изменении периода дискретизации?

2. Изменится ли длительность переходного процесса в системе с апериодическим регулятором при изменении вида входного сигнала относительно линейно-нарастающего сигнала, использованного при моделировании?

3. Какие критерии качества учитываются при определении апериодического регулятора?

4. Какие меры следует предпринять для устранения скрытых колебаний управляемого сигнала?

Лабораторная работа № 7 исследование робастной устойчивости линейных сау

Цель работы:

1. анализ качества регуляторов, обеспечивающих робастную устойчивость;

2) исследование робастной устойчивости САУ с различными регуляторами.

Теоретическая подготовка для выполнения данной лабораторной работы включает изучение раздела курса лекций, разделов рекомендованной литературы, посвященных исследованию робастной устойчивости и вопросам проектирования регуляторов, обеспечивающих робастную устойчивость САУ.

Порядок выполнения работы

4. Вызвать систему MATLAB 6.1.

5. Создайте в рабочем окне системы MATLAB информацию о передаточной функции объекта

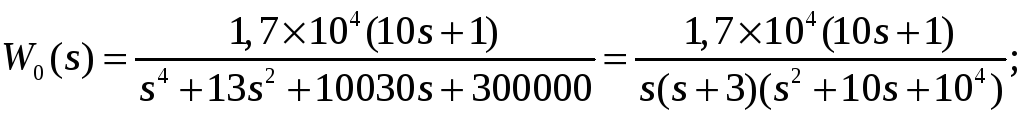
используя m-файл

6. Создайте модель первого регулятора

где величина выбирается из таблицы 7.1.

Таблица 7.1

№ вар.	1	2	3	4	5	6
	0,1	0,15	0,2	0,25	0,35	0,4
,с	0,04	0,025	0,013	0,033	0,02	0,03
,с	0,05	0,04	0,025	0,05	0,04	0,045
,с	0,025	0,025	0,02	0,029	0,029	0,038
,с	0,1	0,033	0,067	0,02	0,05	0,06

4. Создайте модель замкнутой системы с первым регулятором

5. Создайте модель второго регулятора

и модель замкнутой системы со вторым регулятором, реализуя m-файл

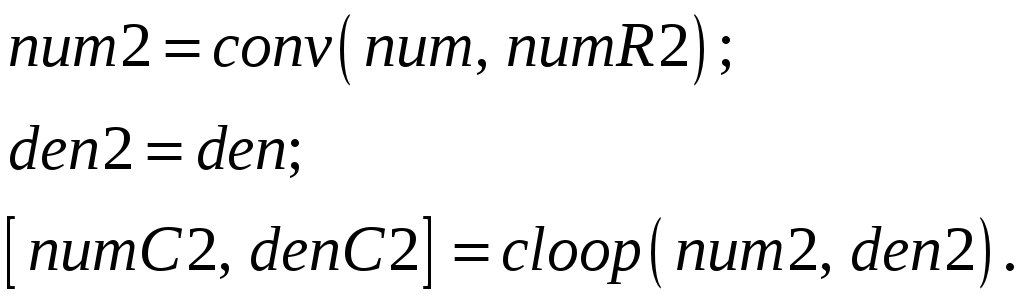
6. Создайте модель третьего регулятора

и модель замкнутой системы с третьим регулятором

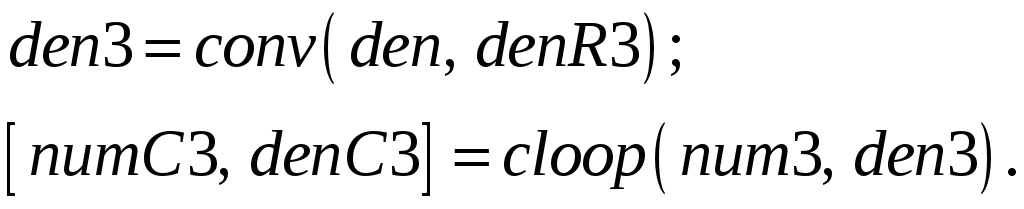
7. Создайте модель четвертого регулятора

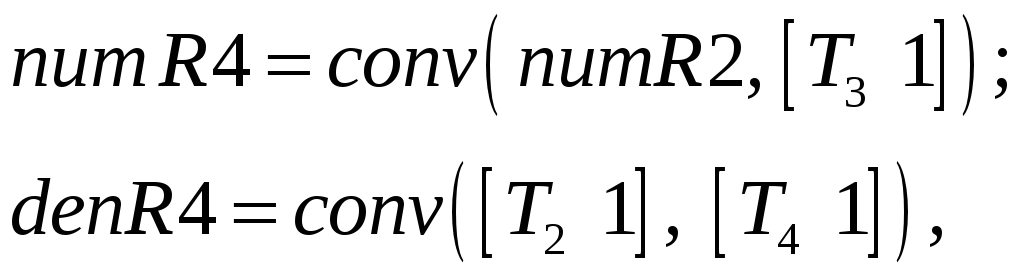
и модель замкнутой системы с четвертым регулятором

8. Построить обратные логарифмические частотные характеристики замкнутых номинальных систем, используя последовательно m-файлы:

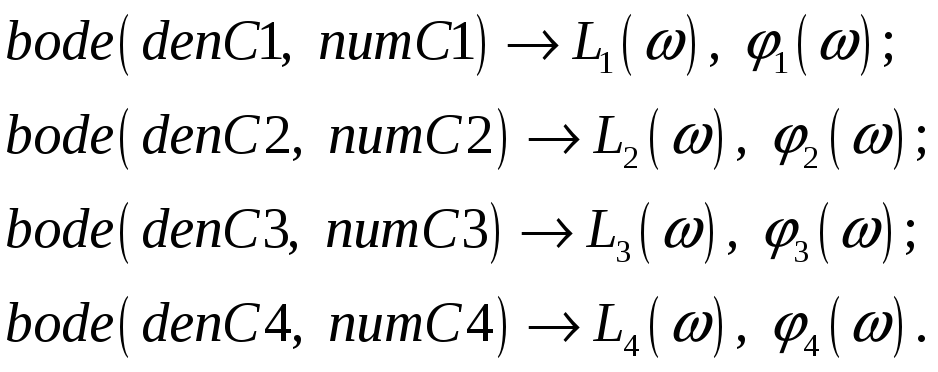
9. Для каждой из обратных логарифмических частотных характеристик определить значение величины , называемой гарантированной границей робастной устойчивости, причем

Отсюда Лучшим считается регулятор, для которого имеет место .

10. Исследовать робастную устойчивость систем. Для этого следует последовательно сформировать четыре системы в соответствии с методикой, описанной в пп. 2 - 9, заменив номинальную передаточную функцию объекта на передаточную функцию возмущенного объекта управления

где оставив передаточные функции регуляторов без изменений. Для каждой из систем следует построить диаграммы Боде и воспользоваться логарифмическим критерием устойчивости.

11. Создать математическую модель относительной неопределенности

и построить логарифмические частотные характеристики неопределенности:

12. Исследовать робастную устойчивость:

а) если условие выполняется, то регулятор обеспечивает робастную устойчивость;

б) если имеется хотя бы одна частота , при которой , то ый регулятор не обеспечивает робастной устойчивости.