Контрольные вопросы

1. Укажите местоположение корней характеристического уравнения для устойчивой системы, неустойчивой системы и системы на границе устойчивости.

2. Каким образом для анализа устойчивости можно использовать критерии устойчивости непрерывных систем, такие как критерий Гурвица, критерий Найквиста?

3. Является ли устойчивой цифровая система, характеристическое уравнение которой имеет вид

ЛАБОРАТОРНАЯ РАБОТА № 3

АНАЛИЗ УСТОЙЧИВОСТИ ДИСКРЕТНЫХ СИСТЕМ

ПО УРАВНЕНИЯМ СОСТОЯНИЯ

Цель работы:

получение навыков определения устойчивости цифровой системы на основе матричных критериев Зубова и Ляпунова.

Теоретическая подготовка к выполнению данной лабораторной работы состоит в изучении материалов курса лекций и (или) соответствующих разделов рекомендованной литературы, где рассматриваются критерии устойчивости Зубова и Ляпунова для дискретных систем.

Порядок выполнения лабораторной работы

1. Вызвать matlab 6.Х.

2. Сформировать систему

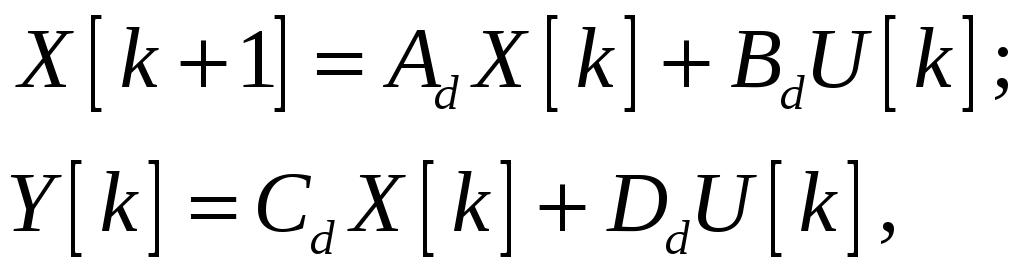(1)

используя оператор MATLAB

где матрицы системы (1) формируются случайным образом, но так, чтобы собственные значения матрицы удовлетворяли бы условию равномерной асимптотической устойчивости решения однородного разностного уравнения , n- номер подгруппы.

3.Инициализировать матрицы и в виде

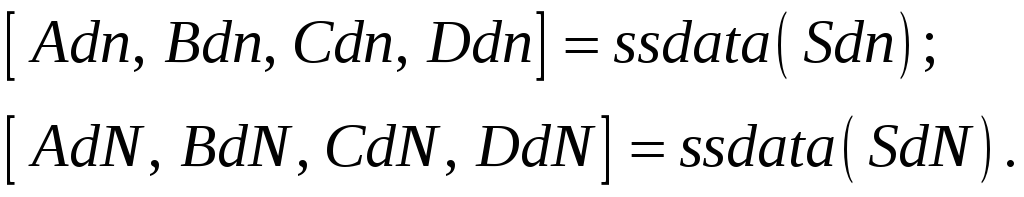(2)

4. Вычислить векторы и убедиться в выполнении условий и устойчивости, если пренебрежимо мал.

5. Вычислить матрицы 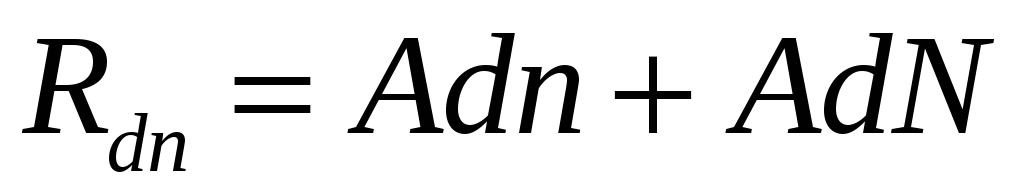и 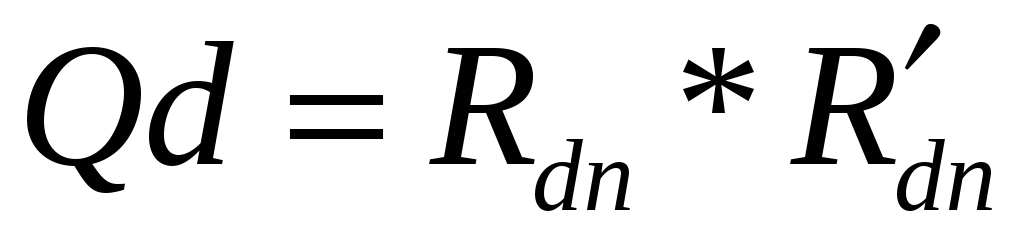и вектор

(3)

5. Найти решение матричного уравнения Ляпунова, используя оператор MATLAB

(4)

5. Проверить качество полученного решения путем вычисления матрицы

(5)

Если элементы матрицы пренебрежимо малы, то найденное решение является качественным.

5. Для качественного решения вычислить собственные значения 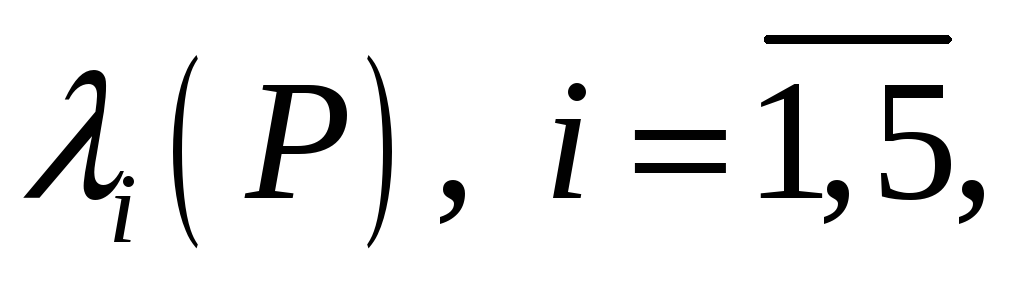которые должны быть вещественными и строго положительными, а 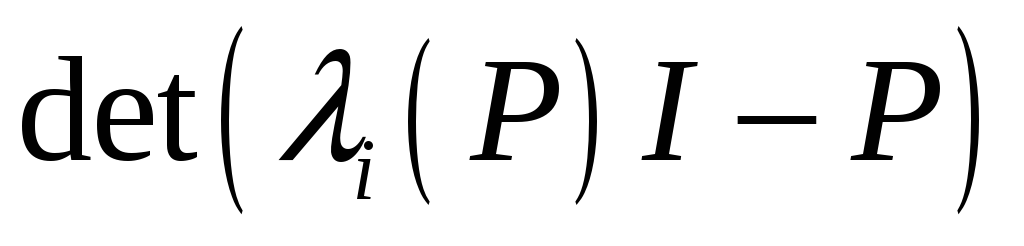- пренебрежимо мал.

9. Если условие (5) не выполняется, то достаточное условие устойчивости не выполняется.

10. Исследовать устойчивость тривиального решения разностного уравнения

(6)

Использовать условия критерия Зубова, если:

а)еслигде (7)

то все собственные значения матрицы удовлетворяют условию устойчивости;

б)если

то выполняются условия неустойчивости;

в)если

то система находится на границе устойчивости. Символ обозначает какую-либо из норм матрицы .

Содержание отчета

1. Сформированные матрицы

2. Вектор 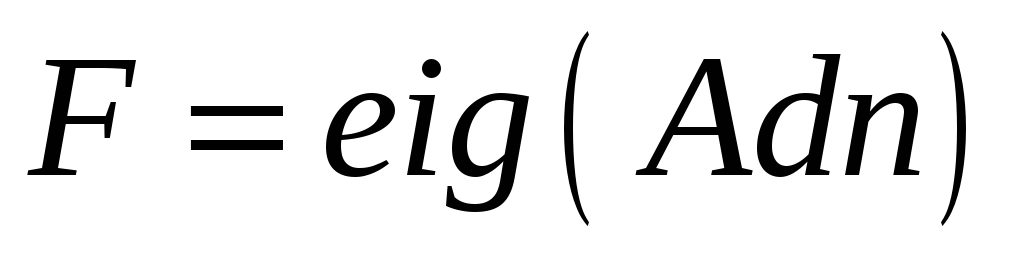и анализ условий устойчивости.

3. Матрицы

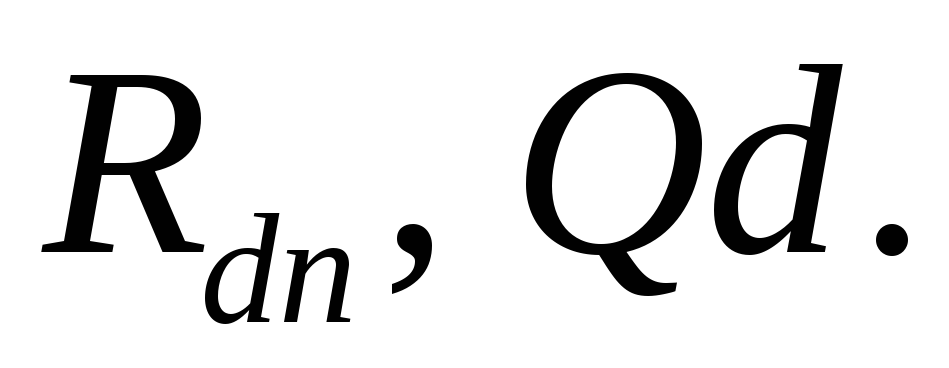
4. Вектор и анализ положительной определенности матрицы .

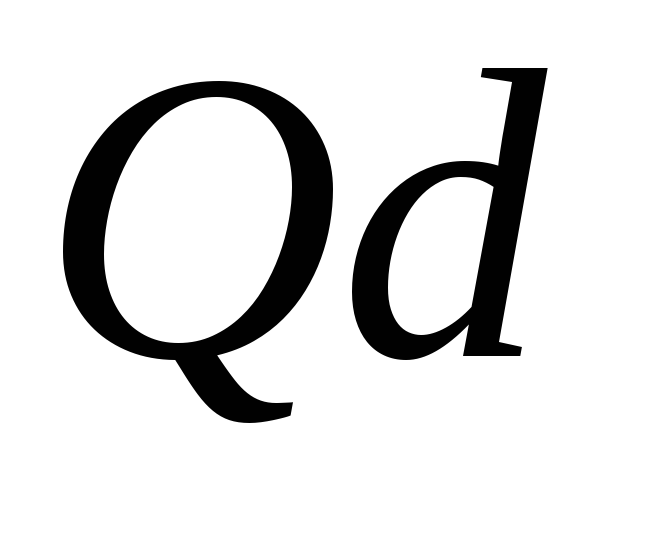5. Матрицу 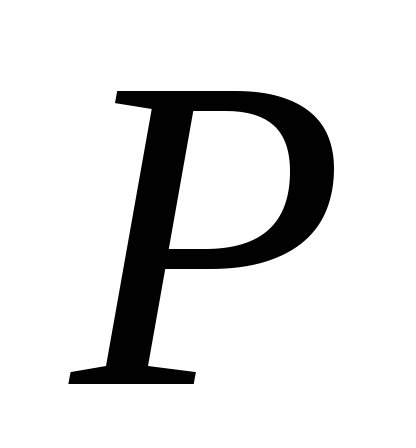решения матричного уравнения Ляпунова (4) дискретных систем.

6. Результаты проверки и анализ качества решения уравнения (4).

7. Анализ собственных значений матрицы .

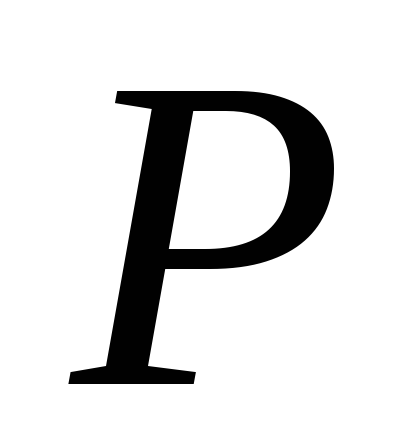8. Вывод об устойчивости системы

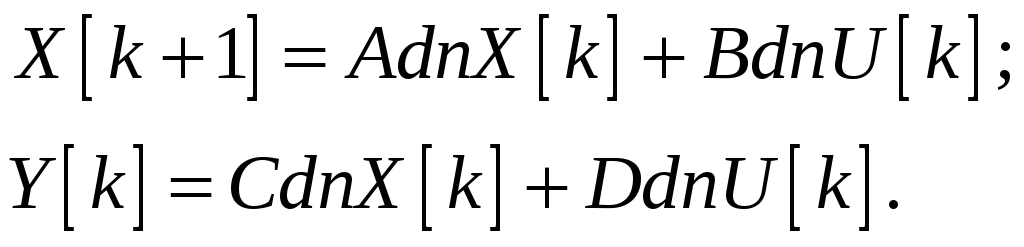(8)

9. Результаты вычисления матриц , анализ нормы этих матриц, вывод об устойчивости системы (8).