
- •Некоторые сведенья из математики
- •Комплексная форма представления гармонических функций
- •Линейные уравнения с постоянными коэффициентами Общее решение.
- •Принцип действия систем автоматического управления.
- •Структурная схема следящей системы
- •Сопровождение цели «на проходе».
- •Автоматическая подстройка частоты.
- •Структурная схема цифровой следящей системы.
- •Автоматическая система управления качеством.
- •Классификация систем управления
- •1. По основным видам уравнений динамики процессов управления:
- •2. Линейные системы разделяются на:
- •3. По характеру передачи сигналов различают:
- •Типовые звенья систем ау
- •Использование символической формы.
- •Амплитудно-фазовая частотная характеристика.
- •Логарифмическая амплитудная частотная характеристика (лах) и
- •Апериодическое звено второго порядка.
- •5) Критерии качества переходного процесса во времени
- •Амплитудные частотные характеристики замкнутой системы
- •6) Дифференциальное уравнение замкнутой системы
- •Диаграмма Вышнерадского
- •7) Устойчивость сау
- •1. Критерий Гурвица [5]
- •2. Критерий Михайлова
- •3. Критерий Найквиста
- •8) Введение в теорию нелинейных сау
- •Метод гармонической линеаризации
- •Коэффициент передачи нелинейного элемента по первой гармонике
- •Введение в теорию нелинейных сау
- •Гармоническая линеаризация типовых звеньев
- •9) Пространство состояний (фазовое пространство)
- •Сау с идеальным реле и жесткой обратной связью
- •Сау с идеальным реле и гибкой обратной связью
- •Реле с петлей гистерезиса
- •10) Понятие о дискретных системах Введение
- •Виды квантования непрерывных сигналов
- •1.3 Классификация дискретных сау
- •Примеры дискретных систем
- •2. Математические основы теории дв-систем
- •2.1 Решетчатые функции
- •2.2 Синусоидальные решетчатые функции
- •Дополнение.
- •2.3 Прямые и обратные разности
1. Критерий Гурвица [5]
Исторически этот критерий появился первым (1875 - Раус, 1895 - Гурвиц). Задача состояла в том, чтобы, не вычисляя корни характеристического уравнения, что при отсутствии вычислительной техники и при высокой степени уравнения сложно, найти условия устойчивости характеристического многочлена.
Приводится без доказательства.
Из коэффициентов многочлена составим квадратную матрице размера nn (так называемую матрицу Гурвица [3]), по следующему правилу
По диагонали выписываются коэффициенты характеристического уравнения, начиная с a1. Строки матрицы заполняются коэффициентами: влево от диагонали записываются коэффициенты с возрастающими индексами, а справа - с убывающими. Остальные элементы матрицы - нули.
Ниже представлена матрица для n=6 (a0>0):

В первой строке слева места нет, а с меньшим индексом всего один коэффициент a0. В последней строке коэффициентов с возрастающими индексами нет, а для коэффициентов с убывающими индексами справа нет места.
В литературе встречается и правило составления транспонированной матрицы [1].
Из матрицы образуют так называемые определители Гурвица - главные диагональные миноры матрицы:
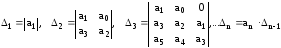
Формулировка критерия:
Для устойчивости системы необходимо и достаточно, чтобы a0>0 и определители Гурвица были положительными.
Заметим, что при вычислении каждого последующего определителя используются уже вычисленные значения предыдущих определителей. Это сокращает объем вычислений.
Пример.
Пусть передаточная функция разомкнутой системы
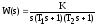 .
.
Передаточная функция замкнутой системы:
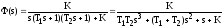
Тогда дифференциальное уравнение свободного движения системы после ее замыкания
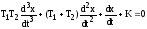 .
.
Следовательно, a0=T1T2; a1= (T1+T2); a2=1; a3=K.
Матрица Гурвица системы третьего порядка:
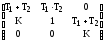
Условие
a0>0
выполняется и, следовательно, 1=
T1+T2>0.
Условие 
2=
T1+T2-KT1T2>0
равносильно условию
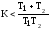 .
.
Третий определитель 3=K2, что равносильно условию K>0. Таким образом, усиление системы должно лежать в пределах (рис. 1)
0<
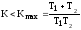 .
.
При K<0 в обратная связь положительная, а при K>Kmax теряется устойчивость. На рис.1 изображены переходные процессы в системе при различных коэффициентах усиления системы.
Недостатки критерия:
- в случае неустойчивости системы критерий не дает ответа на то, как нужно изменить параметры системы, чтобы сделать ее устойчивой;
- в случае устойчивой системы критерий не дает информации о качестве регулирования и о запасах устойчивости.
В силу этих обстоятельств в инженерной практике чаще используются более удобные с этой точки зрения критерии.
2. Критерий Михайлова
Характеристическое уравнение имеет n корней, которые могут быть действительными, мнимыми и комплексными. Некоторые из n корней могут оказаться равными между собой (кратными). Комплексные корни всегда попарно сопряженные, при нечетном n имеется хотя бы один действительный корень [6].
Как уже отмечалось, для того чтобы система была устойчивой необходимо, чтобы действительные части всех корней были отрицательными, то есть, чтобы все корни характеристического уравнения лежали левее мнимой оси плоскости комплексного переменного .
D() - характеристический многочлен линейной системы n-ного порядка с положительными коэффициентами. Произведя подстановку =j, получим
D(j)=X()+jY(),
X() - четная функция , Y() - нечетная функция .
Формулировка критерия устойчивости Михайлова [1]:
Для устойчивости линейной системы n-ного порядка необходимо и достаточно, чтобы изменение аргумента функции D(j) при изменении от 0 до равнялось бы n/2, то есть
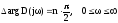 .
.
Доказательство [5].
Пусть i (i =1, 2, .., n) - корни уравнения D(j)=0. Тогда можно записать
D(j)=a0(j-1)(j-2).. (j-n),
D(j)=a0j-1j-2 … j-n,
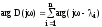 .
.
Покажем, что при изменении от =0 до = каждый отрицательный действительный корень дает приращение аргумента +/2, а каждая пара комплексных корней - приращение аргумента +.
Напомним,
что разность двух векторов - это вектор,
соединяющий их концы, направленный к
уменьшаемому вектору.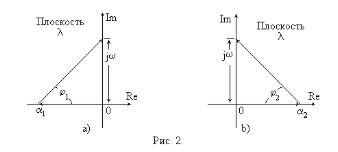
На рис.2a действительный корень 1 =1, причем 1<0. При возрастании от нуля до бесконечности аргумент разности векторов j-1 (угол 1 ) изменяется от нуля (при =0) до +/2 (положительное направление отсчета углов - против часовой стрелки). На рис.2b корень 2=2 причем 2>0. При возрастании от нуля до бесконечности аргумент разности векторов j-2 изменяется от нуля (при =0) до минус /2.
На рис.3 представлен случай, когда два сопряженных корня имеют отрицательные действительные части.
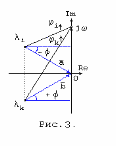
При
=0 углы поворота
векторов
 и
и
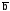 равны - и +,
соответственно. При
угол поворота вектора
равны - и +,
соответственно. При
угол поворота вектора
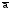 составит /2+,
а угол поворота вектора
составит /2+,
а угол поворота вектора
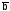 /2-,
таким образом, суммарное изменение
аргумента, вносимое двумя комплексно
сопряженными корнями, расположенными
в левой полуплоскости
составит угол .
/2-,
таким образом, суммарное изменение
аргумента, вносимое двумя комплексно
сопряженными корнями, расположенными
в левой полуплоскости
составит угол .
Очевидно, что пара комплексно сопряженных корней в правой полуплоскости внесет изменение аргумента равное -.
Таким образом доказана справедливость критерия Михайлова.
Геометрическая интерпретация критерия.
При изменении от 0 до + годограф вектора D(j), начиная с точки, расположенной на положительной части действительной оси, проходит последовательно в положительном направлении n квадрантов. Начало годографа на положительной действительной оси следует из положительности коэффициентов устойчивой системы (необходимое, но недостаточное условие устойчивости).
Если система находится на границе устойчивости (имеются корни вида 0+j), то годограф пройдет через начало координат. При этом очертания годографа оказываются такими, что малые его деформации в начале координат могут сделать его удовлетворяющим критерию Михайлова.
Если система неустойчива, то малые деформации не могут дать такого эффекта.
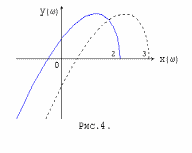
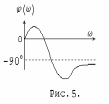
На рис.4 представлены годографы Михайлова для двух астатических систем третьего порядка с постоянными времени T1=0.5c, T2=2c (критический коэффициент усиления Kmax=2.5) для K=2 и K=3 (выше критического) . При оба годографа асимптотически приближаются к оси абсцисс. При K=2 угол поворота вектора D(j) равен +270 градусов, при K=3 - угол поворота изменяется не монотонно и при оказывается равным минус 90 градусов. На рис.5 представлена качественная зависимость для K=3.
Другая формулировка критерия состоит в том, что корни уравнений X()=0 и Y()=0, полученных из равенства D(j)=X()+jY(), должны чередоваться. Первый корень =0 имеет нечетный многочлен Y(). Удаленность корней X()=0 и Y()=0 друг от друга характеризует запас устойчивости САУ.
