Дополнительные задания
1 Вариант
-
Даны уравнения двух сторон параллелограмма
,
точка пересечения его диагоналей
M(3;–1).
Найти уравнения двух других сторон. -
Записать уравнения прямой в канонической форме:
-
Написать уравнения плоскости, проходящей через точку
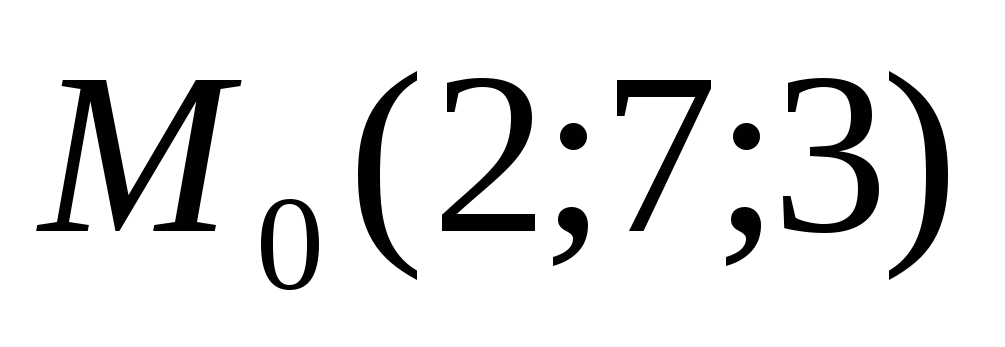перпендикулярно прямой, которая через
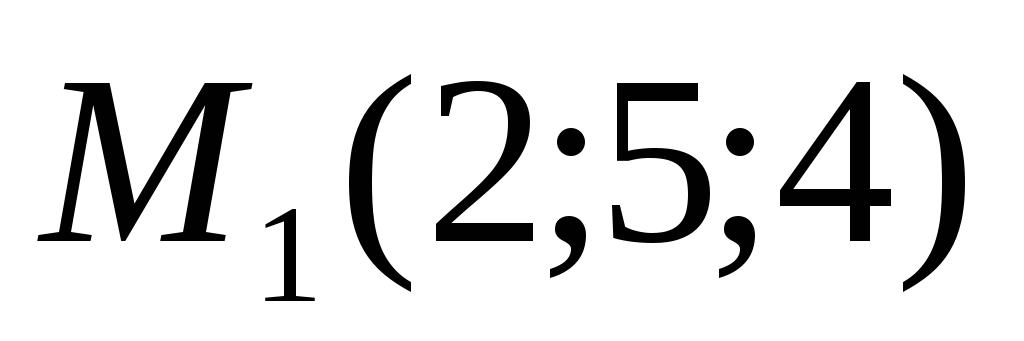точки
и
. -
Даны вершины треугольника
,
,
.
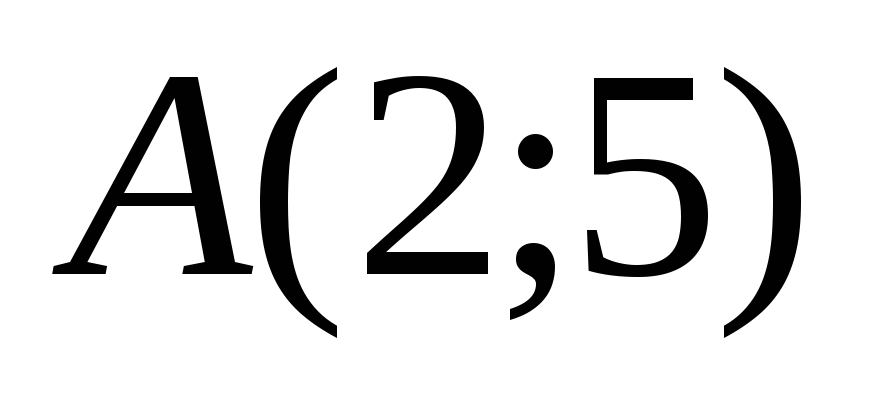Найти уравнение медианы АМ. -
Даны координаты вершин пирамиды:
,
,
,
.
Найти:
а) длину ребра
;
б)
угол между ребрами
и
;
с) объем пирамиды.
2 Вариант
-
Даны вершины треугольника АВС:
,
,
.
Найти расстояние от точки С
до прямой АВ. -
Записать уравнения прямых, проходящих через точку
под углом
к прямой
. -
Написать уравнение плоскости, параллельной плоскости
и проходящей через точку
. -
Составить каноническое уравнение прямой, проходящей через точку
перпендикулярно к прямым
-
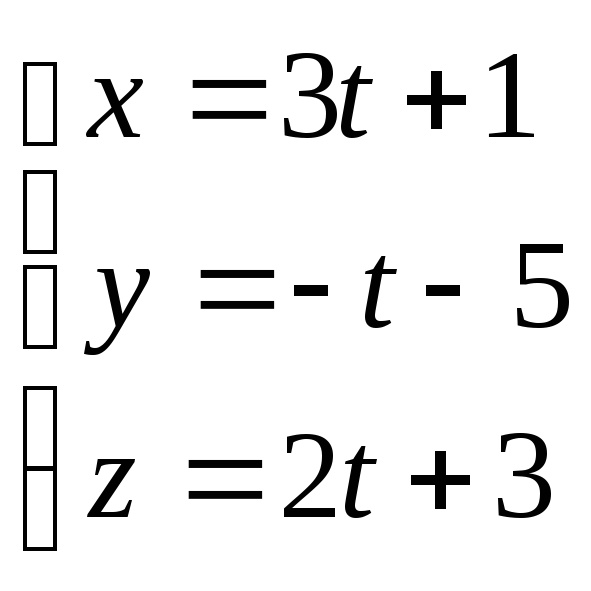
Найти угол между диагоналями параллелограмма, построенного на векторах
,
,
где
,
,
.
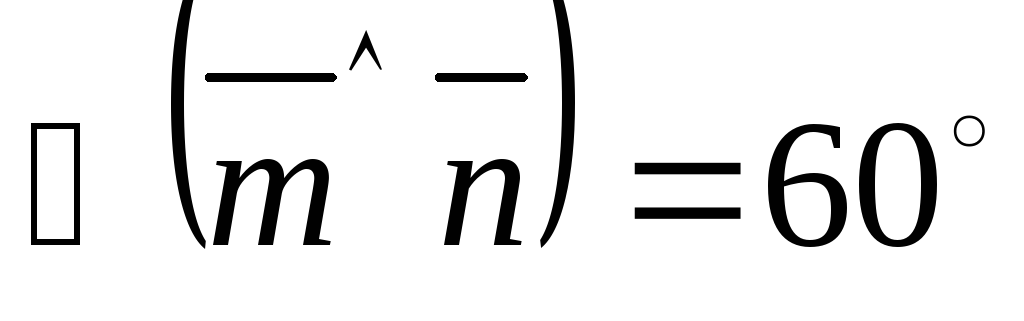3 Вариант
-
Найти точку пересечения прямой и плоскости
-
Составить уравнение плоскости, проходящей через точки
и
параллельно вектору
. -
Записать уравнение прямой в канонической форме
-
Доказать, что четырехугольник ABCD – трапеция, если
,
,
,
. -
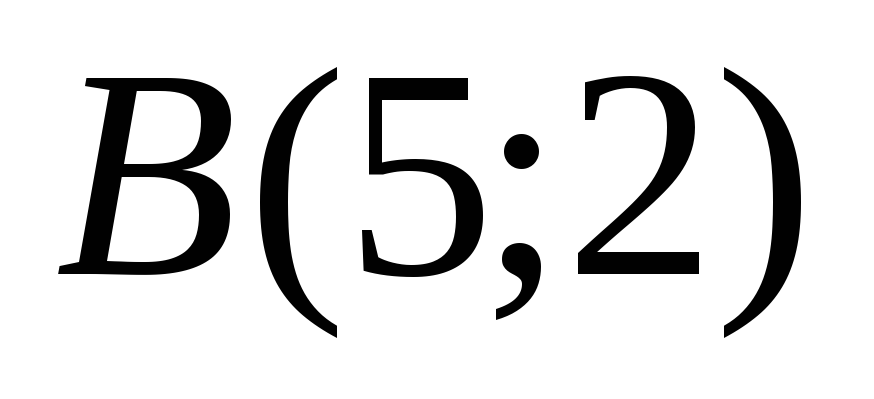Даны три вектора:
,
,
.
Найти вектор
,
удовлетворяющий условиям
,
,
4 Вариант
1.
Заданы вершины пирамиды
,
,
,
.
Найти расстояние от точки D
до плоскости ABC.
2.
Найти уравнение прямой, проходящей
через точку
параллельно MN,
если
,
.
3.
Определить, при каком значении С
плоскости
и
будут перпендикулярны.
4.
Доказать, что прямая
параллельна плоскости
.
5.
Даны вершины треугольника
,
и
.
Определить его внешний угол при вершине
А.
5 Вариант
1.
Доказать, что прямая
лежит в плоскости
.
2.
Составить параметрические уравнения
медианы треугольника с вершинами
,
,
,
проведенной из вершины С.
3.
Составить уравнение плоскости, проходящей
через точку
и прямую
,
,
.
4.
Даны вершины треугольника АВС:
,
,
.
Найти уравнение высоты СH.
5.
Векторы
и
взаимно перпендикулярны, а вектор
образует с ними углы, равные
.
Зная, что
и
,
найти
.
6 Вариант
1.
Написать уравнение плоскости, проходящей
через прямую
и точку
.
Найти угол между искомой плоскостью и
плоскостью
.
2.
Найти острый угол между диагоналями
параллелограмма, построенного на
векторах
и
.
3.
Найти точку О,
пересечения диагоналей четырехугольника
АВСD,
если
,
,
,
.
4.
Найти расстояние между плоскостями
и
.
5.
Даны координаты вершин пирамиды АВСD:
,
,
,
.
Найти проекцию вектора АВ
на вектор СD.
7 Вариант
1.
Даны две вершины треугольника АВС:
и
и точка
,
пересечения его высот. Найти вершину
С.
2.
Найти угол
наклона прямой, проходящей через точки
и
к плоскости 3х
– 4у
+10 = 0.
3. Написать уравнение плоскости, проходящей через точку перпендикулярно к плоскостям х + 2у –2z + 4 = 0 и х–2у+ z–4 = 0.
4.
Написать уравнения прямой, проходящей
через точку
и параллельно вектору
в
канонической и параметрической формах.
5.
Даны точки О(0;0;0),
А(5;2;0),
В(2;5;0),
С(1;2;4)
вершины пирамиды. Вычислить ее объем,
площадь грани ABC
и высоту пирамиды, опущенную на эту
грань
.