
- •СамарсКий государственНый университет путей сообщения
- •Содержание
- •Аналитическая геометрия
- •I. Прямые и плоскости
- •1. Плоскость
- •Задание 1
- •Задание 2
- •Задание 3
- •2. Прямая в пространстве. Прямая и плоскость
- •Задание 4
- •Задание 5
- •Задание 6
- •3. Прямая на плоскости
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Дополнительные задания
- •1 Вариант
- •2 Вариант
- •3 Вариант
- •4 Вариант
- •5 Вариант
- •6 Вариант
- •7 Вариант
- •8 Вариант
- •9 Вариант
- •10 Вариант
- •11 Вариант
- •12 Вариант
- •13 Вариант
- •14 Вариант
- •15 Вариант
- •16 Вариант
- •17 Вариант
- •18 Вариант
- •19 Вариант
- •20 Вариант
- •21 Вариант
- •22 Вариант
- •23 Вариант
- •24 Вариант
- •25 Вариант
- •26 Вариант
- •II Линии и поверхности второго порядка
- •1. Окружность и сфера
- •2. Эллипс и эллипсоид
- •3. Гипербола и гиперболоиды
- •4. Парабола и параболоиды
- •Задание 11
- •Задание 12
- •Задание 13
- •5. Цилиндры второго порядка. Конус второго порядка
- •6. Поверхности вращения
- •Задание 14
- •Задание 15
- •III. Линии, заданные уравнениями в полярных координатах и параметрическими уравнениями
- •1. Полярные координаты точки и уравнение линии в полярных координатах
- •Задание 16
- •Задание 17
- •Задание 18
- •2. Параметрические уравнения линии
- •Задание 19
Задание 5
Даны
точки
![]() ,
,
![]() ,
,
![]() и
и
![]() .
Составить уравнения:
.
Составить уравнения:
1)
прямой
![]() ;
;
2)
прямой
![]() ,
параллельной прямой
,
параллельной прямой
![]() ;
;
3)
прямой
![]() ,
перпендикулярной плоскости
,
перпендикулярной плоскости
![]() ;
;
4)
вычислить косинус угла между прямыми
![]() и
и
![]() ;
;
5)
вычислить синус угла между прямой
![]() и плоскостью
и плоскостью
![]() .
Найти координаты точки пересечения
этой прямой и плоскости;
.
Найти координаты точки пересечения
этой прямой и плоскости;
6)
найти расстояние от т.
![]() до прямой
до прямой
![]() .
.
1
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
4
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
5
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
6
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
7
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
8
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
9
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
10
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
11
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
12
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
13
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
14
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
15
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
16
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
17
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
18
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
19
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
20
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
21
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
22
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
23
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
24
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
25
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
26
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
27
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
28
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
29
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
30
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Задание 6
Решить следующие задачи.
1
вариант.
Доказать параллельность прямых
![]() и
и
![]() ,
,
![]() .
.
2
вариант.
Доказать, что прямая
![]() параллельна плоскости
параллельна плоскости
![]() ,
а прямая
,
а прямая
![]() лежит в этой плоскости.
лежит в этой плоскости.
3
вариант. Составить
уравнение прямой, проходящей через
точку
![]() и
образующей с осями координат углы,
соответственно равные
и
образующей с осями координат углы,
соответственно равные
![]() и
и
![]() .
.
4
вариант.
Доказать, что прямая
![]() перпендикулярна
к прямой
перпендикулярна
к прямой
 .
.
5
вариант.
Составить параметрические уравнения
медианы треугольника с вершинами
![]() ,
,
![]() ,
,
![]() проведенной из вершины С.
проведенной из вершины С.
6
вариант. При
каком значении п
прямая
![]() - параллельна прямой
- параллельна прямой
 .
.
7
вариант.
Найти точку пересечения прямой
![]() и плоскости
и плоскости
![]() .
.
8
вариант. Найти
проекцию точки
![]() на
плоскость
на
плоскость
![]() .
.
9
вариант. При
каком значении С
плоскости
![]() и
и
![]() перпендикулярны?
перпендикулярны?
10
вариант. При
каком значении А
плоскость
![]() параллельна прямой
параллельна прямой
![]() .
.
11
вариант. При
каких значениях m
и С прямая
![]() перпендикулярна к плоскости
перпендикулярна к плоскости![]() ?
?
12
вариант.
Составить уравнение прямой, проходящей
через начало координат параллельно
прямой
![]() ,
,
![]() ,
,
![]()
13
вариант. Проверить,
лежат ли на одной прямой точки
![]() ,
,
![]() и
и
![]() .
.
14
вариант.
Составить уравнение прямой, проходящей
через точку
![]() параллельно
прямой
параллельно
прямой
![]() ,
,
![]() .
.
15
вариант.
Составить уравнение прямой, проходящей
через точку
![]() перпендикулярно к прямым
перпендикулярно к прямым
![]() и
и
![]() .
.
16
вариант. При
каких значениях А
и В плоскость
![]() перпендикулярна к прямой
перпендикулярна к прямой
![]() ?
?
17
вариант.
Показать, что прямая
![]() параллельна плоскости
параллельна плоскости![]() ,
а прямая
,
а прямая
 ,
,
![]() ,
,
![]() лежит в этой плоскости.
лежит в этой плоскости.
18
вариант.
Составить уравнение плоскости, проходящей
через ось
Oz
и точку
![]() .
.
19
вариант.
Показать, что прямые
![]() и
и
![]() ,
,
![]() перпендикулярны.
перпендикулярны.
20
вариант. При
каком значении D
прямая
![]() ,
,
![]() пересекает ось Oz?
пересекает ось Oz?
21 вариант. При каком значении р прямые
 и
и
 параллельны?
параллельны?
22
вариант.
Найти точку пересечения прямой
![]() и плоскости
и плоскости
![]() .
.
23
вариант.
Составить уравнение плоскости, проходящей
через точку
![]() параллельно плоскости Oxz.
параллельно плоскости Oxz.
24
вариант.
Составить общие, уравнения прямой,
образованной пересечением плоскости
![]() с плоскостью, проходящей через ось Оу
и точку
с плоскостью, проходящей через ось Оу
и точку
![]() .
.
25
вариант. При
каких значениях В
и D
прямая
![]() ,
,
![]() лежит в плоскости Оху?
лежит в плоскости Оху?
26
вариант.
Составить уравнение плоскости, проходящей
через точку
![]() параллельно двум векторам
параллельно двум векторам
![]() и
и
![]() .
.
27
вариант.
Составить уравнения прямой, проходящей
через точку
![]() параллельно оси Ох.
параллельно оси Ох.
28
вариант. Составить
уравнения прямой, проходящей через
точку
![]() перпендикулярно к прямой
перпендикулярно к прямой
![]() .
.
29
вариант.
Составить
канонические уравнения прямой, проходящей
через точку
![]() перпендикулярно к прямым
перпендикулярно к прямым
![]() и
и
![]() ,
,
![]() ,
,
![]() .
.
30
вариант.
Найти точку,
симметричную точке
![]() относительно
прямой
относительно
прямой
![]() .
.
Решение типового варианта
Задание 4
Составить каноническое уравнения прямых и найти координаты любых двух точек для каждой прямой
1)
прямая задана точкой
![]() и направляющим вектором
и направляющим вектором
![]() ;
;
2)
прямая задана двумя точками
![]() и
и
![]() ;
;
3) прямая задана общими уравнениями
 .
.
Решение:
1) Составим каноническое уравнение прямой в пространстве по формуле (2.3):
![]() .
.
Для определения координат точек, принадлежащих этой прямой, запишем ее параметрические уравнения (2.2):

Придавая
t
произвольные значения можно определить
любое количество таких точек. Пусть
![]() ,
получаем т.
,
получаем т.
![]() ;
пусть теперь
;
пусть теперь
![]() ,
получаем вторую точку данной прямой
,
получаем вторую точку данной прямой
![]() .
.
2) Составим уравнение прямой в пространстве через две точки (2.4):
![]() или
или
![]() .
Заметим, что последнее выражение
.
Заметим, что последнее выражение
![]() следует рассматривать как уравнение
следует рассматривать как уравнение
![]() или
или
![]() .
Получаем частный случай расположения
прямой в пространстве – данная прямая
параллельна координатной плоскости
Оxy
(лежит в плоскости
.
Получаем частный случай расположения
прямой в пространстве – данная прямая
параллельна координатной плоскости
Оxy
(лежит в плоскости
![]() и описывается следующим уравнением
и описывается следующим уравнением
![]() ;
;
![]() или
или
![]() .
.
Запишем параметрические уравнения этой прямой:

при
![]() получаем т.
получаем т.
![]() ,
,
при
![]() получаем т.
получаем т.
![]() .
.
3)
Находим направляющий вектор
![]() прямой, заданной общими уравнениями
прямой, заданной общими уравнениями
 ,
,
где
![]() ,
,
![]() .
.
 ,
т.е.
,
т.е.
![]()
Найдем
теперь координаты любой точки этой
прямой. Т.к. уравнений в системе два, а
переменных три, одну из них задаем
произвольно, например
![]() ,
получаем
,
получаем
 .
.
Составим канонические уравнения:

при
![]() получаем т.
получаем т.
![]() ,
,
при
![]() получаем т.
получаем т.
![]() .
.
Задание 5
Даны
точки
![]() ,
,
![]() ,
,
![]() и
и
![]() .
Составить уравнения:
.
Составить уравнения:
1)
прямой
![]() ;
;
2)
прямой
![]() ,
параллельной прямой
,
параллельной прямой
![]() ;
;
3)
прямой
![]() ,
перпендикулярной плоскости
,
перпендикулярной плоскости
![]() ;
;
4)
вычислить косинус угла между прямыми
![]() и
и
![]() ;
;
5)
вычислить синус угла между прямой
![]() и плоскостью
и плоскостью
![]() .
Найти координаты точки пересечения
этой прямой и плоскости;
.
Найти координаты точки пересечения
этой прямой и плоскости;
6)
найти расстояние от т.
![]() до прямой
до прямой
![]() .
.
Решение:
1)
уравнение прямой
![]() составим по формуле (2.4)
составим по формуле (2.4)
![]() .
.
2)
уравнение прямой
![]() ,
параллельной прямой
,
параллельной прямой
![]() составим по формулам (2.2) и (2.3), учитывая
что ее направляющий вектор
составим по формулам (2.2) и (2.3), учитывая
что ее направляющий вектор
![]() :
:
канонические:
![]() ,
,
параметрические:

3)
составим сначала уравнение плоскости
![]() по формуле (1.4):
по формуле (1.4):
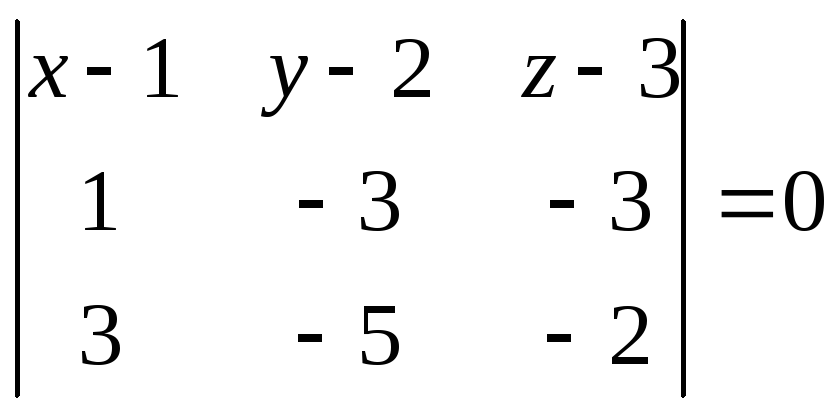 или
или
![]()
Нормальный
вектор этой плоскости
![]() является направляющим
является направляющим
![]() для прямой
для прямой
![]() ,
ее канонические уравнения составим по
формуле (2.3):
,
ее канонические уравнения составим по
формуле (2.3):
![]() .
.
4)
косинус угла между прямыми
![]() :
:
![]() и
и
![]() :
:
![]() вычислим как косинус угла между их
направляющими векторами
вычислим как косинус угла между их
направляющими векторами
![]() и
и
![]() по формуле (2.5):
по формуле (2.5):
![]() .
.
5)
Угол между прямой
![]() :
:
![]() и плоскостью
и плоскостью
![]() :
:
![]() вычислим через угол между векторами
вычислим через угол между векторами
![]() и
и
![]() по формуле (2.8):
по формуле (2.8):
![]() .
.
Для
вычисления координат точки пересечения
прямой
![]() и плоскости
и плоскости
![]() воспользуемся формулой (2.7):
воспользуемся формулой (2.7):
![]()
В
параметрические уравнения прямой
![]()
 подставляем
подставляем
![]() ,
получаем координаты точки пересечения
,
получаем координаты точки пересечения
![]() ,
что и так понятно из задания.
,
что и так понятно из задания.
6)
расстояние от т.
![]() до прямой
до прямой
![]() :
:
![]() найдем по формуле (2.6):
найдем по формуле (2.6):
![]() ,
,
![]() ,
,
![]() ,
,
 ,
,
![]() ,
,
![]() ,
,
![]() ед.
ед.
Задание
6. Найти
координаты точки
![]() симметричной точке
симметричной точке
![]() относительно плоскости
относительно плоскости
![]()
Решение:
Запишем
параметрические уравнения прямой
![]() ,
перпендикулярной данной плоскости,
т.е. вектор, нормальный для плоскости
,
перпендикулярной данной плоскости,
т.е. вектор, нормальный для плоскости
![]() является направляющим для прямой
является направляющим для прямой
![]() :
:

Подставляя
их в уравнение плоскости, находим
![]() :
:
![]() ,
откуда
,
откуда
![]() и, следовательно, точка М
пересечения прямой
и, следовательно, точка М
пересечения прямой
![]() с данной плоскостью
с данной плоскостью
![]() .
Т.к. т. М
является серединой отрезка
.
Т.к. т. М
является серединой отрезка
![]() ,
то верны равенства:
,
то верны равенства:
![]() ;
;
![]() ;
;
![]() ,
из которых находим координаты точки
,
из которых находим координаты точки
![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
