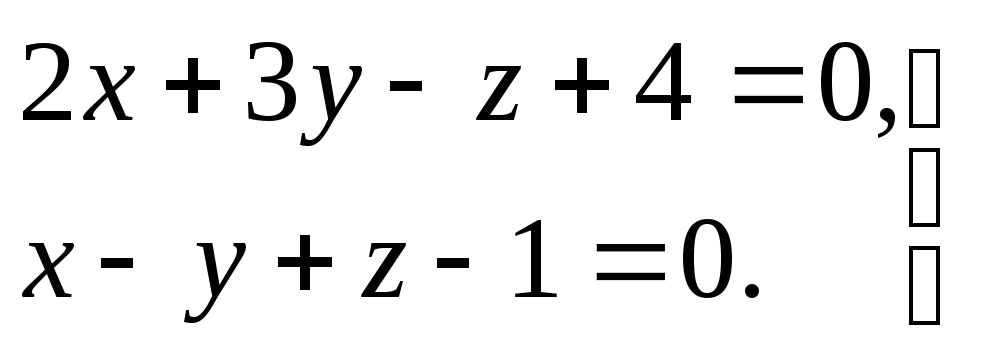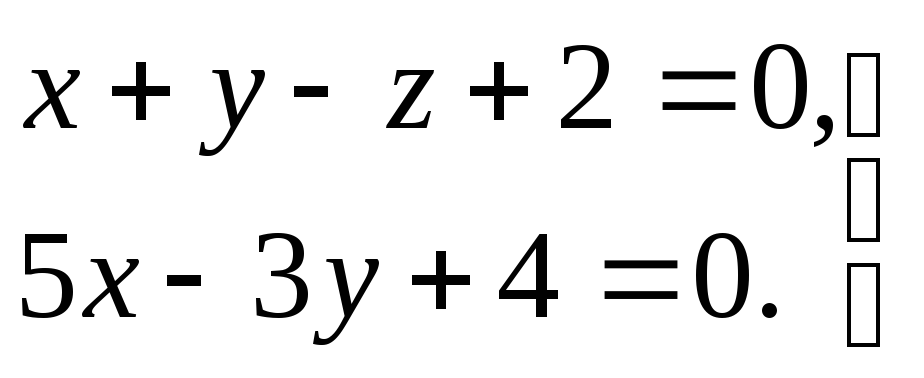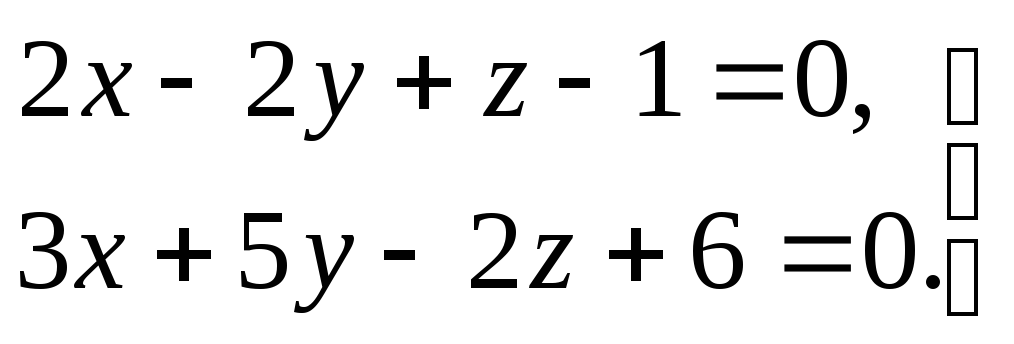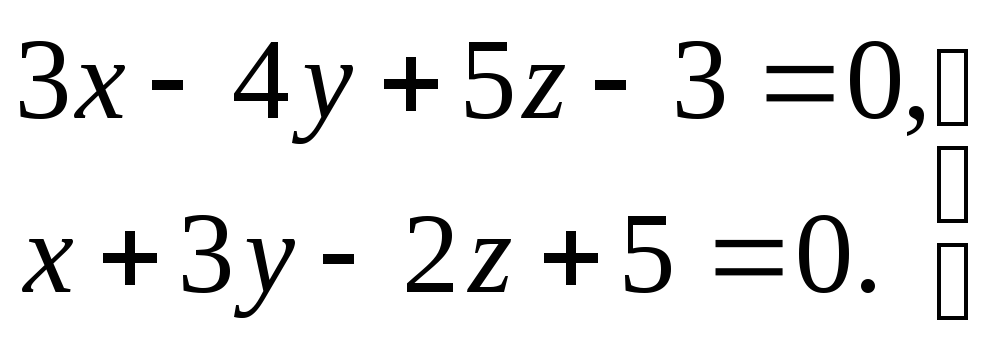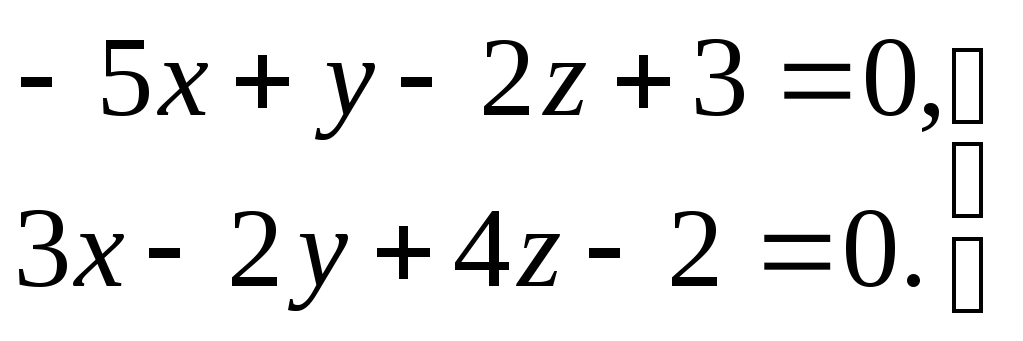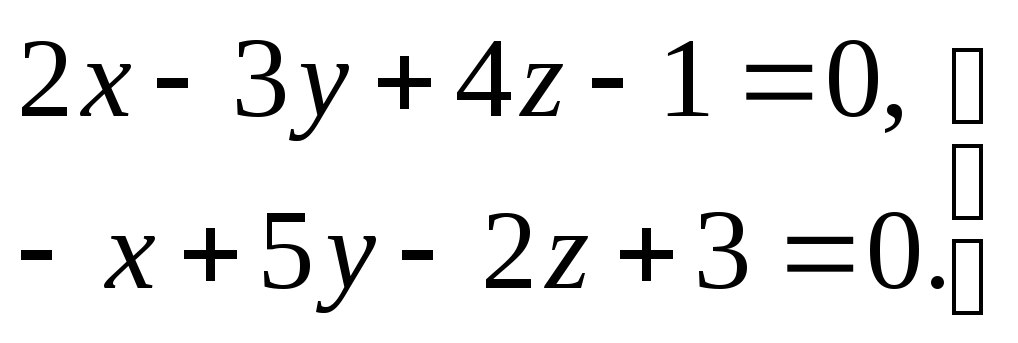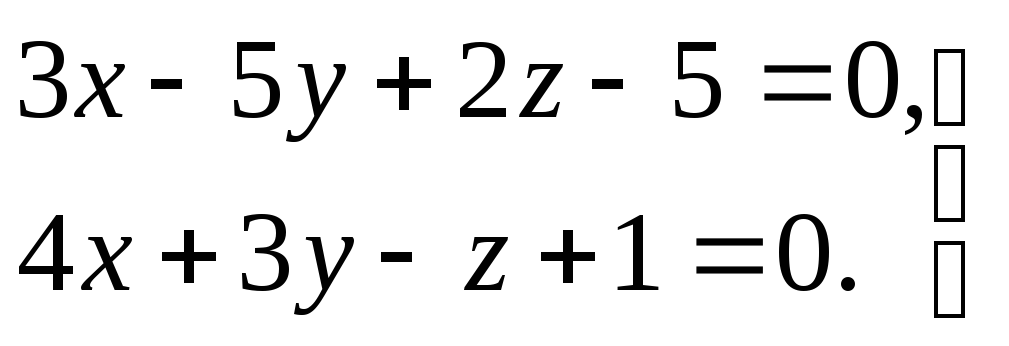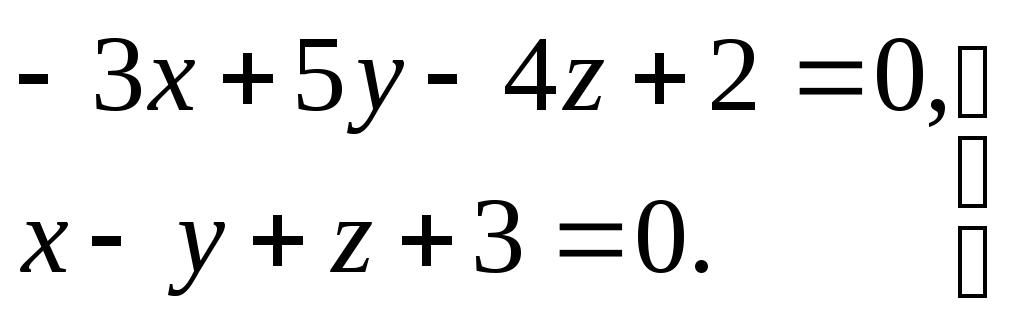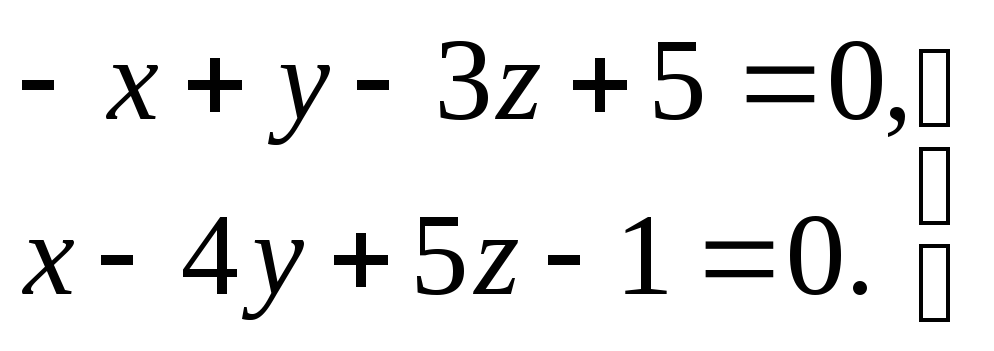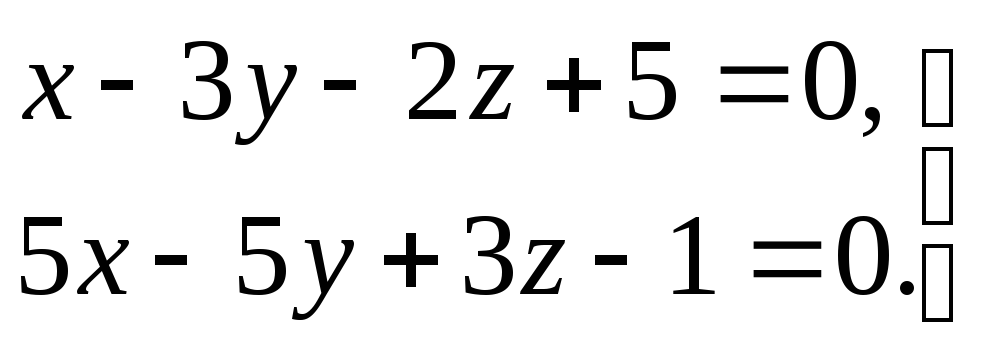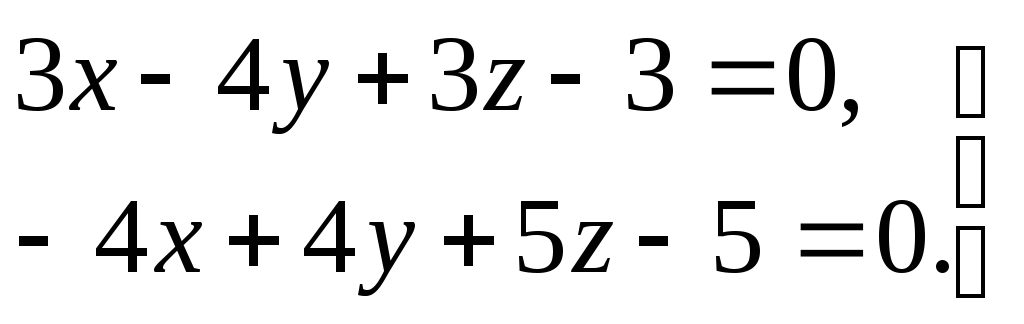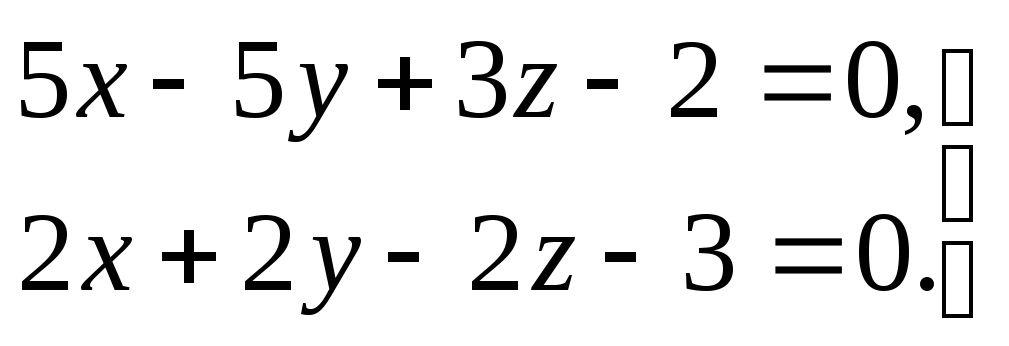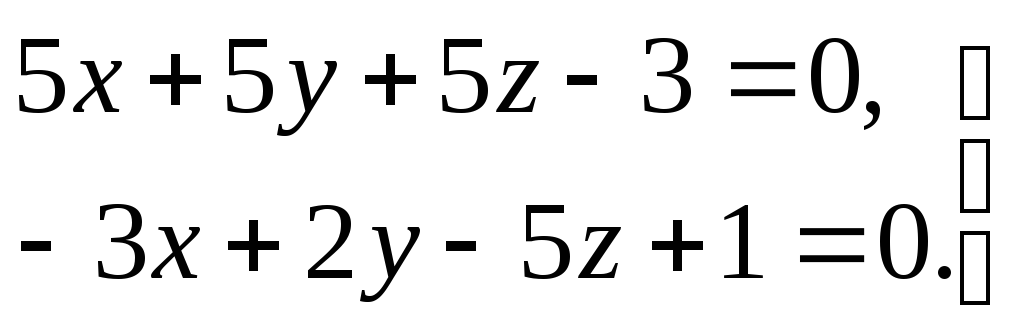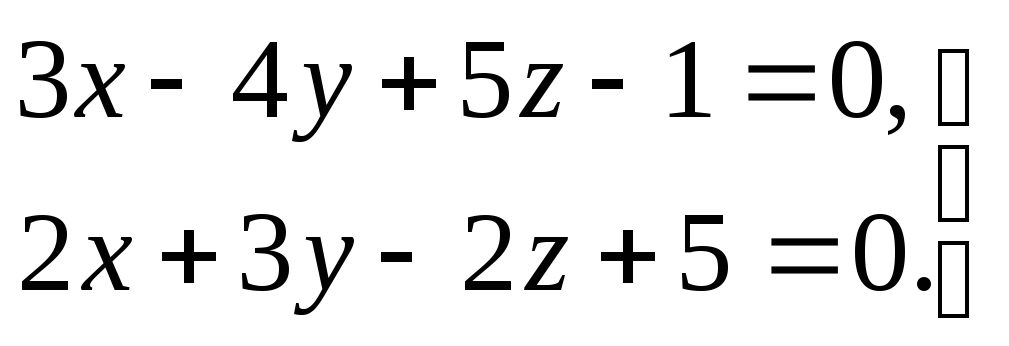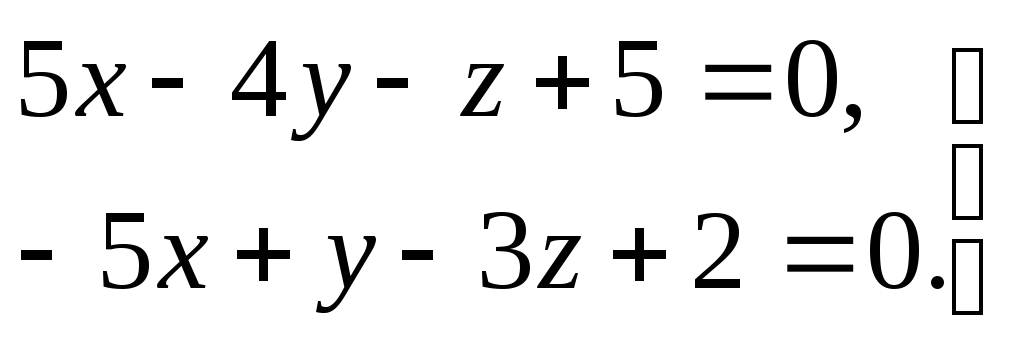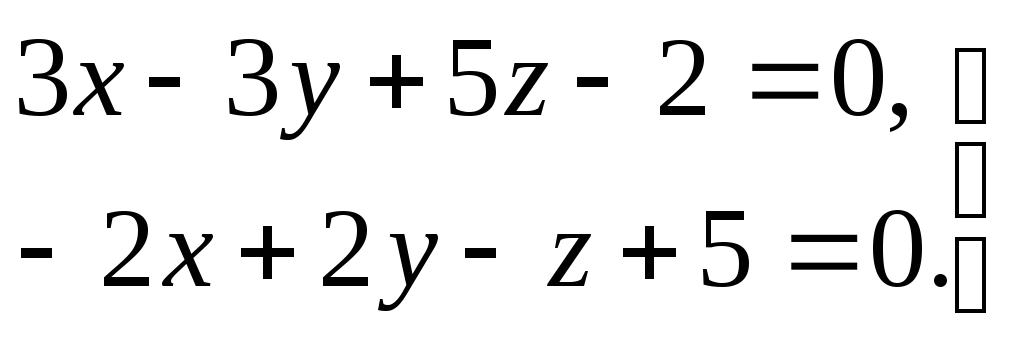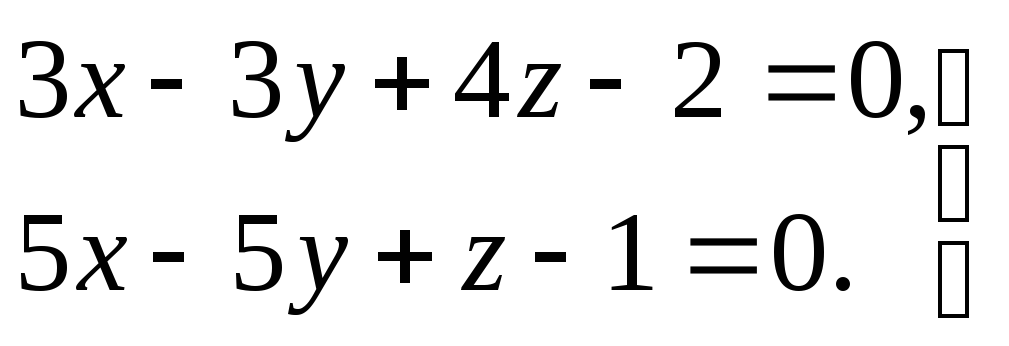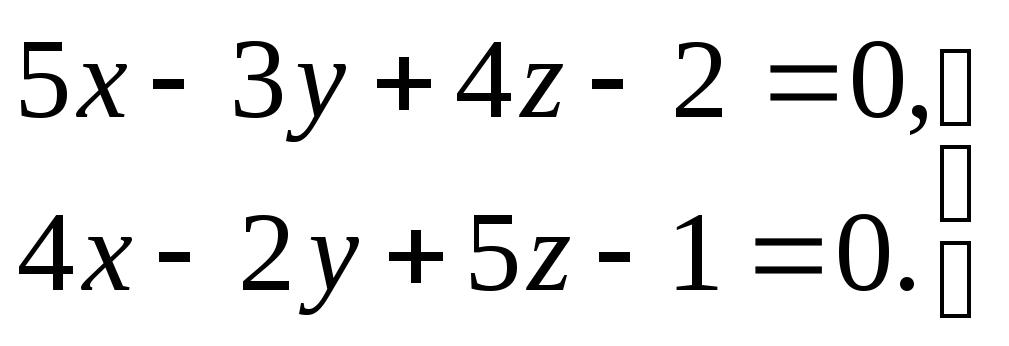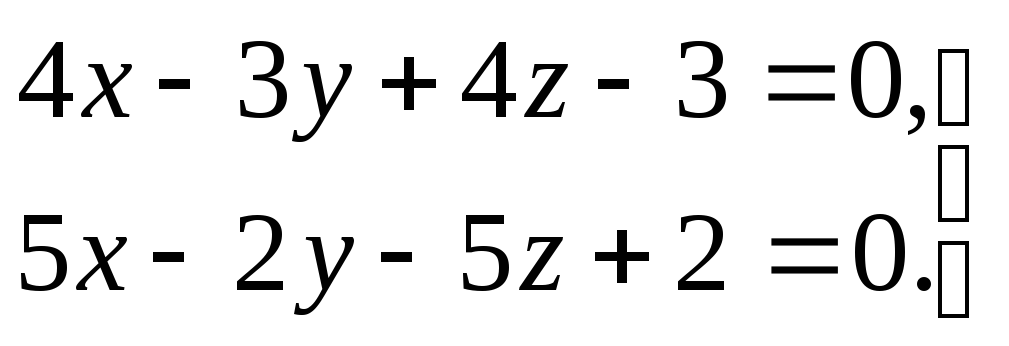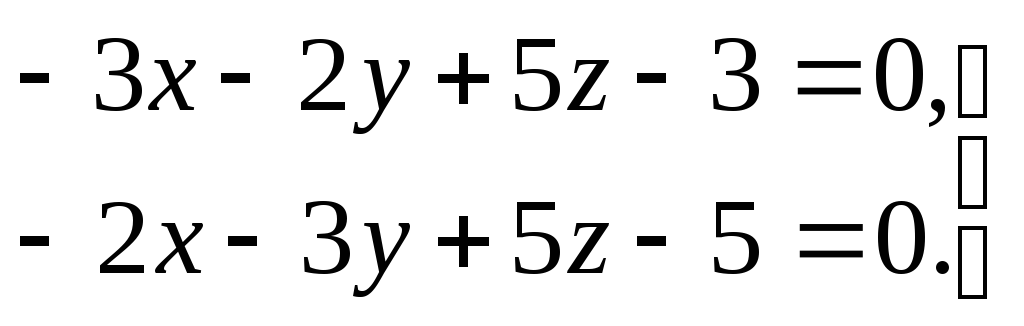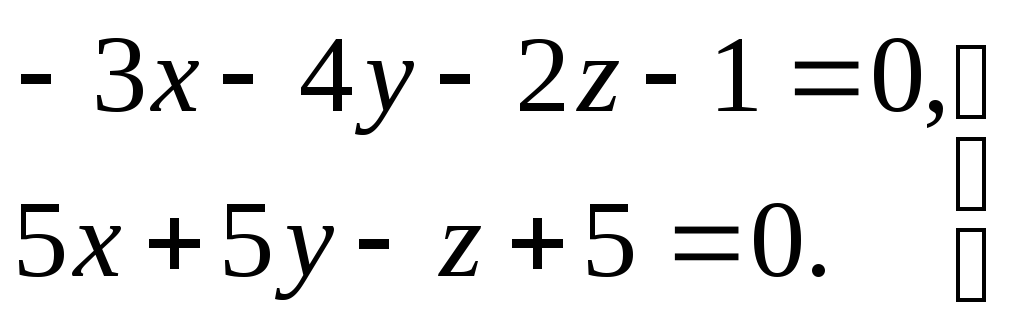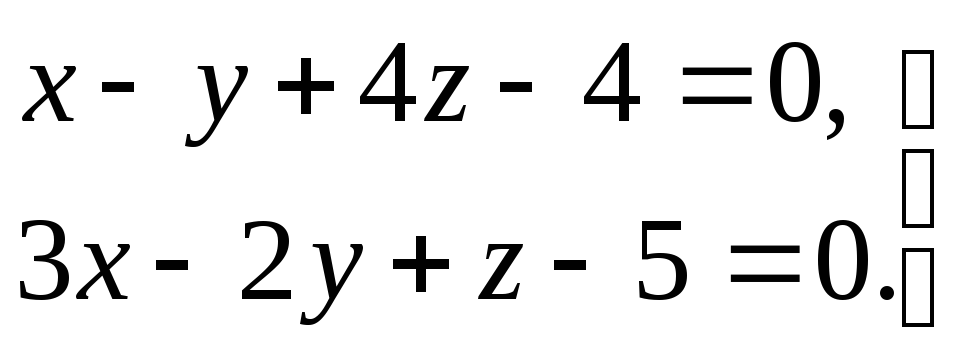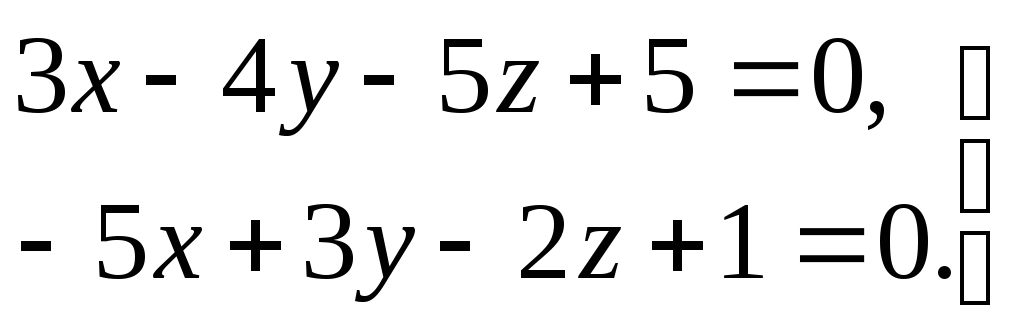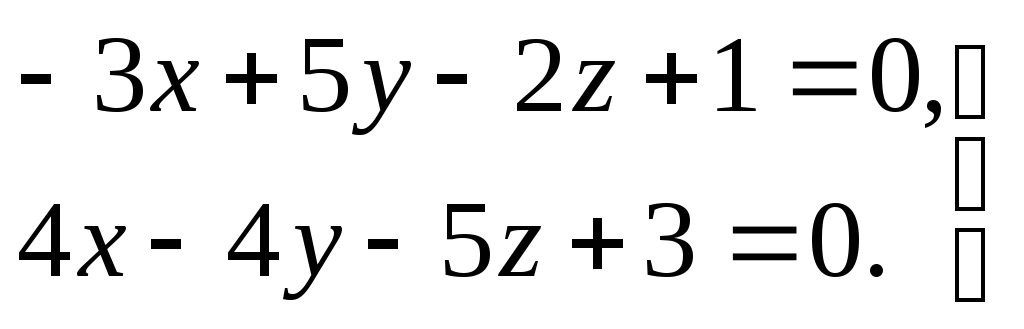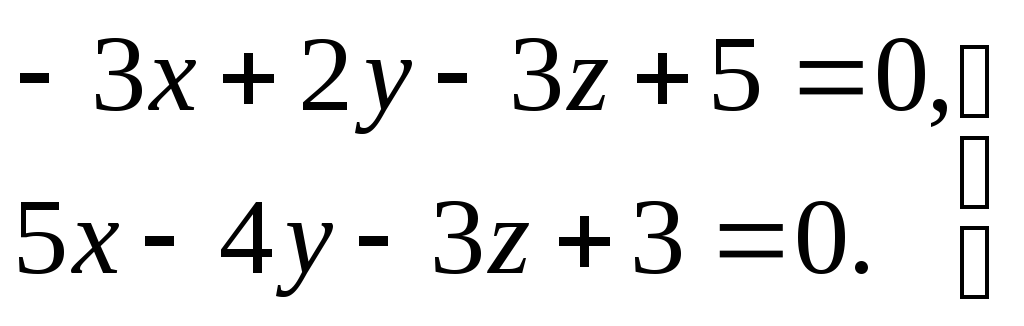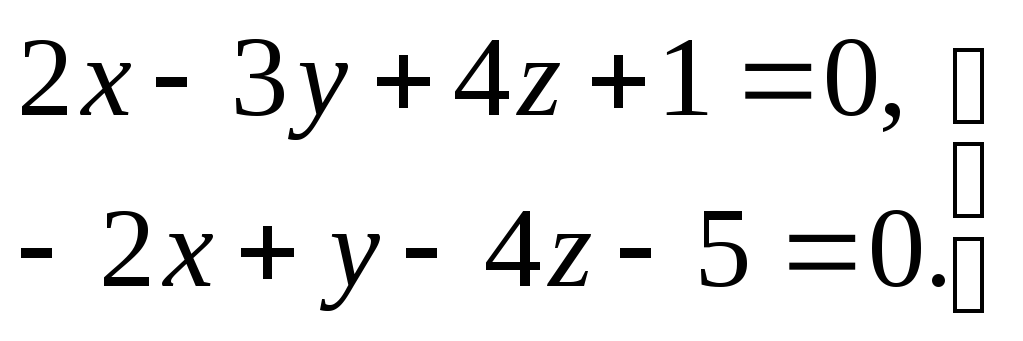- •СамарсКий государственНый университет путей сообщения
- •Содержание
- •Аналитическая геометрия
- •I. Прямые и плоскости
- •1. Плоскость
- •Задание 1
- •Задание 2
- •Задание 3
- •2. Прямая в пространстве. Прямая и плоскость
- •Задание 4
- •Задание 5
- •Задание 6
- •3. Прямая на плоскости
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Дополнительные задания
- •1 Вариант
- •2 Вариант
- •3 Вариант
- •4 Вариант
- •5 Вариант
- •6 Вариант
- •7 Вариант
- •8 Вариант
- •9 Вариант
- •10 Вариант
- •11 Вариант
- •12 Вариант
- •13 Вариант
- •14 Вариант
- •15 Вариант
- •16 Вариант
- •17 Вариант
- •18 Вариант
- •19 Вариант
- •20 Вариант
- •21 Вариант
- •22 Вариант
- •23 Вариант
- •24 Вариант
- •25 Вариант
- •26 Вариант
- •II Линии и поверхности второго порядка
- •1. Окружность и сфера
- •2. Эллипс и эллипсоид
- •3. Гипербола и гиперболоиды
- •4. Парабола и параболоиды
- •Задание 11
- •Задание 12
- •Задание 13
- •5. Цилиндры второго порядка. Конус второго порядка
- •6. Поверхности вращения
- •Задание 14
- •Задание 15
- •III. Линии, заданные уравнениями в полярных координатах и параметрическими уравнениями
- •1. Полярные координаты точки и уравнение линии в полярных координатах
- •Задание 16
- •Задание 17
- •Задание 18
- •2. Параметрические уравнения линии
- •Задание 19
2. Прямая в пространстве. Прямая и плоскость
Определение. Прямую в пространстве определим как совокупность точек, общих для двух пересекающихся плоскостей.
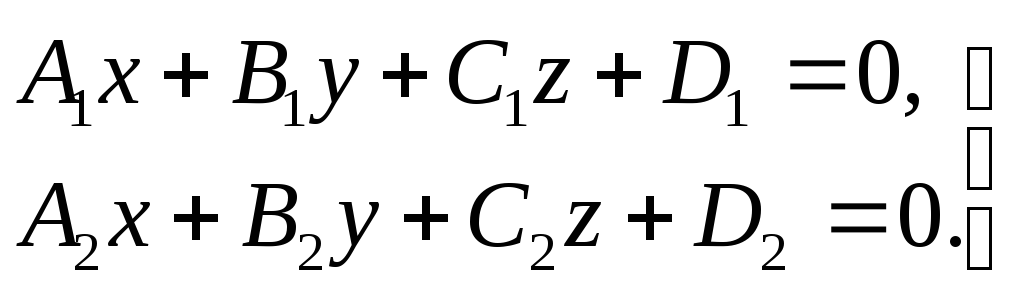 (2.1)
(2.1)
где
![]() ,
,
![]() нормальные векторы этих плоскостей,
причем
нормальные векторы этих плоскостей,
причем
![]() непараллельно
непараллельно
![]() .
Уравнение (2.1) называется общими
уравнениями прямой
в пространстве. Заметим, что направляющий
вектор
.
Уравнение (2.1) называется общими
уравнениями прямой
в пространстве. Заметим, что направляющий
вектор
![]() прямой определяется по формуле
прямой определяется по формуле
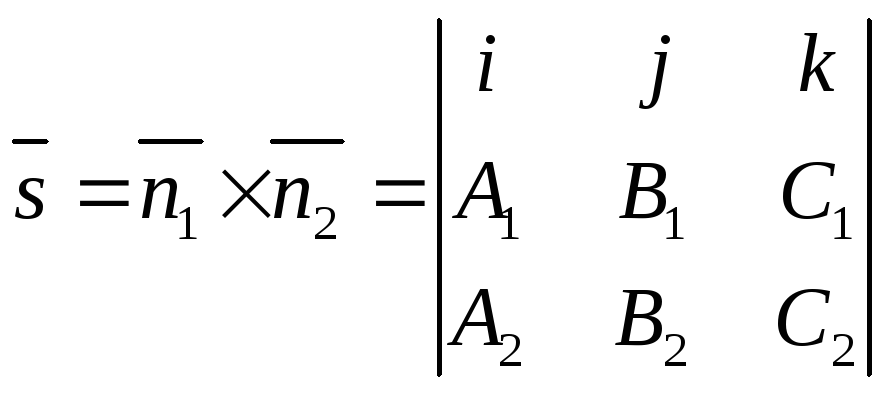
В зависимости от способа задания существует несколько видов уравнений прямой в пространстве (см. таблицу)
Таблица 2.
|
Способ задания прямой в пространстве и заданные параметры |
Вид уравнения прямой в пространстве и его название |
|
1.
Прямая задана точкой
|
Параметрические
уравнения прямой
|
|
Канонические
уравнения прямой
|
|
|
2.
Прямая задана двумя точками
|
Уравнения прямой, проходящей через 2-е точки
|
Основные задачи
1.
Угол между
прямыми
![]() и
и
![]() можно рассматривать, как угол между их
направляющими векторами
можно рассматривать, как угол между их
направляющими векторами
![]() и
и
![]()
![]() (2.5)
(2.5)
Условие
параллельности 2-х прямых:
![]() .
.
Условие
перпендикулярности 2-х прямых:
![]() .
.
2.
Расстояние
![]() от т.
от т.
![]() до прямой,
проходящей через т.
до прямой,
проходящей через т.
![]() в направлении вектора
в направлении вектора
![]() вычисляется по формуле:
вычисляется по формуле:
![]() (2.6)
(2.6)
3.
Рассмотрим случаи взаимного расположения
прямой
![]() и плоскости
и плоскости
![]() .
Возможны три случая:
.
Возможны три случая:
а)
если
![]() то прямая пересекает плоскость. Координаты
точки пересечения можно отыскать,
подставив значение
то прямая пересекает плоскость. Координаты
точки пересечения можно отыскать,
подставив значение
![]() (2.7)
(2.7)
в канонические уравнения прямой (2.2);
б)
если
![]() ,
,
![]() ,
то прямая принадлежит плоскости;
,
то прямая принадлежит плоскости;
в)
если
![]() ,
,
![]() ,
то прямая параллельна плоскости (но не
лежит в ней).
,
то прямая параллельна плоскости (но не
лежит в ней).
4.
Угол между
прямой
![]() и плоскостью
и плоскостью
![]() определяется по формуле:
определяется по формуле:
![]() (2.8)
(2.8)
Задание 4
Составить каноническое уравнения прямых и найти координаты любых двух точек для каждой прямой
1)
прямая задана точкой
![]() и направляющим вектором
и направляющим вектором
![]() ;
;
2)
прямая задана двумя точками
![]() и
и
![]() ;
;
3) прямая задана общими уравнениями
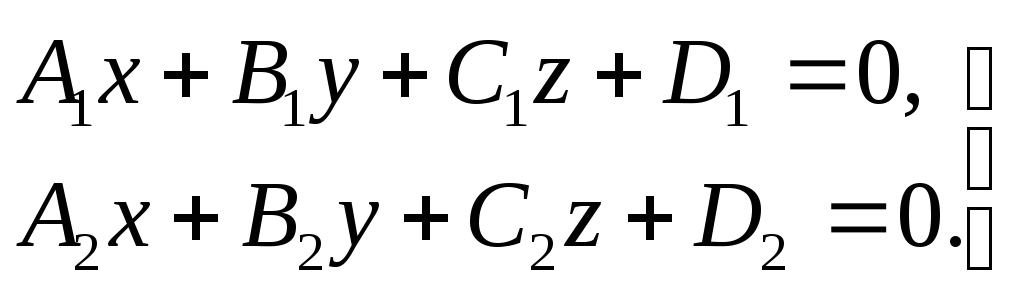 .
.
|
1
вариант.
1)
2)
3)
|
2
вариант.
1)
2)
3)
|
|
3
вариант.
1)
2)
3)
|
4
вариант.
1)
2)
3)
|
|
5
вариант.
1)
2)
3)
|
6
вариант.
1)
2)
3)
|
|
7
вариант.
1)
2)
3)
|
8
вариант.
1)
2)
3)
|
|
9
вариант.
1)
2)
3)
|
10
вариант.
1)
2)
3)
|
|
11
вариант.
1)
2)
3)
|
12
вариант.
1)
2)
3)
|
|
13
вариант.
1)
2)
3)
|
14
вариант.
1)
2)
3)
|
|
15
вариант.
1)
2)
3)
|
16
вариант.
1)
2)
3)
|
|
17
вариант.
1)
2)
3)
|
18
вариант.
1)
2)
3)
|
|
19
вариант.
1)
2)
3)
|
20
вариант.
1)
2)
3)
|
|
21
вариант.
1)
2)
3)
|
22
вариант.
1)
2)
3)
|
|
23
вариант.
1)
2)
3)
|
24
вариант.
1)
2)
3)
|
|
25
вариант.
1)
2)
3)
|
26
вариант.
1)
2)
3)
|
|
27
вариант.
1)
2)
3)
|
28
вариант.
1)
2)
3)
|
|
29
вариант.
1)
2)
3)
|
30
вариант.
1)
2)
3)
|

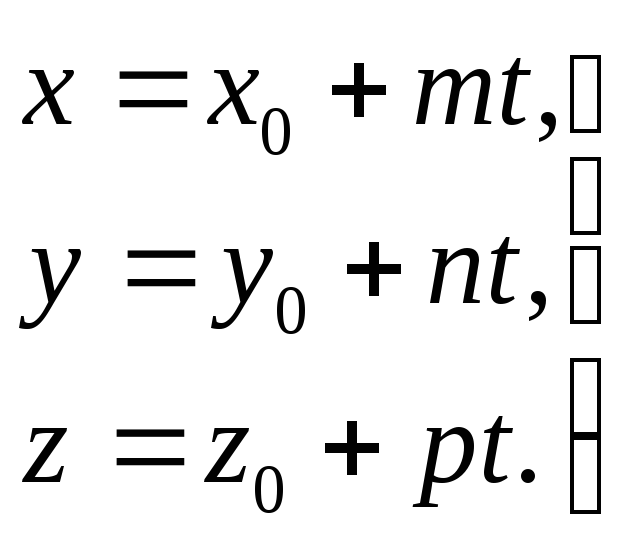 ,
где t
- параметр (2.2)
,
где t
- параметр (2.2)