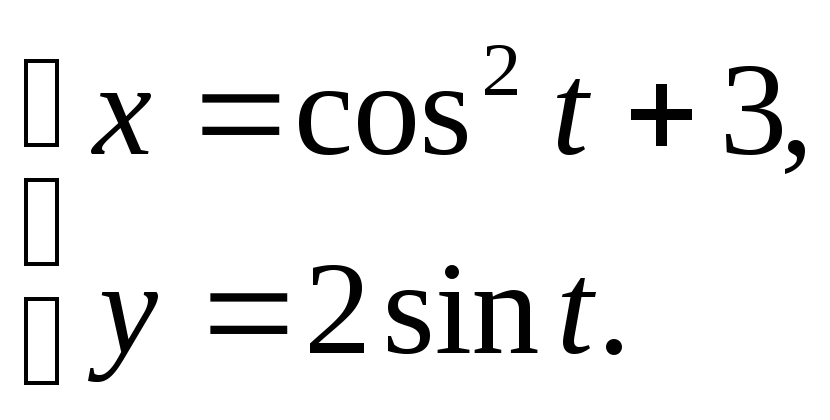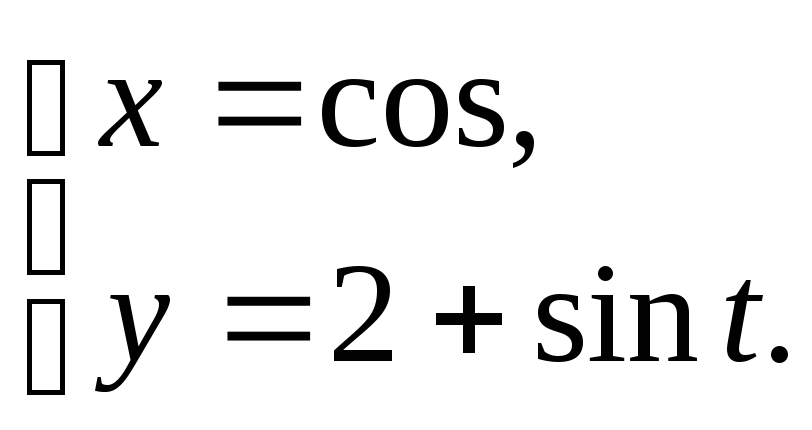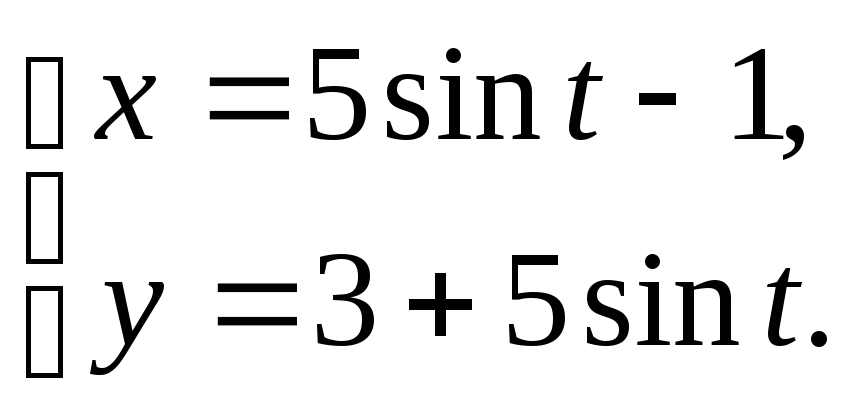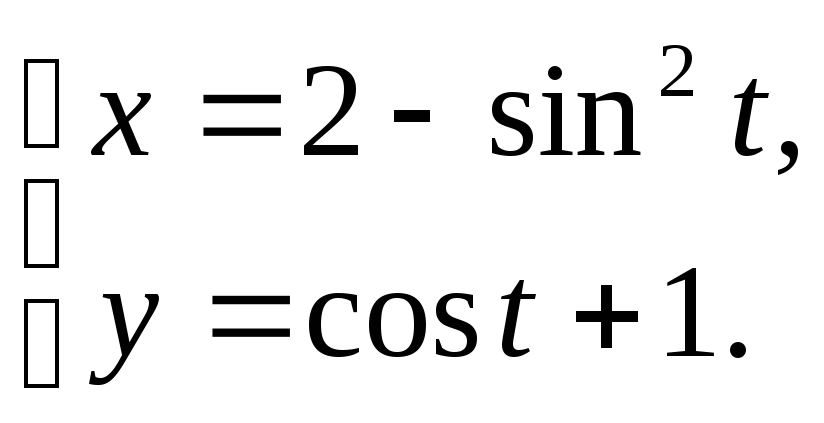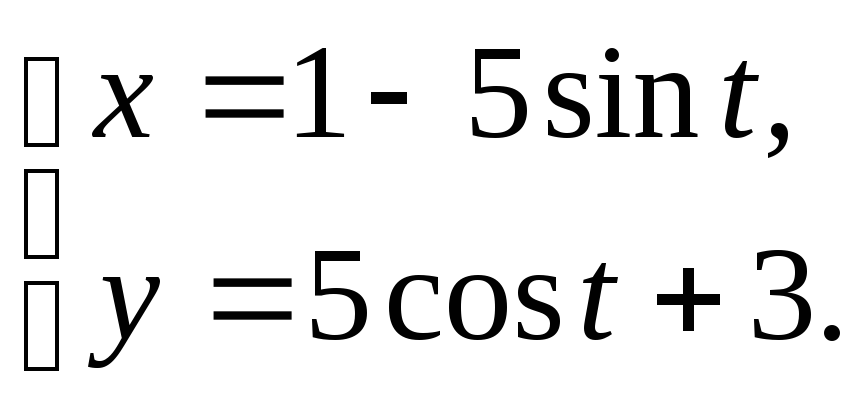- •СамарсКий государственНый университет путей сообщения
- •Содержание
- •Аналитическая геометрия
- •I. Прямые и плоскости
- •1. Плоскость
- •Задание 1
- •Задание 2
- •Задание 3
- •2. Прямая в пространстве. Прямая и плоскость
- •Задание 4
- •Задание 5
- •Задание 6
- •3. Прямая на плоскости
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Дополнительные задания
- •1 Вариант
- •2 Вариант
- •3 Вариант
- •4 Вариант
- •5 Вариант
- •6 Вариант
- •7 Вариант
- •8 Вариант
- •9 Вариант
- •10 Вариант
- •11 Вариант
- •12 Вариант
- •13 Вариант
- •14 Вариант
- •15 Вариант
- •16 Вариант
- •17 Вариант
- •18 Вариант
- •19 Вариант
- •20 Вариант
- •21 Вариант
- •22 Вариант
- •23 Вариант
- •24 Вариант
- •25 Вариант
- •26 Вариант
- •II Линии и поверхности второго порядка
- •1. Окружность и сфера
- •2. Эллипс и эллипсоид
- •3. Гипербола и гиперболоиды
- •4. Парабола и параболоиды
- •Задание 11
- •Задание 12
- •Задание 13
- •5. Цилиндры второго порядка. Конус второго порядка
- •6. Поверхности вращения
- •Задание 14
- •Задание 15
- •III. Линии, заданные уравнениями в полярных координатах и параметрическими уравнениями
- •1. Полярные координаты точки и уравнение линии в полярных координатах
- •Задание 16
- •Задание 17
- •Задание 18
- •2. Параметрические уравнения линии
- •Задание 19
Задание 19
Построить
кривую, заданную параметрическими
уравнениями по точкам, придавая t
значения
от
![]() до
до
![]() c
шагом
c
шагом![]() .
Преобразовать уравнения к уравнениям
линии в декартовой системе координат.
Определить вид и параметры кривой.
.
Преобразовать уравнения к уравнениям
линии в декартовой системе координат.
Определить вид и параметры кривой.
|
1 |
|
2 |
|
3 |
|
|
4 |
|
5 |
|
6 |
|
|
7 |
|
8 |
|
9 |
|
|
10 |
|
11 |
|
12 |
|
|
13 |
|
14 |
|
15 |
|
|
16 |
|
17 |
|
18 |
|
|
19 |
|
20 |
|
21 |
|
|
22 |
|
23 |
|
24 |
|
|
25 |
|
26 |
|
27 |
|
|
28 |
|
29 |
|
30 |
|
Решение типового варианта
Задание
19. Построить
кривую, заданную параметрическими
уравнениями
 по
точкам, придавая t
значения
от
по
точкам, придавая t
значения
от
![]() до
до
![]() c
шагом
c
шагом![]() .
Преобразовать уравнения к уравнениям
линии в декартовой системе координат.
Определить вид и параметры кривой.
.
Преобразовать уравнения к уравнениям
линии в декартовой системе координат.
Определить вид и параметры кривой.
Решение. Для построения кривой заполним таблицу
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
0 |
–1 |
0 |
–2 |
|
|
0,309 |
0,951 |
0,927 |
–0,049 |
|
–0,309 |
–0,951 |
–0,927 |
–1,951 |
|
|
0,588 |
0,809 |
1,763 |
–0,191 |
|
–0,588 |
–0,809 |
–1,763 |
–1,809 |
|
|
0,809 |
0,588 |
2,427 |
–0,412 |
|
–0,809 |
–0,588 |
–2,427 |
–1,588 |
|
|
0,951 |
0,309 |
2,853 |
–0,691 |
|
–0,951 |
–0,309 |
–2,853 |
–1,309 |
|
|
1 |
0 |
3 |
–1 |
|
–1 |
0 |
–3 |
–1 |
|
|
0,951 |
–0,309 |
2,853 |
–1,309 |
|
–0,951 |
0,309 |
–2,853 |
–0,691 |
|
|
0,809 |
–0,588 |
2,427 |
–1,588 |
|
–0,809 |
0,588 |
–2,427 |
–0,412 |
|
|
0,588 |
–0,809 |
1,763 |
–1,809 |
|
–0,588 |
0,809 |
–1,763 |
–0,191 |
|
|
0,309 |
–0,951 |
0,927 |
–1,951 |
|
–0,309 |
0,951 |
–0,927 |
–0,049 |
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
Используя данные таблицы, построим кривую
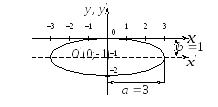
Исключим
из параметрических уравнений параметр
![]() и получим уравнение, содержащее только
и получим уравнение, содержащее только
![]() и
и
![]() .
Возводя в квадрат параметрические
уравнения и складывая, находим
.
Возводя в квадрат параметрические
уравнения и складывая, находим
![]()
![]()
![]()
![]() (*)
(*)
Выразим
![]() из второго уравнения параметрически
заданной линии
из второго уравнения параметрически
заданной линии
![]()
и подставим в (*)
![]()
Произведя необходимые преобразования, получим
![]()
![]()
![]()
![]()
![]() .
.
Получаем
уравнение эллипса с центром в точке
![]() и полуосями
и полуосями
![]() ,
,
![]() ,
что соответствует рисунку.
,
что соответствует рисунку.