Задание 13

Привести к каноническому виду уравнение кривой второго порядка , определить тип линии и построить эту кривую (таблица 4).

Таблица 4

№ вар.	Коэффициенты уравнений кривой					№ вар	Коэффициенты уравнений кривой
	A	C	D	E	F		A	C	D	E	F
1	1	1	–6	10	–15	2	1	4	0	–1	–5
3	2	0	8	–1	12	4	9	4	–54	–32	109
5	4	–9	–8	–36	–68	6	4	9	–40	36	100
7	9	–26	–54	–64	–127	8	3	3	–24	12	58
9	5	1	10	–6	–6	10	1	–1	6	0	8
11	1	7	6	–28	–12	12	3	–8	–6	–24	–36
13	9	4	18	–8	–19	14	2	0	–4	–1	–4
15	9	–4	–36	–8	–4	16	4	4	–12	4	–3
17	9	5	18	–30	9	18	36	–4	–72	16	–88
19	–4	9	16	18	29	20	4	36	–16	72	–92
21	9	4	54	8	49	22	1	4	–2	56	181
23	7	–2	–42	–16	17	24	9	–4	0	24	–72
25	–1	4	–4	8	–4	26	1	1	6	–4	0
27	1	1	–4	6	0	28	1	4	4	–16	–8
27	9	–4	–36	–8	–4	30	25	9	–100	54	–44

Решение типового варианта

Задание 11.

Построить кривые и записать их уравнения.

1. Окружность а) с центром в т. и радиусом ;

б) с центром в т. и радиусом .

2. Эллипс а) с центром в т. и полуосями и ;

б) с центром в т. и полуосями и .

3. Гипербола а) с центром в т. и полуосями - действительной, -

мнимой и сопряженную с ней гиперболу;

б) с центром в т. и полуосями - действительной,

-

мнимой

4. Парабола а) с вершиной в т. , параметром , ветви которой

направлены

- вправо,

- влево,

- вверх,

- вниз;

б) с вершиной в т. и параметром , ветви направлены

вниз.

Решение.

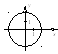
1. Уравнение окружности с центром в т. и радиусом составим по формуле (1.3)

Уравнение окружности с центром в т. и радиусом составим по формуле (1.4)

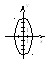
2. Уравнение эллипса с центром в т. и полуосями и согласно формуле (2.1) имеет вид

.

У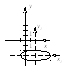равнение эллипса с центром в т. и полуосями и по формуле (2.2) имеет вид

.

3. Уравнение гиперболы с центром в т. и полуосями - действительной, - мнимой составим по формуле (3.1)

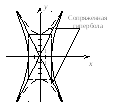
Сопряженная с ней гипербола описывается уравнением (3.2)

Уравнение гиперболы с центром в т. и полуосями и составим по формуле (3.3)

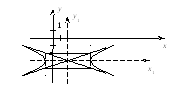
4. Уравнение параболы с вершиной в т. , параметром , ветви которой направлены вправо, согласно формуле (4.1) имеет вид

.

Уравнения подобных ей парабол с ветвями направленными влево, вверх и вниз

, , .

Уравнение параболы с вершиной в т. и параметром , ветви которой направлены вниз согласно одной из формул (4.2) имеет вид

Задание 12. Составить канонические уравнения

а) эллипса, зная что его большая полуось равна 5, а расстояние между фокусами равно 8;

б) гиперболы, проходящей через т. с эксцентриситетом ;

в) найти координаты фокуса и уравнение директрисы параболы .

Решение.

а) Т.к. расстояние между фокусами эллипса , то , по условию . Из формулы

получаем

Каноническое уравнение эллипса имеет вид (2.1)

.

б) Т.к. гипербола проходит через т. , то координаты этой точки удовлетворяют каноническому уравнению гиперболы (3.1), т.е.

. (*)

По условию , тогда , учитывая, что для гиперболы , получаем . Подставим последнее равенство в (*).

.

Окончательно получаем:

.

в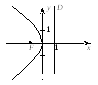) Из канонического уравнения параболы видим, что ; ; (ветви направлены влево). Тогда уравнение директрисы имеет вид: ,

фокус находится в т.

Задание 13.

Привести к каноническому виду уравнении кривой второго порядка, определить тип линии и построить эту кривую.

.

Решение.

Дополним члены, содержащие и до полных квадратов:

,

, .

Т.е. имеем гиперболу с центром в т. , действительная полуось , мнимая .