
- •СамарсКий государственНый университет путей сообщения
- •Содержание
- •Аналитическая геометрия
- •I. Прямые и плоскости
- •1. Плоскость
- •Задание 1
- •Задание 2
- •Задание 3
- •2. Прямая в пространстве. Прямая и плоскость
- •Задание 4
- •Задание 5
- •Задание 6
- •3. Прямая на плоскости
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Дополнительные задания
- •1 Вариант
- •2 Вариант
- •3 Вариант
- •4 Вариант
- •5 Вариант
- •6 Вариант
- •7 Вариант
- •8 Вариант
- •9 Вариант
- •10 Вариант
- •11 Вариант
- •12 Вариант
- •13 Вариант
- •14 Вариант
- •15 Вариант
- •16 Вариант
- •17 Вариант
- •18 Вариант
- •19 Вариант
- •20 Вариант
- •21 Вариант
- •22 Вариант
- •23 Вариант
- •24 Вариант
- •25 Вариант
- •26 Вариант
- •II Линии и поверхности второго порядка
- •1. Окружность и сфера
- •2. Эллипс и эллипсоид
- •3. Гипербола и гиперболоиды
- •4. Парабола и параболоиды
- •Задание 11
- •Задание 12
- •Задание 13
- •5. Цилиндры второго порядка. Конус второго порядка
- •6. Поверхности вращения
- •Задание 14
- •Задание 15
- •III. Линии, заданные уравнениями в полярных координатах и параметрическими уравнениями
- •1. Полярные координаты точки и уравнение линии в полярных координатах
- •Задание 16
- •Задание 17
- •Задание 18
- •2. Параметрические уравнения линии
- •Задание 19
14 Вариант
1.
Найти угол наклона прямой, проходящей
через точки
![]() и
и
![]() к плоскости
к плоскости
![]() .
.
2.
Записать уравнения прямой в канонической
форме

3. Найти уравнение плоскости, проходящей через точки М1(1;1;1) и М2(–1;1;–1), параллельно вектору АВ, где А(5;–2;3), В(6;1;0).
4. Даны уравнения стороны АВ треугольника ABC 4х + у = 12, его высот ВН 5х–4у = 12 и AM х + у = 6. Найти уравнения двух других сторон треугольника ABC.
5. Даны координаты вершин пирамиды A1(l;1;1), А2(3 4;0), А3(–1:5;6), А4(4;0;5).
Найти: a) длину ребра А2А3;
b) угол между ребрами A1A2 и A1A4;
c) проекцию вектора A1A2 на вектор A1A4.
15 Вариант
1.
Найти уравнение прямой, проходящей
через точку пересечения прямых
![]() ,
,
![]() и отсекающей на оси абсцисс отрезок,
равный 3.
и отсекающей на оси абсцисс отрезок,
равный 3.
2. Даны две точки А(1;3;–2) и В(7;–4;–4). Через точку В провести плоскость, перпендикулярную к отрезку АВ.
3. Составить уравнение плоскости, проходящей через три точки M(0;0;2), N(3;0;5), Р(4;1;2).
4. Найти направляющие косинусы прямой и записать уравнения прямой в каноническом виде

5.
Найти проекции векторов
![]() ={2;1;3}
и
={2;1;3}
и
![]() =
{l;2;
–l} на
вектор
=
{l;2;
–l} на
вектор
![]() .
.
16 Вариант
1. Найти точку пересечения прямой и плоскости и угол между ними
![]() ,
,
![]()
2.
Из точки
![]() провести прямую, перпендикулярную
плоскости, проходящей через точку
провести прямую, перпендикулярную
плоскости, проходящей через точку
![]() ,
,
![]() ,
,
![]() .
.
3.
Найти уравнение плоскости, проходящей
через точку
![]() перпендикулярно к плоскостям
перпендикулярно к плоскостям
![]() и
и
![]() .
.
4.
Найти расстояние
от точки А(2;–1)
до прямой, проходящей через точку
![]() и точку
и точку
![]() .
.
5.
Определить длины диагоналей параллелограмма,
построенного на векторах
![]() и
и
![]() ,
где
,
где
![]() и
и
![]() единичные векторы, угол между которыми
равен
единичные векторы, угол между которыми
равен
![]() .
.
17 Вариант
1.
Записать уравнения прямой в канонической
форме

2.
Дано
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Написать уравнение перпендикуляра к
плоскости
.
Написать уравнение перпендикуляра к
плоскости
![]() проходящего
через точку
проходящего
через точку
![]() .
.
3.
Определить направляющие косинусы
вектора перпендикулярного к плоскости
![]() .
.
4.
Даны вершины треугольника АВС:
![]() ,
,
![]() ,
,
![]() .
Написать уравнение медианы ВМ.
.
Написать уравнение медианы ВМ.
5.
На материальную точку действуют силы
![]() ,
,
![]() ,
,
![]() .
.
Найти
работу равнодействующей этих сил при
перемещении точки из положения
![]() в положении
в положении
![]() .
.
18 Вариант
1.
Доказать, что прямые взаимно перпендикулярны:
 ,
,
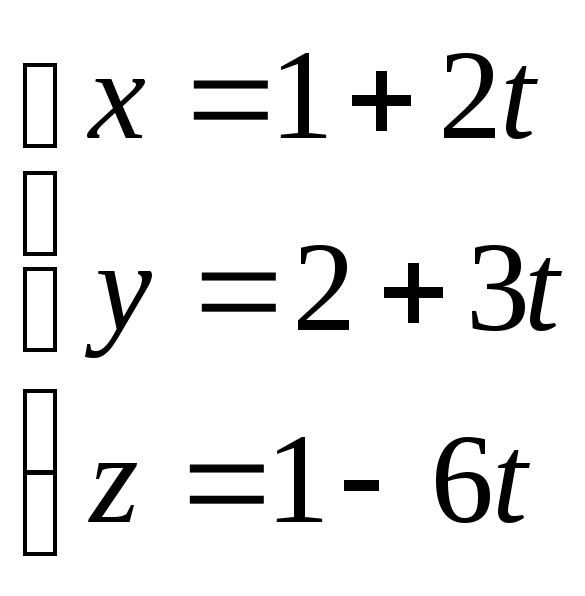 .
.
2.
Определить угол между двумя прямыми:
 ,
,
![]() .
.
3.
Из точки
![]() опустить перпендикуляр на плоскость
опустить перпендикуляр на плоскость
![]() .
.
4.
Найти проекцию точки А(1;
2; 1) на прямую
![]() .
.
5. Даны координаты вершин параллелепипеда: А(4;2;–1), В(3;0;4), С(0;0;4), D(5;–1;–3). Найти объем параллелепипеда и высоту в треугольнике ABC из точки А.
19 Вариант
1.
Точка
![]() является основанием перпендикуляра,
опущенного из начала координат на
плоскость. Найти уравнение плоскости.
является основанием перпендикуляра,
опущенного из начала координат на
плоскость. Найти уравнение плоскости.
2.
Найти угол между прямой
![]() и плоскостью, проходящей через точки
и плоскостью, проходящей через точки
![]() ,
,
![]() ,
,
![]() .
.
3. Написать уравнения прямой, проходящей через точку М(2;2;1) параллельно прямой
 .
.
4.
Записать уравнение прямой, проходящей
через точку
![]() перпендикулярно к прямой ВС,
если
перпендикулярно к прямой ВС,
если
![]() ,
,
![]() .
.
5.
Проверить, что четыре точки
![]() ,
,
![]() ,
,
![]() ,
,
![]() лежат в одной плоскости.
лежат в одной плоскости.
20 Вариант
1.
Составить уравнение прямой, проходящей
через точку
![]() параллельно прямой
параллельно прямой
![]() .
Найти расстояние между прямыми.
.
Найти расстояние между прямыми.
2.
При каких значениях п
и А
прямая
![]() перпендикулярна к плоскости
перпендикулярна к плоскости
![]() .
.
3.
Известны уравнения двух сторон ромба
![]() ,
,
![]() и уравнение одной из его диагоналей
и уравнение одной из его диагоналей
![]() .
Найти уравнение второй диагонали.
.
Найти уравнение второй диагонали.
4. Даны вершины треугольника ABC: A(4;–3), В(7;3), С(1;10). Записать уравнение высоты СH.
5. Найти объем пирамиды с вершинами в точках А(1;2;–1), B(l;2;l), C(4;l;l), D(–l;3;2).
