
- •СамарсКий государственНый университет путей сообщения
- •Содержание
- •Аналитическая геометрия
- •I. Прямые и плоскости
- •1. Плоскость
- •Задание 1
- •Задание 2
- •Задание 3
- •2. Прямая в пространстве. Прямая и плоскость
- •Задание 4
- •Задание 5
- •Задание 6
- •3. Прямая на плоскости
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Дополнительные задания
- •1 Вариант
- •2 Вариант
- •3 Вариант
- •4 Вариант
- •5 Вариант
- •6 Вариант
- •7 Вариант
- •8 Вариант
- •9 Вариант
- •10 Вариант
- •11 Вариант
- •12 Вариант
- •13 Вариант
- •14 Вариант
- •15 Вариант
- •16 Вариант
- •17 Вариант
- •18 Вариант
- •19 Вариант
- •20 Вариант
- •21 Вариант
- •22 Вариант
- •23 Вариант
- •24 Вариант
- •25 Вариант
- •26 Вариант
- •II Линии и поверхности второго порядка
- •1. Окружность и сфера
- •2. Эллипс и эллипсоид
- •3. Гипербола и гиперболоиды
- •4. Парабола и параболоиды
- •Задание 11
- •Задание 12
- •Задание 13
- •5. Цилиндры второго порядка. Конус второго порядка
- •6. Поверхности вращения
- •Задание 14
- •Задание 15
- •III. Линии, заданные уравнениями в полярных координатах и параметрическими уравнениями
- •1. Полярные координаты точки и уравнение линии в полярных координатах
- •Задание 16
- •Задание 17
- •Задание 18
- •2. Параметрические уравнения линии
- •Задание 19
8 Вариант
1.
Составить канонические уравнения
прямой, проходящей через точку
![]() перпендикулярно
плоскости, проходящей через точки
А1(3;0;0),
А2(0;2;3),
А3(1;4;1).
перпендикулярно
плоскости, проходящей через точки
А1(3;0;0),
А2(0;2;3),
А3(1;4;1).
2.
Найти уравнение плоскости, проходящей
через точки
![]() ,
,
![]() и перпендикулярной плоскости
и перпендикулярной плоскости
![]() .
.
3.
Доказать, что прямая
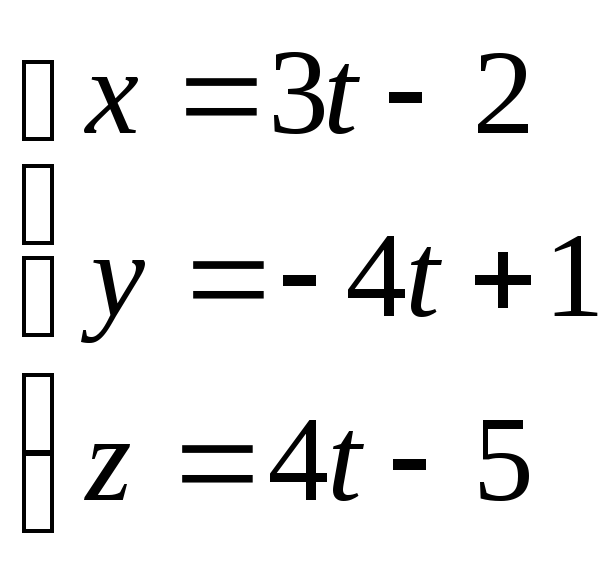 параллельна плоскости
параллельна плоскости
![]() .
.
4.
Даны вершины треугольника АВС:
![]() ,
,
![]() ,
,
![]() .
Найти точку пересечения медианы AM
и высоты СН.
.
Найти точку пересечения медианы AM
и высоты СН.
5.
Вычислить объем и высоту параллелепипеда,
построенного на трех данных векторах:
![]() ,
,
![]() ,
,
![]() .
.
9 Вариант
1. Найти угол между плоскостью х + у = 0 и плоскостью, проходящей через три точки: М1(1;3;0), М2(4;–1;2), М3(3;0;1).
2. Даны две вершины треугольника ABC: A(–6;2), В(2;–2) и точка пересечения его высот Н(1;2). Найти координаты точки М пересечения стороны АС и высоты ВН.
3.
Написать уравнение прямой, проходящей
через точку М0(2;–3;–4)
параллельно прямой
 .
.
4.
Показать, что прямые
![]() и
и
 перпендикулярны.
перпендикулярны.
5.
Вычислить диагонали и площадь
параллелограмма, построенного на
векторах
![]() и
и
![]() .
.
10 Вариант
1.
При каком
![]() пересекаются прямые
пересекаются прямые
 и
и
![]() .
.
2.
Найти
расстояние от точки А(–3;
3) до прямой
![]() .
.
3. Составить уравнение плоскости, проходящей через точку М(–2;7;3) параллельно плоскости x – 4y + 5z – l = 0.
4. Даны вершины треугольника ABC: A(7; 0), В(4; 1), С(–4; –8). Написать уравнение медианы ВМ.
5. Даны координаты вершин пирамиды A1(3;1;–2), А2(1;–2;1), А3(–2;1;0), А4(2;2;5). Найти объем пирамиды и высоту, опущенную из вершины А3.
11 Вариант
1.
Составить канонические уравнения прямой
проходящей через начало координат и
параллельно прямой
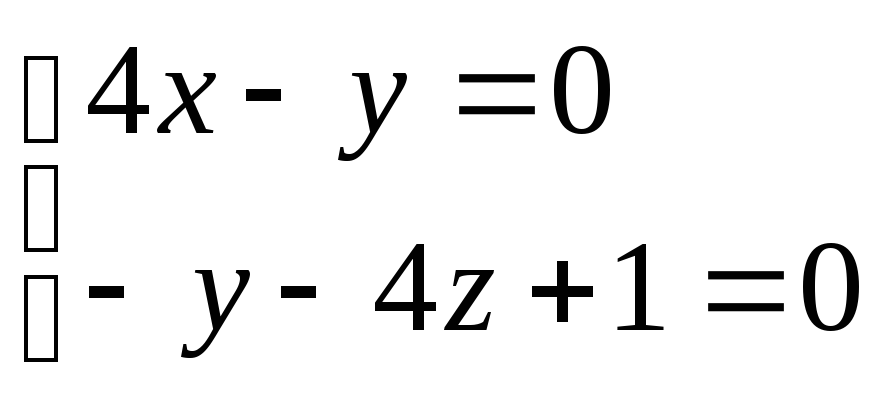 .
.
2.
Найти угол между прямой
![]() и плоскостью
и плоскостью
![]() .
.
3. Составить параметрические уравнения прямой, проходящей через точку А4(1;1;0) и перпендикулярно плоскости A1A2A3, проходящей через три заданных точки: А1(3;0;5); А2(0;0;2), А3(4;1;2).
4.
Найти расстояние от точки Р(1;2;3)
до прямой
![]() .
.
5. Даны вершины треугольника ABC: A(l;–1;2), В(5;–6;2), С(1;3;1). Вычислить длину его высоты, опущенной из вершины В на сторону АС.
12 Вариант
1.
Определить угол между прямой
 и плоскостью
х
–
2у
+ z
+ 4 = 0.
и плоскостью
х
–
2у
+ z
+ 4 = 0.
2.
Найти расстояние от точки
![]() до прямой
до прямой
![]() .
.
3. Составить уравнение плоскости, проходящей через точки M1(–1; 3;2), М2(–1;3; –1) и перпендикулярно к плоскости 3х + 4у + 12z – 1 = 0.
4. Даны вершины треугольника АВС: А(–2;–6), В(–3;5), С(4;0). Найти точку пересечения медианы АМ и высоты СH.
5.
Установить, компланарны ли векторы :
![]() ,
,
![]() ,
,
![]() .
.
13 Вариант
1.
Через точку пересечения прямых
![]() и
и
![]() провести прямую параллельную оси Oy.
провести прямую параллельную оси Oy.
2.
Установить, плоскости
![]() ;
;
![]() ;
;
![]() имеют единственную общую точку, и найти
ее координаты.
имеют единственную общую точку, и найти
ее координаты.
3.
Найти угол между прямыми
 и
и
![]() .
.
4. Составить канонические уравнения прямой, проходящей через точку А4(1;1;0) перпендикулярно плоскости, проходящей через точки А1(3;0;5), А2(0;0;2), А3(4;1;2).
5.
Даны три силы
![]() ,
,
![]() ,
,
![]() ,
приложенные к одной точке. Вычислить,
какую работу производит равнодействующая
этих сил, когда точка ее приложения,
двигаясь прямолинейно, перемещается
из положения С(5;3;–7)
в положение В(4;–1;4).
,
приложенные к одной точке. Вычислить,
какую работу производит равнодействующая
этих сил, когда точка ее приложения,
двигаясь прямолинейно, перемещается
из положения С(5;3;–7)
в положение В(4;–1;4).
