Показатели вариации

Размах вариации, или размах колебания ( R ) R = X_max – X_min. (7.1)

среднее линейное отклонение ()

для несгруппированных (простое) (7.2)
для сгруппированных данных (взвешенное) (7.3)
показатель дисперсии (2) для несгруппированных , (7.4) сгруппированных данных , (7.5)

Формула центрального момента второго порядка:

. (7.7)

Среднее квадратическое отклонение

. (7.8)

Коэффициент вариации является наиболее распространённым показателем колеблемости, используемым для оценки типичности средних величин.

. (7.11)

Общая дисперсия характеризует вариацию признака, которая зависит от всех усилий в данной совокупности.

, (8.21)

где  общая, для всей изучаемой совокупности. – численность отдельных групп.

Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризует межгрупповая дисперсия, которая является мерой колеблемости частных (групповых) средних по группам вокруг общей средней х ₀, и которая отражает вариацию изучаемого признака, возникающую под влиянием признака-фактора, положенного в основу группировки.

, (8.22)

где х_i – средняя по отдельным группам, х₀ – общая средняя по совокупности единиц;

f_i – число единиц в отдельной группе.

Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия .

. (8.23)

По совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из внутригрупповых дисперсий. Она характеризует случайную вариацию в каждой отдельной группе и не зависит от условия (признака-фактора), положенного в основу группировки.

, (8.24) или

, (8.25)

Между общей дисперсией (), средней из внутригрупповых дисперсий () и межгрупповой ( ²) дисперсиями существует соотношение, определяемое как правило сложения дисперсий. . (8.26)

Это правило (закон) сложения вариаций (дисперсий) имеет большую практическую значимость, т.к. позволяет выявить зависимость результатов от определяющих факторов соотношением межгрупповой и общей дисперсии (коэффициент детерминации). (100) определяет влияние других факторов.

. (8.27)

Дисперсия альтернативного признака

Наряду с показателями вариации количественного признака определяются показатели вариации альтернативного признака.

Альтернативными являются признаки, которыми обладают одни единицы изучаемой совокупности и не обладают другие. Т.е. в данном случае это два взаимоисключающих варианта. Переменная принимает значение 1, если обследуемая единица обладает данным признаком, а значение 0 - когда не обладает им. Пусть общее число единиц совокупности равно n, число единиц, обладающих данным признаком – f, тогда число единиц, необладающих данным признаком, будет равно (n f). Тогда распределение по качественному признаку:

Значение переменной	Частота повторений	p + q = 1.
1 0	f n – f	2 не может быть больше 0,25.
Итого	n	. (8.31)

Статистическое изучение взаимосвязи социально-экономических явлений

Таблица 8.1 - Количественные критерии оценки и тесноты связи

Величина коэффициента корреляции	Теснота связи
	практически отсутствует
	слабая
	умеренная
	сильная

По направлению выделяют связь прямую и обратную.

По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные. Если статистическая связь между явлениями может быть приблизительно выражена уравнением прямой линии, то её называют линейной связью вида

у_х = а₀ + а₁х . (8.1)

Если же связь может быть выражена уравнением какой-либо кривой линии, например:

параболы  = а₀ + а₁х + а₂ , (8.2)

гиперболы  у_х = а₀ + а₁ / х и т.д., (8.3)

Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид

na₀+a₁x = y,

a₀x+a₁x²=xy, (8.5)

где n – объём исследуемой совокупности.

Система нормальных уравнений для нахождения параметров уравнении параболы второго порядка методом наименьших квадратов имеет следующий вид

na₀+a₁x + а₂x² = y,

a₀x+a₁x² + а₂x³ = xy, (8.7)

а₀x²+ a₁x³ + а₂x⁴ = x ²y,

Линейный коэффициент корреляции характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.

. (8.10)

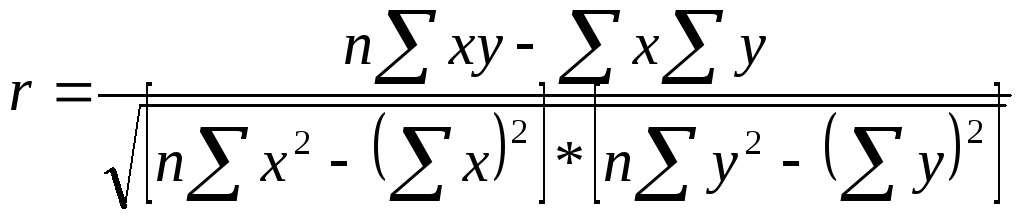. (8.11)

Между линейным коэффициентом корреляции и коэффициентом регрессии существует определённая зависимость, выражаемая формулой

, (8.12)

Таблица 8.2 Оценка линейного коэффициента корреляции

Значение линейного коэффициента связи	Характер связи	Интерпретация связи
r = 0	отсутствует	
0 < r < 1	прямая	с увеличением х увеличивается у
-1 < r < 0	обратная	с увеличением х уменьшается у и наоборот
r = 1	функциональная	каждому значению факторного признака строго соответствует одно значение результативного признака

Эмпирическое корреляционное отношение

, (8.13)

где – средняя из частных (групповых) дисперсий;  - корреляционное отношение;

 ² – общая дисперсия;  ² – межгрупповая дисперсия (дисперсия групповых средних).

Все эти дисперсии есть дисперсии результативного признака.

Теоретическое корреляционное отношение определяется

, (8.14)

где  ² – дисперсия выравненных значений результативного признака, то есть рассчитанных по уравнению регрессии;

 ² – дисперсия эмпирических (фактических) значений результативного признака.

Корреляционное отношение изменяется в пределах от 0 до 1 (0    1)

Для измерения тесноты связи при множественной корреляционной зависимости, то есть при исследовании трёх и более признаков одновременно, вычисляются множественный и частные коэффициенты корреляции.

Множественный коэффициент корреляции , (8.15)

где r _ух - парные коэффициенты корреляции между признаками.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: 0  R  1.

В случае зависимости у от двух факторных признаков х₁ и х₂ коэффициенты частной корреляции имеют вид

, (8.16)

где r – парные коэффициенты корреляции между указанными в индексе переменными. В первом случае исключено влияние факторного признака х₂, во втором – х₁.

, (8.17)

Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый. Знаки коэффициентов регрессии говорят о характере влияния на результативный признак. Если факторный признак имеет знак плюс, то с увеличением данного фактора результативный признак возрастает, если факторный признак имеет знак минус, то с его увеличением результативный признак уменьшается.

Если экономическая теория подсказывает, что факторный признак должен иметь положительное значение, а он имеет знак минус, то необходимо проверить расчёты параметров уравнения регрессии. Такое явление чаще всего бывает в силу допущенных ошибок при решении. Однако следует иметь в виду, что, когда рассматривается совокупное влияние факторов, то в силу наличия взаимосвязей между ними характер их влияния может меняться. С целью расширения возможностей экономического анализа используются частные коэффициенты эластичности, определяемые по формуле

, (8.18)

где – среднее значение соответствующего факторного признака;

у – среднее значение результативного признака;

а₁ – коэффициент регрессии при соответствующем факторном признаке.

Коэффициент эластичности показывает: на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1 %.

Частный коэффициент детерминации:

, (8.19)

где – парный коэффициент корреляции между результативным и i - м факторным признаком;

– соответствующий стандартизированный коэффициент уравнения множественной регрессии:

. (8.20)

Методы изучения связи качественных признаков

Таблица 8.3 Вспомогательная таблица для вычисления коэффициентов ассоциации и контингенции

а	b	a + b
c	d	c + d
a + c	b + d	a + b + c + d

Коэффициенты вычисляются по формулам:

а) ассоциации:	Ка=	(8.21)
б ) контингенции:	Кk=	(8.22)

Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтверждённой, если К_а  0,5 или К_k  0,3.

Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициента взаимной сопряжённости Пирсона-Чупрова. Этот коэффициент вычисляется по следующей формуле:

,	(8.23)
,	(8.24)

где ² – показатель взаимной сопряжённости;  - определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки.

Вычитая из суммы «1», получим величину ²:

² = , (8.25)

где К₁ – число значений (групп) первого признака;

К₂ – число значений (групп) второго признака.

Чем ближе величина К_n и К_ч к 1, тем теснее связь.

Таблица 8.4 Вспомогательная таблица для расчёта коэффициента взаимной сопряжённости

х	у			Всего
	I	II	III
I II III			nxy	nx nx nx
Итого	ny	ny	ny	n

1+² = . (8.26)

Особое значение для оценки связи имеет биссериальный коэффициент корреляции, который даёт возможность оценить связь между качественным альтернативным и качественным варьирующим признаками. Данный коэффициент вычисляется по формуле

, (8.27)

где и у₁ – средние в группах; _у – среднее квадратическое отклонение фактических значений признака от среднего уровня; p – доля первой группы; q – доля второй группы; z – табулированные (табличные) значения Z-распределения в зависимости от p.

Величина биссериального коэффициента корреляции также подтверждает величину тесноты связи между изучаемыми признаками.

Ранговые коэффициенты связи

В анализе социально-экономических явлений часто приходится прибегать к различным условным оценкам с помощью рангов, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи.

Ранг – это порядковый номер значений признака из группы признаков, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической из соответствующих номеров мест, которые определяют. Данные ранги называются связными.

Ранжирование – это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения.

Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена () и Кендалла (). Эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками.

Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается по формуле

_ху = 1 - , (8.28)

где d _i² – квадраты разности рангов; n – число наблюдений (число пар рангов).

Коэффициент Спирмена принимает любые значения в интервале [-1;1].

Ранговый коэффициент корреляции Кендалла () также может использоваться для измерения взаимосвязи между качественными и количественными признаками, характеризующими однородные объекты и ранжированные по одному принципу. Расчёт рангового коэффициента Кендалла осуществляется по формуле

 = , (8.29)

где n – число наблюдений; S – сумма разностей между числом последовательностей и числом инверсий по второму признаку.

Расчёт данного коэффициента выполняется в следующей последовательности:

1. Значения Х ранжируются в порядке возрастания (убывания).

2. Значения Y располагаются в порядке, соответствующем значениям Х.

3. Для каждого ранга Y определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа, определяется величина Р, как мера соответствия последовательностей рангов по Х и Y и учитывается со знаком «+».

4. Для каждого ранга Y определяется число следующих за ним значений рангов, меньшим его величины. Суммарная величина обозначается через Q и фиксируется со знаком «-».

5. Определяется сумма баллов по всем членам ряда.

Как правило, коэффициент Кендалла меньше коэффициента Спирмена. При достаточно большом объёме совокупности значения данных коэффициентов имеют следующую зависимость:

 =  _х/у. (8.30)

Связь между признаками признаётся статистически значимой, если значения коэффициентов ранговой корреляции Спирмена и Кендалла больше 0,5.

Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации) W, который вычисляется по формуле

W = , (8.31)

где m – количество факторов, n – число наблюдений,

S – отклонение суммы квадратов рангов от средней квадратов рангов.

Ранговые коэффициенты Спирмена, Кендалла и конкордации имеют то преимущество, что с помощью их можно измерять и оценивать связи как между количественными, так и между атрибутивными признаками, которые поддаются ранжированию.