Сферические зеркала

Сферическое зеркало представляет собой отполированную поверхность шарового сегмента. Прямая проведённая через центр сферы (оптический центр зеркала) и вершину шарового сегмента (полюс зеркала), называется главной оптической осью зеркала. Всякая другая прямая, проходящая через оптический центр, называется побочной оптической осью. Луч параллельный главной оптической оси, после отражения пересекает её в фокусе зеркала, лежащем на расстоянии от зеркала, где R – радиус кривизны зеркала. В случае выпуклого зеркала главную оптическую ось пересекает не сам отражённый луч, а его мнимое продолжение. В этом случае фокус мнимый. Плоскость, проведённая через фокус перпендикулярно главной оптической оси, называется фокальной плоскостью данного зеркала. Лучи параллельные побочной оптической оси после отражения сходятся в точке лежащей на фокальной плоскости зеркала. Расстояние d от предмета до зеркала, расстояние f от зеркала до изображения и фокусное расстояние F связаны формулой.

Знаки перед каждым членом формулы зеркала выбираются по правилу: если предмет (источник) , изображение и фокус являются действительными , то перед соответствующими членами ставится плюс, если мнимыми то минус.

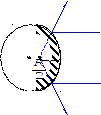
Интерференция света в тонком клине

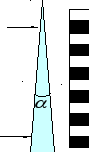
Число полос на единицу длины: , где k – полное число полос, l – суммарная ширина этих полос, - длинна волны, n –показатель преломления материала.

Матричная оптика

Для анализа вопроса распространения световых лучей через сложные оптические системы удобным оказывается аппарат матричной оптики. Будем считать лучи параксиальными, то есть углы их относительно оси столь малыми, что можно считать . Будем рассматривать движение лучей только в осевой плоскости, то есть не будем рассматривать лучей, образующих с осью конфигурацию скрещенных прямых. В таком случае произвольный луч в произвольной точке вдоль резонатора можно характеризовать двумя числами: расстоянием от оси r и углом распространения . Посмотрим, как воздействуют на параметры луча два основных преобразования: 1) прохождение расстояния d и 2) прохождение линзы с фокусным расстоянием f (отражение от сферического зеркала будем заменять линзой с тем же фокусным расстоянием, рассматривая вместо движения отраженного луча как бы движение его отражения в плоском зеркале).

И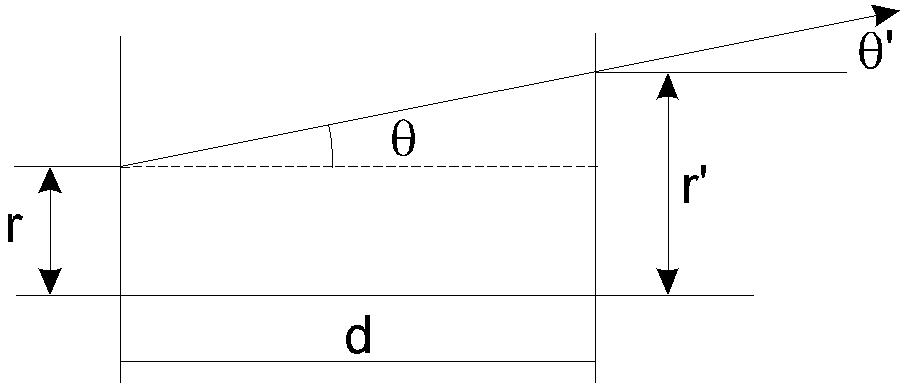 так, если в точке z луч имел характеристики r и , то в точке z + d они примут значения

Рис. Преобразования характеристик луча при прохождении расстояния d.

r₁ = r + d, ₁ = . Если записать характеристики луча в виде столбца , то это преобразование можно представить в матричном виде:

Итак, распространение луча на расстояние d описывается умножением матрицы преобразования

на вектор, описывающий состояние луча.

Рассмотрим теперь прохождение через линзу

Р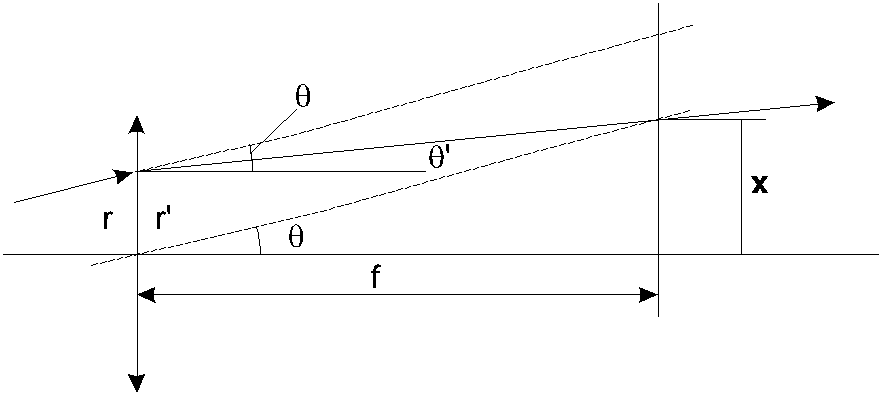 ис. Преобразования характеристик луча при прохождении линзы с фокусным расстоянием f.

Из рисунка видно, что с одной стороны отрезок x равен x = f, а с другой,

x = r + _f. Отсюда . Параметр r при этом остается неизменным, r₁ = r. В матричном виде будем иметь:

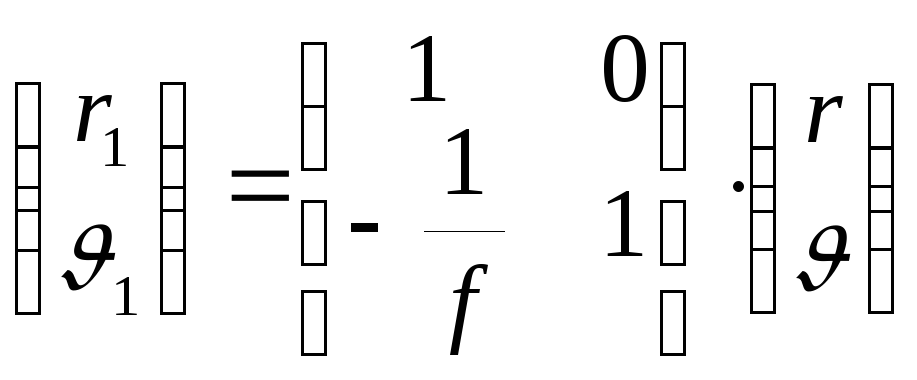
Итак, прохождение линзы с фокусным расстоянием f описывается умножением матрицы преобразования

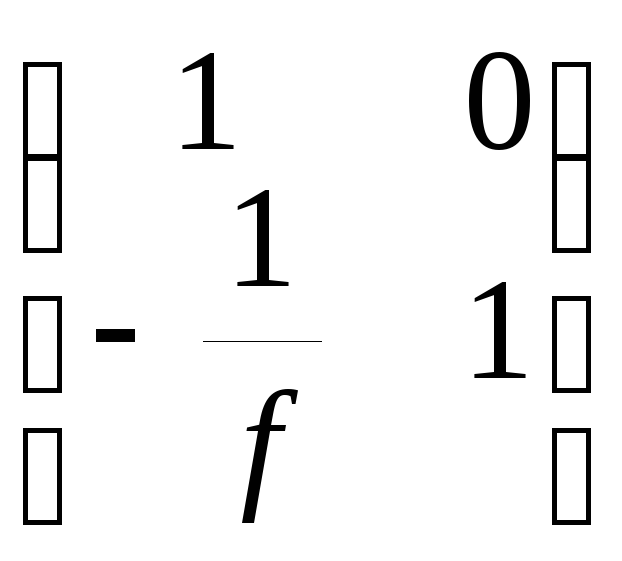
на вектор, описывающий состояние луча. Если линза собирающая (зеркало вогнутое), f считается положительным. В противном случае – отрицательным.

Если луч последовательно проходит линзы и участки свободного распространения, преобразование характеристик луча задается полной матрицей преобразования, которая, как нетрудно видеть, является произведением элементарных матриц преобразования.