
- •Преобразование Лапласа
- •Нахождение изображений
- •Теоремы подобия, смещения, запаздывания
- •Поиск изображения по графику оригинала
- •Отыскание оригинала по изображению
- •Дифференцирование оригиналов и изображений
- •Интегрирование оригиналов и изображений
- •Свертка функций
- •Решение дифференциальных уравнений
- •Решение систем дифференциальных уравнений
- •Решение интегральных уравнений
Поиск изображения по графику оригинала
Пр.9 По данному графику оригинала найти изображение.
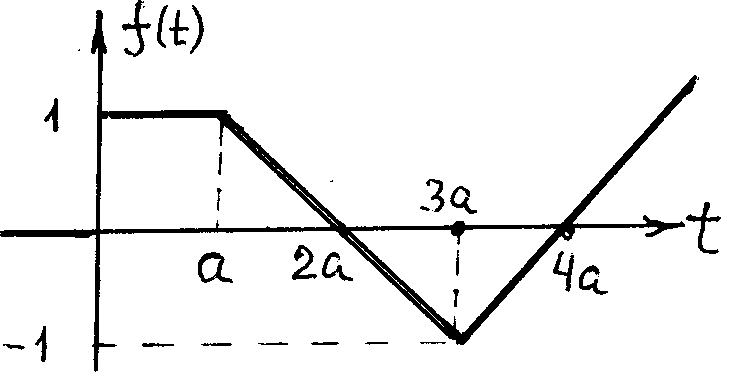
Построим аналитическое выражение для данной функции,
на основе общего уравнения прямой, проходящей через
две
точки (t1,
y1)
, (t2,
y2)
![]() =
=
![]() ( 5 )
( 5 )
и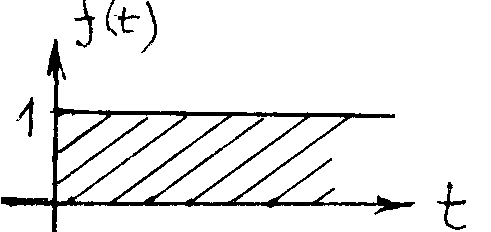
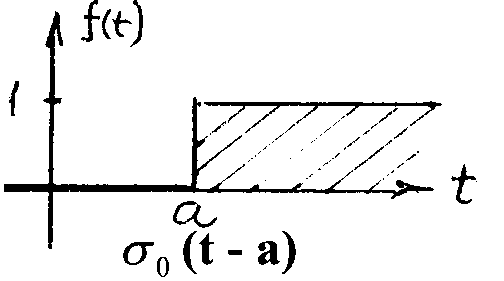
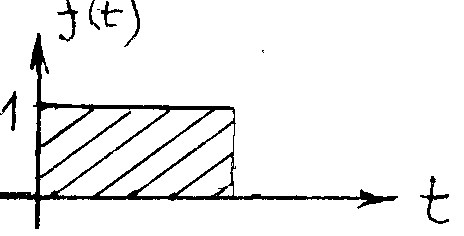 свойств единичной функции
свойств единичной функции
![]() (t
- а) =
(t
- а) =
![]()
![]() (t)
(t)
![]() (t)
-
(t)
-
![]() (t
- а)
(t
- а)
Решение.
Функцию на интервале [0 , a]
описывает разность двух единичных
функций
![]() (t)
-
(t)
-
![]() (t
- а) . Первую наклонную определим из ( 5
) по точкам (2а,
0), (а,
1): y
=-
(t
- а) . Первую наклонную определим из ( 5
) по точкам (2а,
0), (а,
1): y
=-![]() (t
– 2a).
Для перехода от бесконечной прямой к
отрезку на интервале [a,
3a]
умножим уравнение на разность
(t
– 2a).
Для перехода от бесконечной прямой к
отрезку на интервале [a,
3a]
умножим уравнение на разность![]() (t
-а) -
(t
-а) -![]() (t
-3а)
Вторую наклонную определим из ( 5 ) по
точкам (4а,0)
, (3а,-1):
y
=
(t
-3а)
Вторую наклонную определим из ( 5 ) по
точкам (4а,0)
, (3а,-1):
y
=![]() (t
– 4a),
и умножим уравнение на
(t
– 4a),
и умножим уравнение на
![]() (t
- 3а).
Сумма этих трех выражений определит
аналитический вид функции
(t
- 3а).
Сумма этих трех выражений определит
аналитический вид функции
f(t)
=
![]() (t)
-
(t)
-
![]() (t
- а) -
(t
- а) -
![]() (t
– 2a)
[
(t
– 2a)
[![]() (t
- а) -
(t
- а) -
![]() (t
- 3а)]
+
(t
- 3а)]
+
![]() (t
– 4a)
[
(t
– 4a)
[![]() (t
- 3а)]
(t
- 3а)]
Представим
f(t)
в виде суммы слагаемых двух типов
![]() (t
- b)
и (t
– b)
(t
- b)
и (t
– b)![]() (t
- b)
(t
- b)
f(t)
=![]() (t)
-
(t)
-![]() (t
- а) -
(t
- а) -![]() (t
– a)
(t
– a)![]() (t
- а) +
(t
- а) +![]() (t
- а) +
(t
- а) +![]() (t
– 3a)
(t
– 3a)![]() (t
- 3а)
+
(t
- 3а)
+![]() (t
- 3а)+
(t
- 3а)+
+
![]() (t
– 3a)
(t
– 3a)
![]() (t
- 3а)
-
(t
- 3а)
-
![]() (t
- 3а)
=
(t
- 3а)
=
![]() (t)
-
(t)
-
![]() (t
– a)
(t
– a)![]() (t
- а)
+
(t
- а)
+
![]() (t
–
3a)
(t
–
3a)![]() (t
- 3а)
(t
- 3а)
С помощью соотношений Пр.8 совершим переход к искомому изображению
F(t)
=:
![]() -
-
![]()
![]() +
+
![]()
![]() .
.
Таблица изображений
-
№
f(t) при t>0
F(p)
№
f(t) при t>0
F(p)
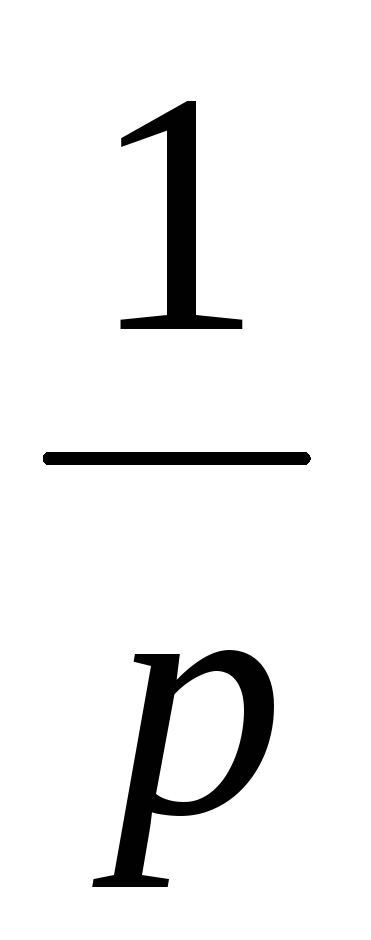
1
1
9
t cos at
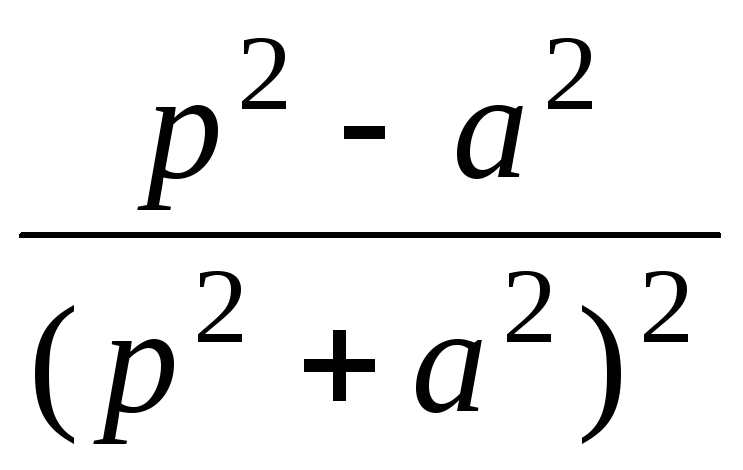
2
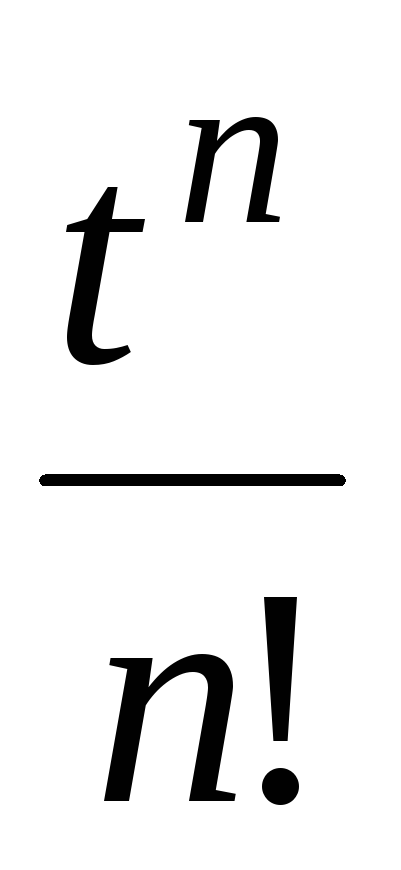
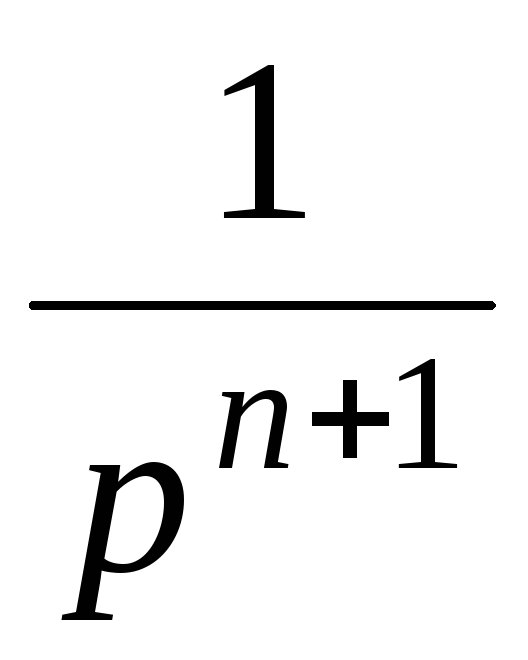
10
t sin at
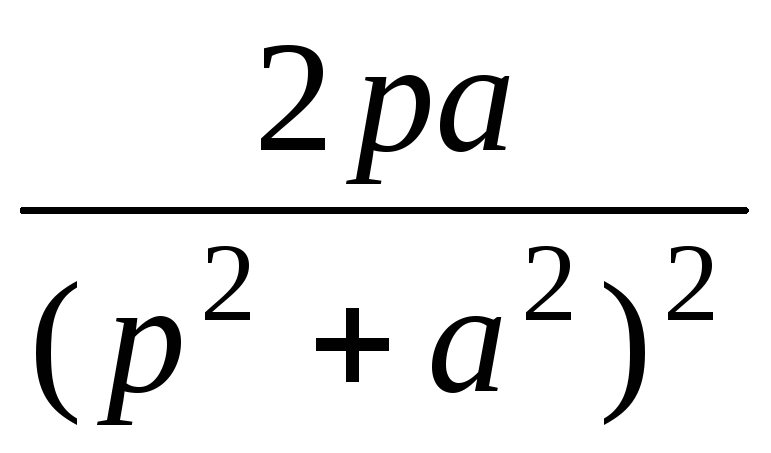
3
eat
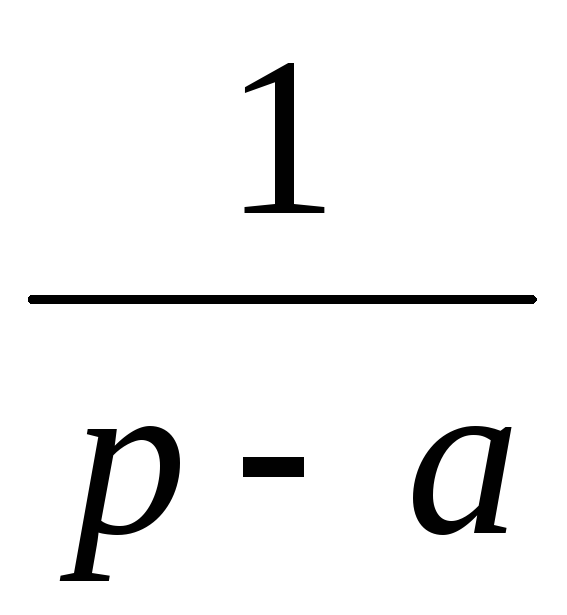
11
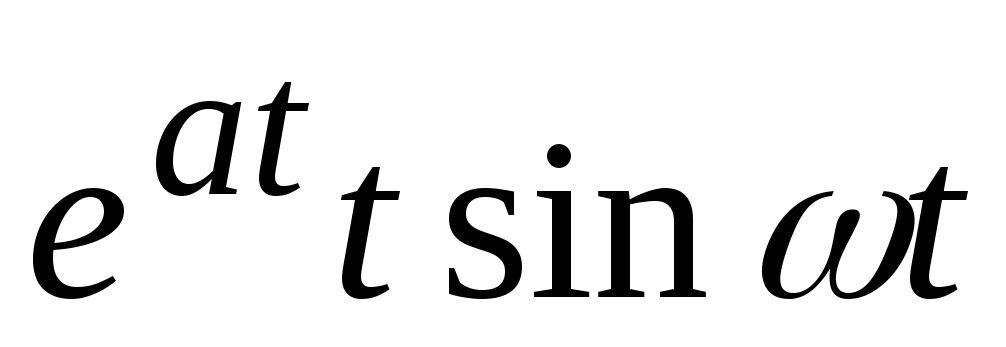
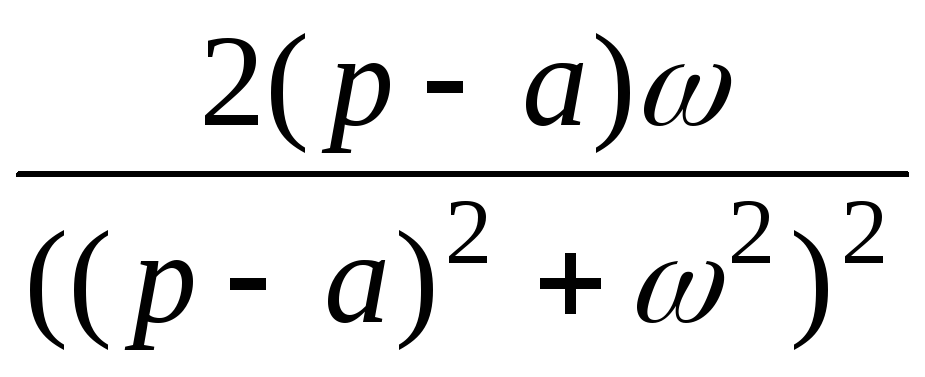
4
cos at
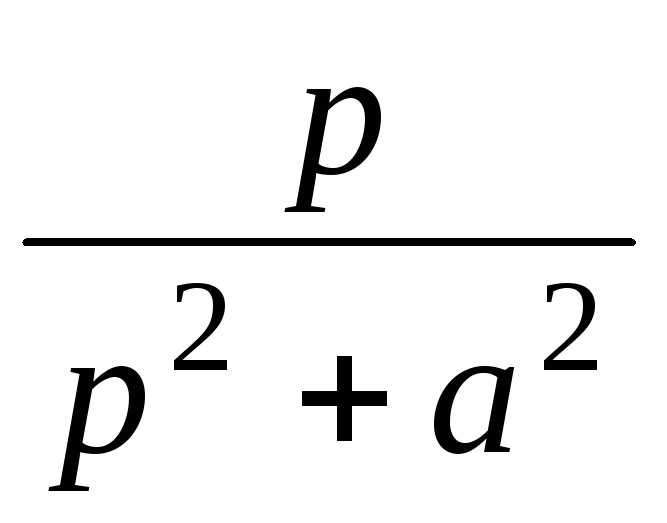
12
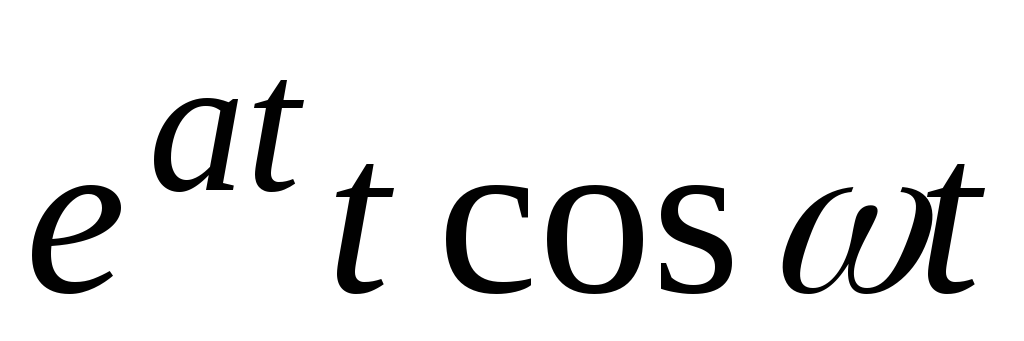
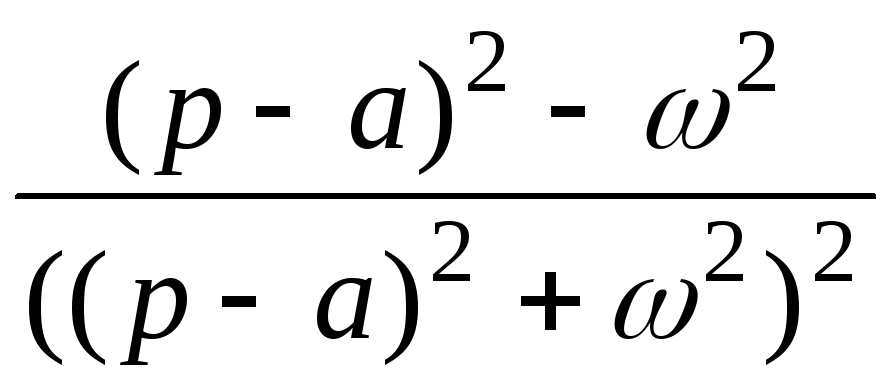
5
sin at
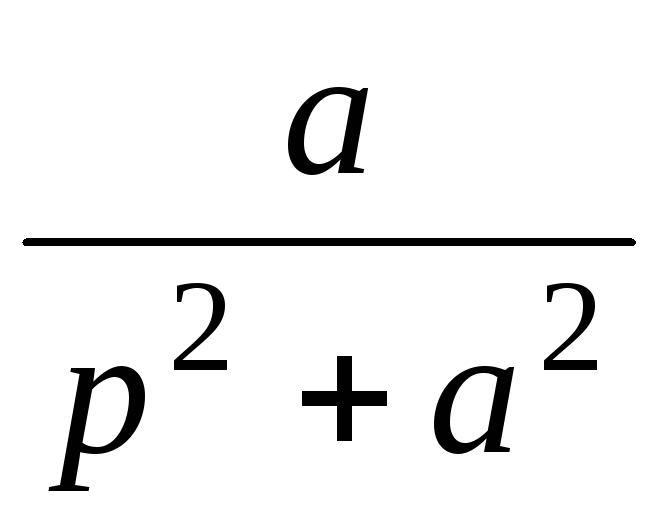
13
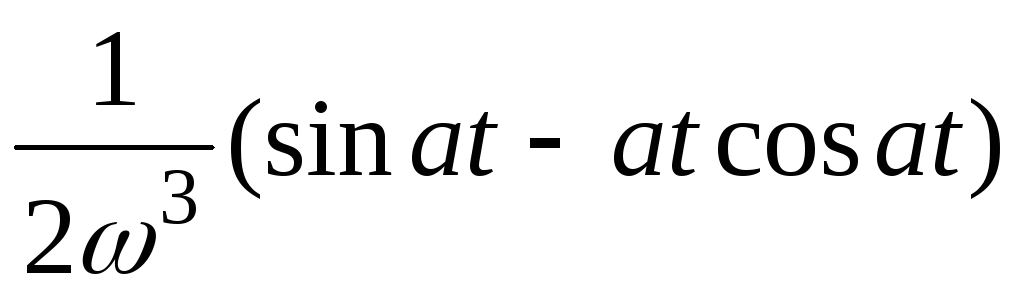
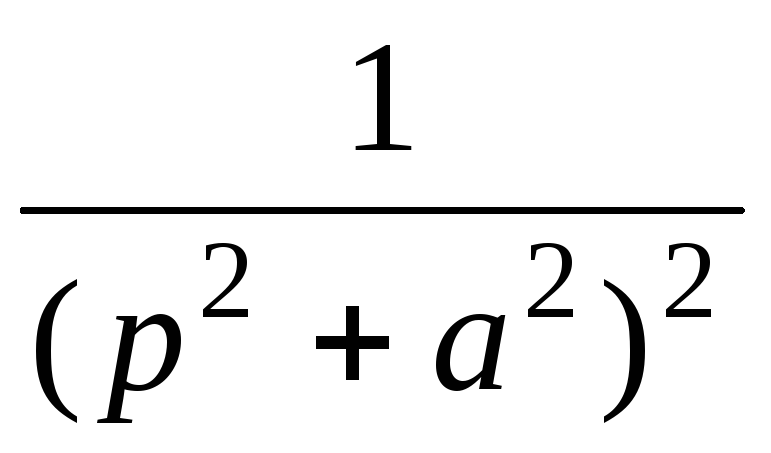
6
ezt cos at
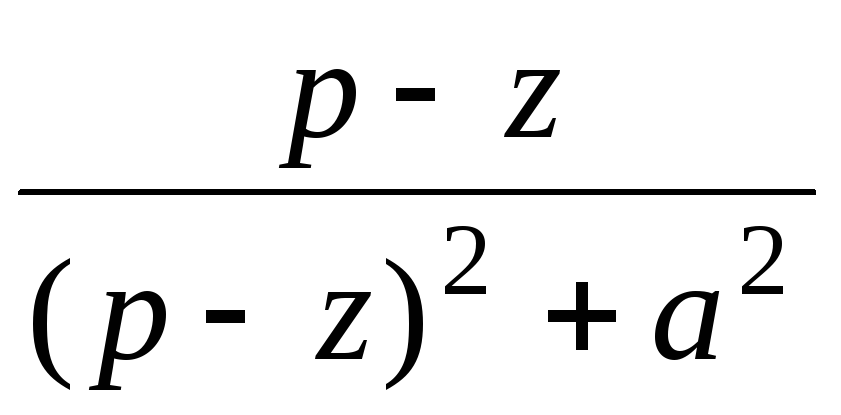
14
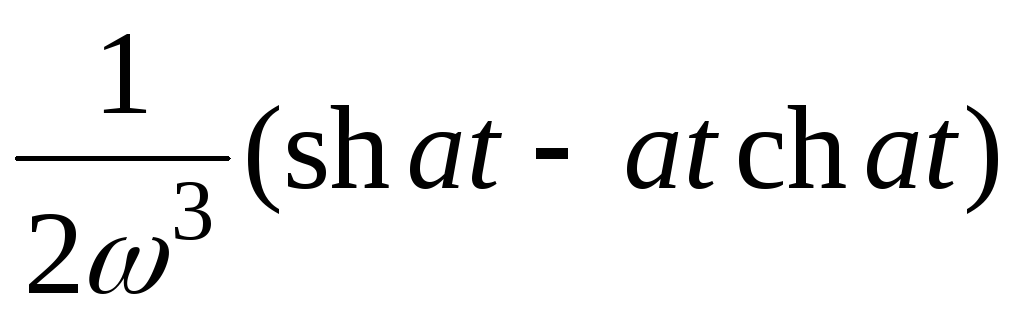
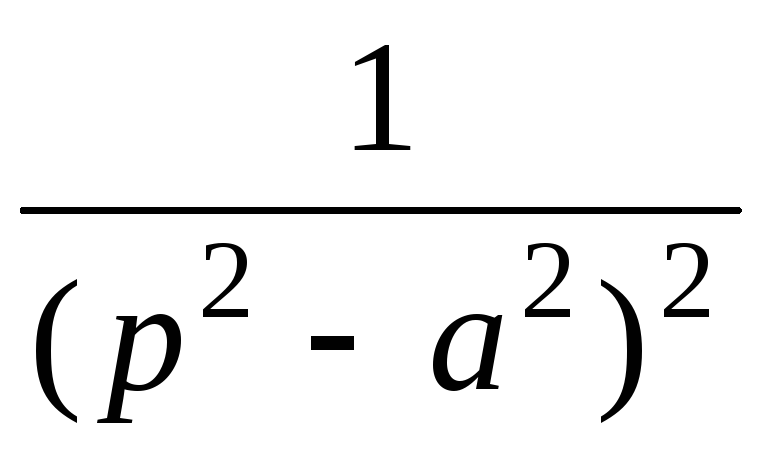
7
ezt sin at
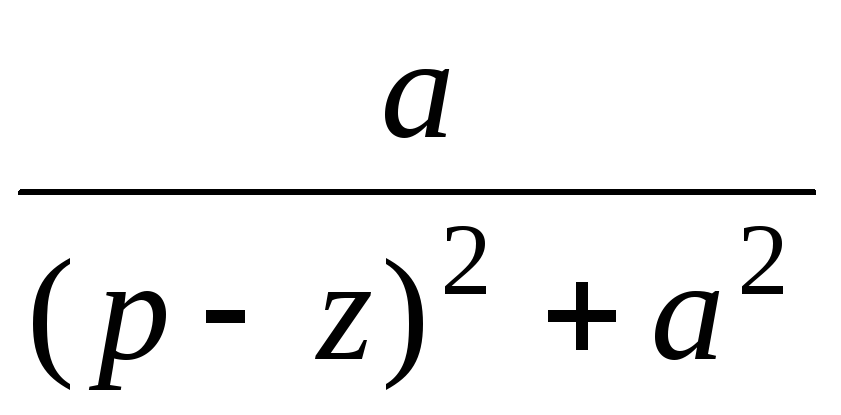
15
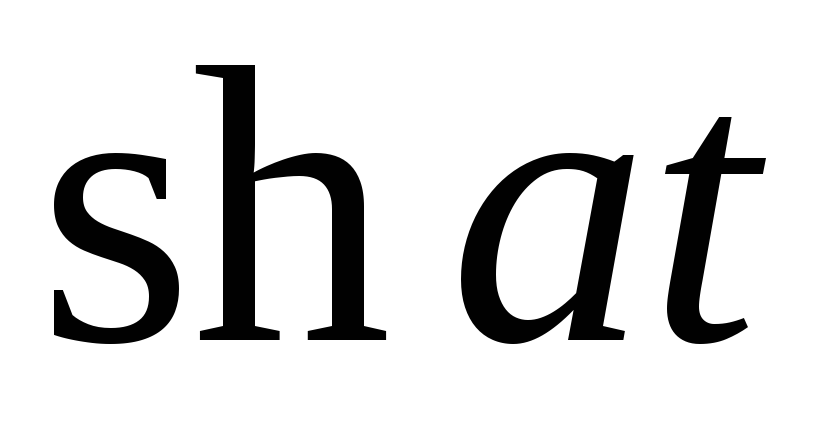
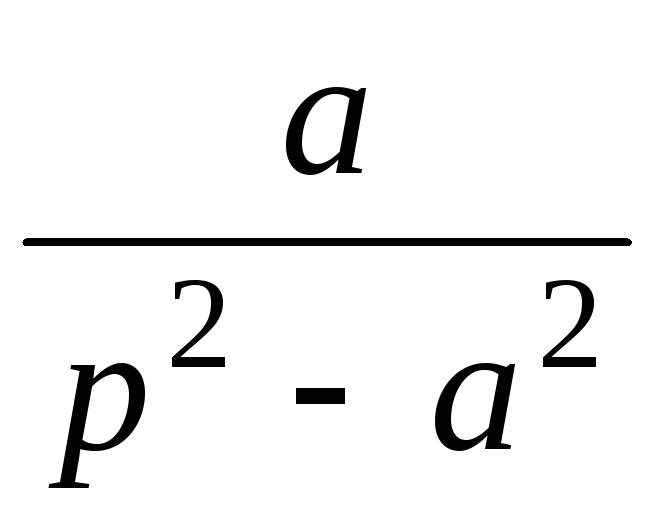
8
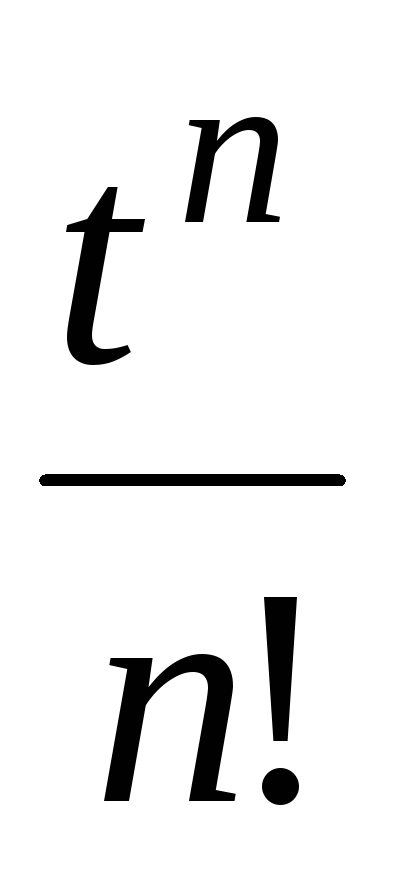 eat
eat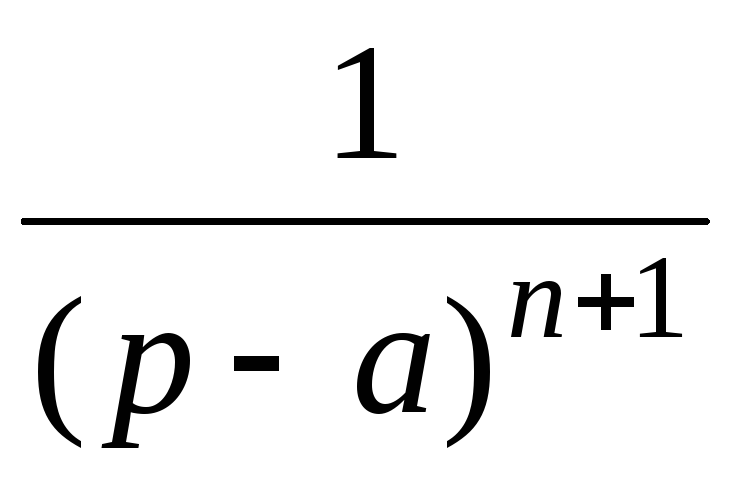
16
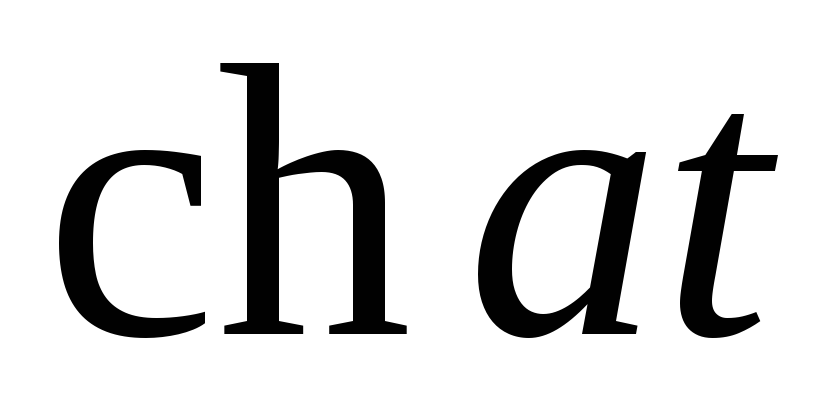
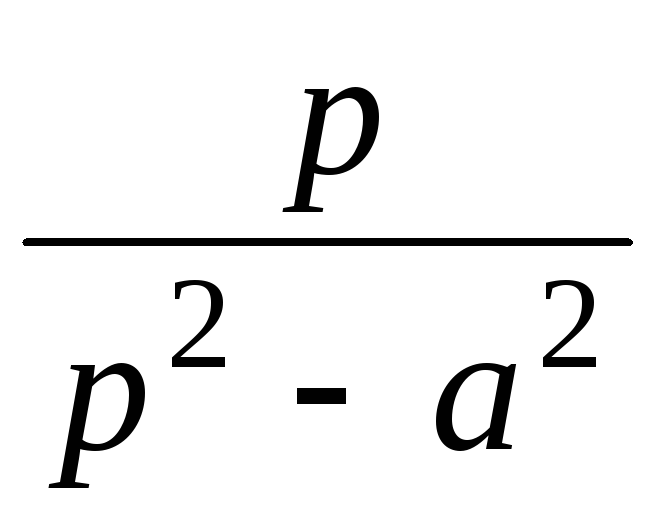
Отыскание оригинала по изображению
Если
изображение является дробно-рациональной
функцией F(p)
=
![]() и m
< n
,
то многочлен
знаменателя представим в виде произ-ведения
линейных множителей
и m
< n
,
то многочлен
знаменателя представим в виде произ-ведения
линейных множителей
![]() =
=
![]() .
Корни
многочлена pi
могут
быть
действительными числами, комплексными
числами и кратными. Комплексные корни
входят сопряженными парами и приводят
к трехчленам типа ( p2
+
.
Корни
многочлена pi
могут
быть
действительными числами, комплексными
числами и кратными. Комплексные корни
входят сопряженными парами и приводят
к трехчленам типа ( p2
+
![]() p
+
p
+
![]() ).
В результате F(p)
представ-ляется в виде суммы
элементарных
дробей типа
).
В результате F(p)
представ-ляется в виде суммы
элементарных
дробей типа
![]() ,
,
![]() (метод неопределенных коэффициентов).
Комбинируя эти дроби, можно пытаться
построить изображения основных
элементарных функций и затем по таблице
восстановить оригинал.
(метод неопределенных коэффициентов).
Комбинируя эти дроби, можно пытаться
построить изображения основных
элементарных функций и затем по таблице
восстановить оригинал.
Пр.
10 Найти оригинал функции F(p)
=
![]() .
.
![]() =
=
![]() =
=
![]() + ½
+ ½![]() =:
etcos
2t
+ ½ etsin
2t
=:
etcos
2t
+ ½ etsin
2t
Пр.
11 Найти оригинал функции F(p)
=
![]() .
.
![]() =
=
![]() =
=
![]() +
+
![]() = =
= =![]()
p2 | A + B = 0
p1
| 2A – 2B + C = 0
![]() A = 1/12 , B = -1/12 , C = - 1/3
A = 1/12 , B = -1/12 , C = - 1/3
p0 | 4A – 2C = 1
![]() =
=
![]()
![]() -
-
![]()
![]() =
=
![]()
![]() -
-
![]()
![]()
Из
формул
№ 3, 6, 7
![]() оригинал
f(t)
=
оригинал
f(t)
=![]() e2t
-
e2t
-
![]() e-t
(cos t
e-t
(cos t![]() +
+![]() sin t
sin t![]() )
.
)
.
Если
в F(p)
только простые нули :
![]() =
=
![]() ,
то разложение
изображения упрощается
,
то разложение
изображения упрощается
F(p)
=
![]() , где
, где
![]() ( 6 )
( 6 )
Пр.12
Найти оригинал функции F(p)
=
![]()
Вычисляем
производную от знаменателя
![]() = [ p(p
– 1)(p
– 2)(p
– 3) ]` =
= [ p(p
– 1)(p
– 2)(p
– 3) ]` =
= (p – 1)(p – 2)(p – 3) + p(p – 2)(p – 3) + p(p – 1)(p – 3) + p(p – 1)(p – 2),
находим её значения в нулевых точках v4`(0) = - 6 , v4`(1) = 2 , v4`(2) = - 2 , v4`(3) = 6 , определяем коэффициенты A0 = - 1/6 , A1 = 1, A2 = - 3/2, A3 = 2/3
и по формуле ( 6 ) расписываем разложение изображения на простые дроби
F(p)
=
![]() =:
=:
![]() +
+
![]() -
-
![]() +
+
![]() .
.
Если F(p) разлагается в сходящийся ряд
F(p)
=
![]() +
+
![]() +
+
![]() + . . . +
+ . . . +
![]() + . . . ,
+ . . . ,
то его оригинал находится по формуле
f(t)
=
![]() +
+
![]() +
+
![]() + . . . +
+ . . . +
![]() + . . .
+ . . .
Этот ряд сходится при всех значениях t .
Пр.13
Найти оригинал функции F(p)
=
![]() .
.
Используем формулу для суммы бесконечной геометрической прогрессии
![]() =
=![]()
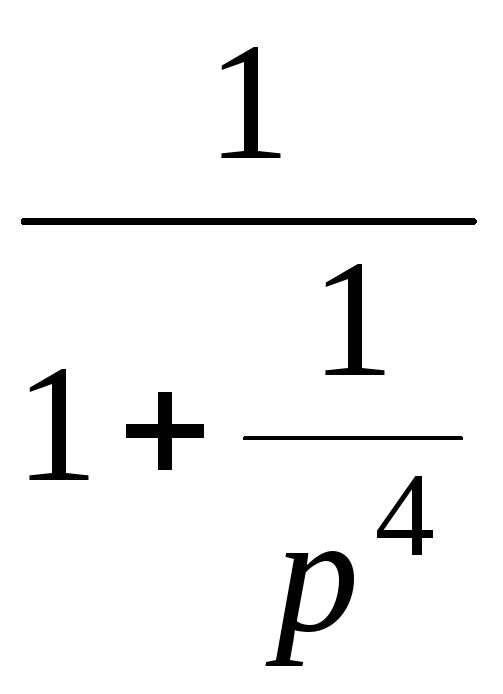 =
=
![]() -
-
![]() +
+
![]() - . . . Этот ряд сходится при |p|
> 1
- . . . Этот ряд сходится при |p|
> 1
По
формуле № 2 получаем оригинал f(t)
=
![]() -
-
![]() +
+
![]() -
-
![]() + . . .
+ . . .
