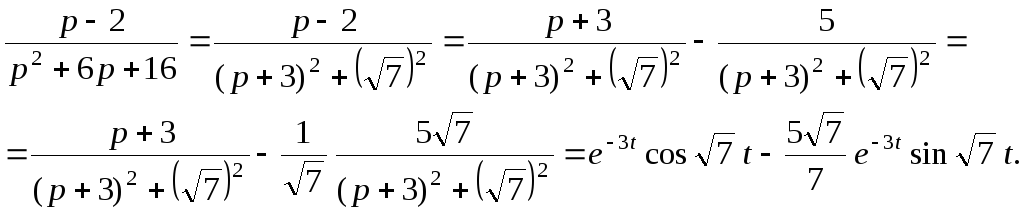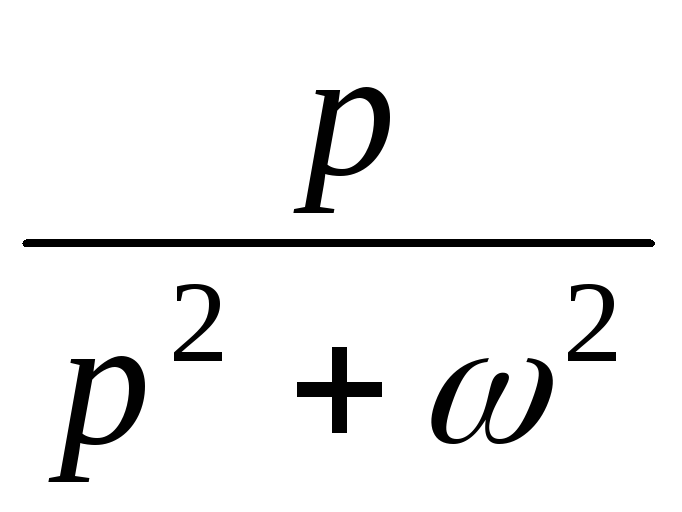Между основными оригиналами и изображениями

Функция – оригинал (f(t)	Изображение F(p)
1
cos t
sin t

Примеры нахождения изображений сложных функций

 1.  .

Так как

 

, то применяя теорему дифференцирования,

найдем

 

Следовательно,

.

 2.

Применять теорему дифференцирования пять раз, конечно, неудобно. Представим в виде

 Так как

, то по теореме смещения изображения

 

 Теперь по теореме линейности находим

 

   3.

Представим в видеДля функции  изображение известно:

 

По теореме дифференцирования изображения - . Следовательно,

 

   4.

 

Так как

то

5.

Так как то

Учитывая, что , по теоремам подобия и линейности получим

 

 Замечания.

1. Грубой ошибкой будет представление изображения заданных функций в виде произведения изображений, соответствующих каждому из сомножителей, так как умножению оригиналов в пространстве оригиналов соответствует другая операция в пространстве изображений [4,5].

2. Решение приведенных задач возможно различными способами. В пособии указан лишь один из возможных способов решения.

3.2. Обратное преобразование Лапласа

При практическом применении преобразования Лапласа всегда приходится решать обратную задачу - построение оригинала по его изображению. Общий метод построения оригинала f(t) по заданному изображению F(p) базируется на теореме обращения  ( формуле Меллина ):

(3.22)

 

где интегрирование проводится по любой бесконечной прямой 7  0Re p =  7g 0, лежащей в полуплоскости абсолютной сходимости интеграла Лапласа [7,8]. Непосредственно формулой (3.22) для нахождения оригинала по известному изображению пользуютя редко. При нахождении оригинала по его изображению обычно применяют таблицы соответствия между оригиналами и их изображениями [5] и свойства преобразования Лапласа.

В самом распространенном случае, когда изображение F(p) является дробно - рациональной функцией вида

 

,

 где A(p) и B(p) - многочлены, причем степень многочлена B(p) больше степени многочлена A(p), оригинал может быть найден разложением дроби A(p) /B(p) на простейшие.

 Пример.  Дано изображение

 

 

Найти оригинал f(t) = F(p).

Разложим заданную дробь на простейшие:

 

 

Приводя к общему знаменателю, получим

.

При p = 0 1 = -8A,

При p = 2  5 = 16B,

следовательно, A = -1/8, B = 5/16.

Приравнивая далее коэффициенты, например, при ив левой и правой частях равенства, получим

Поэтому

 

Применяя теорему линейности, окончательно найдем

 

 Пример. Найти оригинал по его изображению

 

Разложение данной дроби на простейшие имеет вид

 

После приведения к общему знаменателю получим

При p = 0 1 = -3A, откуда A = - 1/3;

при p = 3 1 = 9C, откуда C = 1/9.

Приравнивая далее коэффициенты при в правой и левой частях равенства, получим уравнение 0 = B + C, из которого следует B = - 1/9.

Итак,

 

  Если знаменатель рациональной дроби B(p) имеет простые не-

нулевые корни , то есть если

то оригинал функции F(p) может быть найден по формуле

(3.23)

 

 Пример.  Найти оригинал по его изображению

 

 

Здесь,

Корни знаменателя . Следовательно,

Поэтому

 

 

Если один из простых корней знаменателя B(p) равен нулю, то есть B(p) можно представить в виде , где, то оригинал находится по формуле

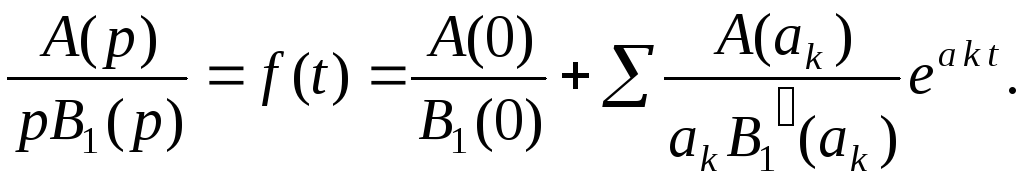(3.24)

 

Здесь суммирование распространяется на все ненулевые корни

многочлена

 Пример.  Найти оригинал по его изображению

 

.

 Здесь

Корни знаменателя . Поэтому

Применяя формулу (3.24), находим

 

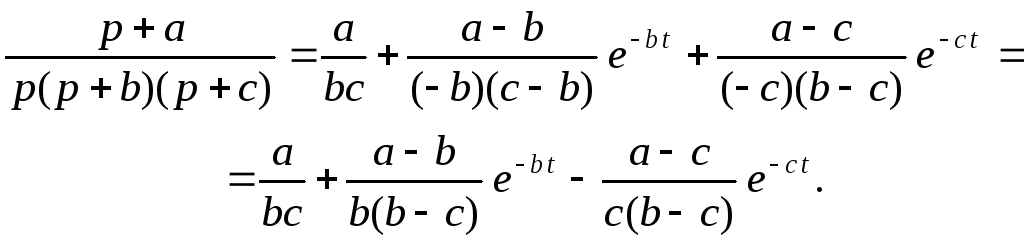
Если знаменатель рациональной дроби представляет собой квадратный трехчлен, корни которого комплексные, удобно представить его в виде суммы квадратов слагаемых и применить теорему смещения изображения.

 Пример.  Найти оригинал по его изображению