49

А.А.Любкин

Введение в математический анализ Краткое содержание лекций по математическому анализу для студентов 1-го курса Экономического факультета мгу (теория).

Введение

Это, за указанными в тексте исключениями(их всего одно или два), – реально прочитанная теория.

Автор всю жизнь придерживался убеждения, что если читать курс математической дисциплины даже не на естественном факультете, он всё равно должен быть построен так, чтобы те студенты, которые хотят понять, откуда берутся те или другие утверждения, смогли бы это понять. Все утверждения , касающиеся последовательностей, доказываются. В дальнейшем доказываются только те утверждения, которые нельзя получить с помощью эквивалентности Гейне-Коши, и все принципиальные теоремы. Необходимые примеры приводятся в минимальных размерах. На лекциях их приводилось гораздо больше, равно как и доказательства сопровождались рисунками и прочими способствующими пониманию подробностями. Предлагаемый текст предназначен только для того, чтобы вся теория была под рукой в сжатом изложении.

Это – не учебник матанализа для среднего студента. Это – справочный материал. При написании автор пользовался(как и при чтении лекций) различными стандартными учебниками ,в основном – «Курсом дифференциального и интегрального исчислений» Г.М.Фихтенгольца,тт.1-3.

.

Первый семестр

Предполагается, что читающий знаком с курсом арифметики, алгебры, тригонометрии и началами геометрии в объёме средней школы. Желательно, но не обязательно, чтобы он знал что-нибудь о понятии производной.

В частности, предполагается, что читатель знает, как выглядят графики функций y=ax+b, y=ax²+bx+c, y=x, y=a^x, y=log_ax, y=sin(x), y=cos(x), y=tg(x), y=ctg(x), y=arcsin(x), y=arccos(x), y=arctg(x), y=arcctg(x).

Для дальнейшего будут существенны следующие свойства функции y = |x|:

|xy|=|x||y|;|x+y| |x|+|y|;|x-y| ||x|-|y||.

Предполагается также, что известны словосочетания: числовая прямая, вещественное число, числовая ось, действительное число, целое число, рациональное число.

Множество натуральных чисел N есть множество {1,2,3…..}.Множество целых чисел Z есть множество {0,-1,+1,-2,+2,….}.Множество рациональных чисел Q есть множество {p/q | p. Множество действительных (или вещественных) чисел будет обозначаться R.

Для стандартных подмножеств множества R будут употребляться обозначения:

[a,b] = }(отрезок); (} (левый полуинтервал); (a,b) = a<x<b} (интервал); [a,b) = {x| a<b}(правый полуинтервал).

Множество типа {x| a} называется замкнутым лучом, равно как и множество вида {x| -< xa}; если убрать знаки равенства, получится открытый луч.

Множество точек числовой оси называется ограниченным, если найдётся отрезок, на котором всё оно расположено.

Пусть >0.

точки называется интервал (a - ,a+). точки a называется проколотой, если рассматриваются все её точки, кроме a. Проколотая окрестность точки a,таким образом, это объединение интервалов (a - ,a )(a , a +).

окрестностью «точки» называется множество точек x числовой оси, для которых >.

1.Кое-что о множествах.

Вопрос о том, что такое множество, здесь обсуждаться не будет. Обычно, когда говорят о множествах, говорящие имеют в виду некое собрание известных им элементов.

Пусть A и B - множества. Их пересечением называется множество C=AB,каждая точка которого принадлежит и A и B.

Объединением множеств A и B называется множество AB ,состоящее из тех, и только тех точек, которые принадлежат либо A,либо B.

Разностью множеств называется множество, состоящее из тех элементов , которые не принадлежат

Симметрической разностью называется множество

1.1.Легко понять, что пересечение двух окрестностей одной точки будет окрестностью этой точки(меньшей по размеру), и объединение двух окрестностей одной точки тоже будет окрестностью этой точки –(большей).Аналогичные утверждения верны для любого конечного числа окрестностей одной и той же точки.

1.2.Множество А точек числовой оси называется ограниченным сверху, если найдётся число М, такое, что для всех xA выполняется неравенство xМ. Число М называется в этом случае верхней гранью множества А. Число М называется точной верхней гранью множества А, если (1) оно является верхней гранью множества А, и (2) если никакое число N <M верхней гранью множества А не является (иными словами, всё множество А лежит на луче(-,М], и в любом полуинтервале (M - ,M] есть хотя бы одна точка xA.Точная верхняя грань множества А обозначается обычно, supA. Точная верхняя грань множества {-x,xA}=-A , взятая с минусом, называется точной нижней гранью множества A и обозначается обычно infA. Множество А называется неограниченным сверху, если у него нет точной верхней грани, и неограниченным снизу, если у него нет точной нижней грани. Мы будем считать, что для числовых множеств выполнена следующая аксиома.

Аксиома. Всякое ограниченное сверху множество А имеет точную верхнюю грань.

У этой аксиомы есть много эквивалентных ей утверждений. Они будут в дальнейшем отмечаться по мере появления. Фактически она означает непрерывность числовой прямой.

2.Теория последовательностей

Определение 2.1. Последовательностью называется бесконечное множество вещественных чисел, занумерованных натуральным рядом, то есть последовательность - это множество{a(n)},каждому элементу которого присвоен некоторый номер; а(n) – это элемент с номером n.

Определение 2.2.Последовательность b(m) называется подпоследовательностью последовательности a(n),если любой её элемент является элементом последовательности a(n),b(m) = a(n) для некоторого n, и для любых m< mвыполняется неравенство n<n, то есть в подпоследовательности элементы идут в том же порядке, что и в последовательности. Иными словами, подпоследовательность получается из последовательности вычёркиванием некоторого, может быть бесконечного, числа элементов, но так, что при этом остаётся бесконечное число элементов, и порядок оставшихся элементов не меняется.

Последовательности можно складывать, вычитать, перемножать , делить, если последовательность в знаменателе не имеет нулевых элементов, и брать от них разнообразные функции( по формуле f{a(n)} = {f(a(n))}).По определению, если {a(n)}и {b(n)} – две последовательности, то (a+b)(n) = a(n) + b(n);(a – b)(n)=a(n) – b(n); (ab)(n) = a(n)b(n); (a /b)(n) = a(n)/b(n);(n) = .Иными словами, все операции над последовательностями, определённые выше, выполняются поэлементно.

2.1.Последовательности ,имеющие предел(сходящиеся последовательности).

Определение 2.3.Говорят, что последовательность a(n) имеет предел l,если для всякого >0 найдётся такой номер n(), что для всякого номера mn() ,будет выполняться неравенство <.Говорят, что последовательность a(n) сходится к l.Иначе можно сказать, последовательность а(n) сходится к l,если для любого > 0 найдётся такая окрестность точки +(а именно, [n(),+) = U(+)), что для всех mn( ) элементы a(m) попадают в -окрестность точки l(которую можно обозначить U(l)). Пишут: .

Примечание. Эта «окрестностная» точка зрения очень важна. Практически все утверждения, которые можно получить с её помощью, сохраняются в том случае, если при определении понятия окрестности оказывается, что две непустых окрестности одной точки пересекаются по непустой окрестности той же точки, и если для некоторой операции ,определяемой для любой пары элементов рассматриваемого множества как ,сохраняются те же свойства, что для обычной абсолютной величины. Более того, доказательства утверждений, приводимые в дальнейшем, достаточно часто выглядят следующим образом: строится несколько окрестностей точки, в каждой из которых выполняется некоторое утверждение; тогда в пересечении этих окрестностей выполняются все утверждения одновременно; обычно выполнение всех этих утверждений обеспечивает доказательство исходного утверждения.

Лемма 2.1.1(об устойчивости знака).Если lim a(n) = l 0, то найдётся окрестность точки +, в которой a(n) имеет тот же знак, что и l.Иными словами, найдётся такой номер т, что для всех тm a(m) будет иметь тот же знак, что и l.

Доказательство. Мы докажем больше, а именно, что если l0, то найдётся номер m, начиная с которого для всех m будет l/2. Действительно, поскольку lim a(m) = l, для всякого >0 найдётся такой номер m, начиная с которого будет <, или, по определению модуля, -<a(m) – l <, или, что то же самое, l - <a(m)< l + . Выбирая теперь = l/2, получим l- < a(m) <l + . Очевидно, левая и правая части этого двойного неравенства имеют один знак. Лемма доказана.

Примечание. Вместо l/2 можно взять l, где [0,1).

Лемма 2.1.2.Последовательность, имеющая предел, ограничена.

Доказательство. Пусть lim a(n) = l. Это означает, что для >0 найдётся номер т,такой, что для всех mmбудет выполняться неравенство l - <a(m)<l + .То есть все элементы последовательности будут лежать на интервале (l - l + ), кроме конечного числа m- 1 ,которые там , может быть , не лежат. Расширив полученный интервал до отрезка, включающего все эти элементы, получим, что лемма доказана.

Определение 2.4. Если lim a(n) = 0, говорят, что последовательность a(n) бесконечномалая.

Лемма 2.1.3.Произведение ограниченной последовательности на бесконечномалую является бесконечномалой последовательностью. Сумма бесконечномалых последовательностей в конечном числе является бесконечномалой последовательностью.Модуль бесконечномалой последовательности – бесконечномалая.

Доказательство.(a).Пусть a(n) – бесконечномалая, а b(n) – ограниченная.Тогда существует такой номер n,что для всех nбудет выполняться неравенство M для некоторого M(ограниченность), и для произвольного при = найдётся такой номер n,что для всех nбудет выполняться неравенство .Тогда для n имеем < . Значит,a(n)b(n) – бесконечномалая.

(б).Пусть a(n),b(n) –бесконечномалые. Пусть - произвольно. Для произвольных ,в частности, для найдутся такие номера n,n,соответственно, что будут иметь место неравенства при n,n,соответственно. Значит, при n, и a(n) + b(n) – бесконечномалая.

Для модуля доказательство очевидно из определения бесконечномалой.Лемма доказана.

Замечание. Вместо двух бесконечномалых можно было взять их любое конечное количество. Доказательство очевидно.

Лемма 2.1.4.Если lima(n) = l, то - бесконечномалая, и наоборот,если - бесконечномалая, то lima(n) = l.

Доказательство очевидно.

Лемма 2.1.5. Пусть lim a(n) = l,lim b(m) = l.Тогда

lim(a(n) + b(n)) = l+l; lim(a(n) – b(n)) = l - l; lim(a(n)b(n)) = ll;lim = и lim = , если b(n) не обращается в 0 и

Доказательство. Во всех случаях достаточно доказать, что разность между правой и левой частями есть бесконечномалая. Имеем:

- по Лемме 2.1.2,сумма бесконечномалых есть

бесконечномалая. Для разности доказательство аналогичное.

- значит, предел модуля равен модулю предела.

Первое слагаемое справа – это произведение ограниченной на бесконечномалую, второе - то же. Значит, предел произведения равен произведению пределов

.

Согласно Лемме 2.1.1.,найдётся n,начиная с которого (то есть, для n ) ,будет , то есть, выражение перед круглой скобкой будет ограничено. Оба выражения в круглых скобках будут бесконечномалыми. Значит, всё выражение будет бесконечномалым, и, значит, предел частного будет равен частному пределов.

Лемма доказана

Лемма 2.1.6.Пусть Тогда, если начиная с некоторого , то .

Доказательство. Предположим, что . Тогда Согласно лемме об устойчивости знака, начиная с некоторого будет выполняться неравенство что противоречит условию.

Лемма доказана.

Замечание. Нельзя утверждать, что Пусть, например, .Очевидно, начиная с ,, но .

Лемма 2.1.7(о двух милиционерах). Пусть , начиная с некоторого Тогда, если то существует и

Доказательство. Пусть взято произвольно. Согласно условию, начиная с некоторого , будет , а начиная с некоторого будет .Тогда при имеем: ,или

Лемма доказана.

Лемма 2.1.8. Возрастающая ограниченная сверху последовательность имеет предел.

Доказательство. Поскольку последовательность ограничена, у неё есть точная верхняя грань (согласно аксиоме!) . Пусть взято произвольно. Рассмотрим полуинтервал (. Найдётся элемент последовательности , принадлежащий этому полуинтервалу (в противном случае не есть точная верхняя грань ). Поскольку последовательность - возрастающая, для всех будет принадлежать тому же полуинтервалу, то есть будет выполняться неравенство (Знакв этих условиях невозможен. Почему? ). Согласно определению предела последовательности,

Лемма доказана.

Следствие. Всякая неубывающая последовательность, ограниченная сверху, имеет предел. Всякая невозрастающая последовательность, ограниченная снизу, имеет предел.

Лемма 2.1.9(о стягивающихся отрезках).Пусть дана последовательность отрезков , удовлетворяющая следующим трём условиям:(1) для всякого , (2) для всякого одновременно выполняются неравенства и (3)Тогда существует ровно одна точка, принадлежащая всем этим отрезкам.

Доказательство. Рассмотрим две последовательности: последовательность левых концов,, и последовательность правых концов,.Первая из них неубывающая и ограниченная сверху, вторая – невозрастающая и ограниченная снизу. По предыдущему следствию, обе они имеют пределы и , соответственно. Поскольку для любого и для любого всегда будет , то будут выполняться и неравенства и.Следовательно, .В частности, при получим , откуда .Предел выражения справа равен 0 по условию. Значит, . Лемма доказана.

Примечание 1. Леммы 2.1.7 и 2.1.8 эквивалентны основной Аксиоме.

Примечание 2. Если в условии Леммы заменить отрезки на интервалы или полуинтервалы, её утверждение, вообще говоря, не будет иметь места. Если же отказаться от условия (3), то общих точек будет много, целый отрезок

2.2.Последовательности, не имеющие предела.

Определение 2.5.Точка называется предельной точкой последовательности (множества ), если в любой проколотой окрестности этой точки есть хотя бы один элемент последовательности (множества ).

Определение 2.6. Точка называется изолированной точкой множества , если она принадлежит множеству и если существует окрестность точки , в которой нет других точек множества .

Примеры: (1) У последовательности все точки – изолированные.

(2) У последовательности 1;1;2;1:3;1;4;…… точка 1 является предельной.

Лемма 2.2.1. Всякая ограниченная последовательность имеет хотя бы одну предельную точку, и существует подпоследовательность, сходящаяся к этой точке.

Доказательство. Оба утверждения будут доказываться вместе. Пусть - рассматриваемая последовательность. Она по условию ограничена, значит у неё существуют конечные точные грани, нижняя - , и верхняя - . Все элементы лежат на отрезке поделим его пополам. Хотя бы на одной из половин будет лежать бесконечное число элементов последовательности (в противном случае их число было бы конечным на всём ). Из элементов, лежащих на этой половине, произвольно выберем какой-нибудь, например, . Концы этой половины обозначим (слева направо!) .Поделим выбранную половину отрезка опять пополам. На одной из двух образовавшихся половин (четвертинок первоначального ) опять окажется бесконечное число элементов . Выберем среди них элемент так чтобы было , обозначим концы выбранной половинки и продолжим деление пополам. Те половинки, которые мы выбираем, образуют систему стягивающихся отрезков , по длине стремящихся к 0. У них, по Лемме о стягивающихся отрезках, есть общая точка . Элементы , которые мы выбирали, образуют подпоследовательность последовательности ,так как номера возрастают. Покажем, что - предел этой подпоследовательности. Если выбрано произвольно, мы всегда можем указать номер , для которого длина очередной половинки будет меньше, чем .Так как илежат на этой половинке, и все последующие для будут лежать там же, то неравенство будет выполняться для всех Значит, . В любой проколотой окрестности точки будет содержаться хотя бы одна точка последовательности (в силу правила выбора половинок отрезков). Значит, будет предельной точкой последовательности

Лемма доказана.

Если последовательность не ограничена, она может не иметь предельных точек:

(1) , или (2) иметь: . В случае (2) предельных точек может быть сколько угодно (например, вся числовая прямая, то есть все действительные числа могут быть предельными точками одной последовательности). Для ограниченных последовательностей предельные точки могут иметься в любом конечном количестве, или их число может быть бесконечным, в частности, они могут заполнять отрезок, полуинтервал или интервал.

Определение 2.7.Точная нижняя грань множества предельных точек последовательности (конечная или бесконечная) называется нижним пределом последовательности и обозначается ; точная верхняя грань множества предельных точек последовательности (конечная или бесконечная) называется верхним пределом последовательности и обозначается .

Примеры:1.У последовательности ;2.У последовательности ;3.У последовательности .

Лемма 2.2.2.(Критерий Коши). Для того чтобы последовательность сходилась, необходимо и достаточно, чтобы для неё выполнялось следующее условие(условие Коши): для всякого существует , такое, что для любых имеет место неравенство.

Доказательство.(1) Необходимость: если последовательность сходится, условие выполняется. Если , то по найдётся такой номер , что для всех будет выполняться неравенство .Для любых будем иметь

Условие выполнено.

(2) Достаточность. Если условие выполнено, последовательность сходится. Пусть условие выполнено. Возьмём какое-нибудь , найдём по нему .Тогда для всех будет выполняться неравенство или . Отсюда следует, что ограничена (так как вне интервала находится конечное число членов последовательности). Поскольку ограничена, у неё есть предельные точки. Если предельная точка всего одна, то это и есть .(Почему?) Предположим, что есть две разных предельных точки, . Возьмём . Существуют подпоследовательности последовательности сходящиеся к этим предельным точкам. Пусть подпоследовательность сходится к , а подпоследовательность - к .По выбранному , из условия Коши найдём , такое что для всех ; найдутся также и , такие что для и будут выполняться неравенства и , соответственно. Имеем

если и будут не меньше . Полученное противоречие показывает, что предельная точка у нашей последовательности всего одна. Лемма доказана.

Примечание. Критерий Коши эквивалентен основной Аксиоме.

3.Предел функции

Пусть имеется функция f(x), определённая в проколотой окрестности U(x) (или в одной из полуокрестностей).

Определение 3.1.Пределом функции f(x) в точке x называется число A,если для всякого >0 найдётся >0,такое, что для всех x из U(x),xx,.

Это определение называется определением предела функции по Коши.

Другие формулировки.1.Обозначение .2.Говорят, что предел функции равен A при стремлении точки x к точке , если при стремлении к нулю

разности x-x стремится к нулю разность f(x) – A.3.A = limf(x), если для всякого найдётся такое , что для всех xx,для которых выполняются неравенства ,будут выполняться неравенства.

4..

5.().Символом Uобозначается проколотая окрестность.

Определение 3.2.Число A называется пределом функции ,определённой в некоторой проколотой окрестности точки ,если для любой последовательности точек ,принадлежащей указанной окрестности и сходящейся к , последовательность значений функции сходится к A.

Это определение предела называется определением предела функции по Гейне.

Теорема 3.1.Определения предела функции по Коши и по Гейне эквивалентны.

Доказательство.1.Пусть по Коши. Тогда для любого найдётся , такое, что для всех Пусть теперь - произвольная последовательность, сходящаяся к точке Согласно определению предела последовательности, найдётся такое что при всегда будет Поэтому, начиная с ,будет выполняться неравенство , и мы получили: Значит - предел по Гейне.

2.Пусть теперь по Гейне. Предположим, что по Коши. Тогда найдётся, такое, что для любого 1> найдётся такой , что с одной стороны, а с другой стороны,Множество точек является ограниченным: оно всё принадлежит окрестности Пусть .Тогда но и, значит,Мы нашли последовательность, сходящуюся к и такую, что соответствующая последовательность значений функции не сходится к Это противоречит предположению, что - предел по Гейне.

Теорема доказана.

Следствие 3.1. Леммы 2.1.1 – 2.1.8 справедливы для функций, имеющих предел в точке, при соответствующей переформулировке. А именно

3.1.1.Еслито найдётся окрестность точки в которой значение отличается от менее, чем на ; в частности, знак для всех из этой окрестности будет совпадать со знаком

3.1.2.Если то ,в которой ограничена.

3.1.3.Пусть в некоторой окрестности функция - бесконечномалая при,- ограниченная. Тогда - бесконечномалая. Сумма конечного числа бесконечномалых есть функция бесконечномалая. Модуль бесконечномалой функции – бесконечномалая.

3.1.4.Если то - бесконечномалая функция при и обратно.

3.1.5.Пусть . Тогда ;если то

3.1.6.Если в некоторой окрестности и то

3.1.7.Если в некоторой окрестности и , то

3.1.8.Пусть при монотонно возрастает и ограничена. Тогда

3.2.Критерий Коши для функций. Пусть определена в некоторой .Для того, чтобы существовал , необходимо и достаточно, чтобы для любого нашлось такое, что для любых из ,для которых , выполнялось неравенство

Все эти утверждения доказываются либо непосредственно из определения предела функции, либо ссылкой на то, что аналогичные утверждения верны для последовательностей и Теорему 3.1.

Докажем, например,3.1.8.Пусть выполнены условия 3.1.8,и пусть монотонно возрастая. Тогда монотонно возрастает и ограничена сверху, и, значит, имеет предел А. Пусть , для всех ,тоже монотонно возрастая. Тогда последовательность тоже будет монотонно возрастающей и ограниченной и, значит, будет иметь предел В. Но такое, что,и ,значит,,откуда .По аналогичной причине, .Следовательно, , и всё доказано.(Почему? Что будет, если , не монотонно?)

3.3. Нечто об эквивалентности и - малых.

Пусть при (где может быть и бесконечностью,) или оба этих предела равны .

Определение 3.3.Пишут , если ,( и говорят, что (при ) убывает быстрее, чем , или что (при ) растёт медленнее, чем ).

Это определение можно использовать и при условии, что .В этом случае равенство означает, что - б.м. при .(Почему?).Тот же факт можно записать как .Вообще, выражение может (при нашем определении символа ) означать только б.м.

Лемма 3.3.1.

Доказательство. Оба равенства означают, .

Лемма 3.3.2. (1)(2) ;(3) при имеет место включение ; при включение обратное.

Определение 3.4.При пишут, что ,если и только если .Говорят, что в этом случае и эквивалентны.

Лемма 3.3.3..

Проверяется по определению.

Лемма 3.3.4. При вычислении пределов произведений и частных функции можно заменять на эквивалентные.

Доказательство. Пусть,исуществует. Тогда (по 3.1.1);для произведения – аналогично

4.Непрерывность.

Определение 4.1.Функция называется непрерывной в точке ,если она определена в некоторой окрестности этой точки и . 1.Определение непрерывности по :функция называется непрерывной в точке ,если она определена в некоторой окрестности точки и для точек из этой окрестности . 2.Определение непрерывности с помощью окрестностей: называется непрерывной в точке ,если для всякой .

Понятно, что все эти определения эквивалентны. Они означают, что по любой окрестности точки можно найти окрестность точки ,которая при отображении с помощью функции целиком попадает в выбранную заранее окрестность точки .Иными словами, при малом изменении мало меняется

Свойства 3.1.5 – 3.1.7 имеют место для непрерывных функций при естественных переформулировках. Один факт отметим специально.

Теорема 4.1. Если функции и определены в некоторой окрестности точки и непрерывны в точке , то в этой точке будут непрерывны и функции (последняя – при естественном ограничении ).

Определение 4.2.Пусть функция определена в некоторой окрестности точки , а функция - в некоторой окрестности точки , и пусть Функция , определённая в окрестности , называется сложной функцией от

Теорема 4.2.Если непрерывна в точке , а - в точке , то непрерывна в точке .

Доказательство. Нам нужно вычислить .При (по непрерывности ). Для функции это значит(по непрерывности , что она стремится к Теорема доказана.

Примечание. (Точки разрыва).Если не является непрерывной в точке ,хотя и определена в некоторой окрестности этой точки(включая саму эту точку или нет), говорят, что функция разрывна в точке .Если при этом существуют односторонние (конечные!) пределы , говорят, что функция имеет в разрыв первого рода (скачок); при разрыв называется устранимым. Если хотя бы один из этих пределов не существует (в частности, равен , разрыв называется разрывом второго рода.

Примеры:(1) - в 0 разрыв первого рода;(2) - разрывы в 0 второго рода.

4.3.Свойства функций, непрерывных на отрезке

Определение 4.3.Функция называется непрерывной на множестве (открытом), если она непрерывна в каждой точке этого множества. Функция называется непрерывной на замкнутом множестве ,если она непрерывна на внутренности этого множества и если .Для отрезка это означает, что и .То, что непрерывна на множестве , обозначается

Далее следуют утверждения, которые, с одной стороны, помогут в дальнейшем доказывать разные теоремы о более сложных объектах, а с другой стороны показывают, что естественное понятие непрерывности не противоречит математическому.

Теорема 4.3(1-ая Вейерштрасса).

Если , то она ограничена на (т.е., найдутся такие числа , что

Доказательство. Докажем, что существует .Если это не так, то ,такой что . Последовательность ограничена, следовательно у неё есть предельная точка .Пусть - подпоследовательность, сходящаяся к .В силу непрерывности функции , последовательность будет сходиться к .В силу выбора последовательности ,подпоследовательность бесконечнобольшая. Противоречие доказывает существование . Аналогично доказывается существование . Теорема доказана.

Теорема 4.4(2-ая Вейерштрасса). Если , то она достигает на максимума и минимума.

Доказательство. Докажем про максимум. Пусть . существует по Теореме 4.3.Докажем, что найдётся точка , для которой . Если это не так, то функция непрерывна на . По теореме 4.3, для некоторого . Тогда , что противоречит выбору .Противоречие доказывает теорему.

Теорема 4.5(1-ая Коши) Если ,то существует точка , для которой .

Доказательство. Пусть ,для определённости, Построим последовательность стягивающихся отрезков. Пусть ; поделим пополам, получим точку . Может быть два случая: либо ,и мы нашли точку ,в которой либо на концах одной из половин первоначального отрезка принимает значения разных знаков, обозначим левый конец этой половины правый - . В первом случае теорема для доказана, во втором будем делить пополам отрезок .Продолжая этот процесс, мы либо найдём точку , в которой , и в этом случае теорема будет доказана, либо получим последовательность стягивающихся отрезков, по длине стремящихся к нулю, и таких, что .Пусть - общая точка этих отрезков. Она принадлежит всем этим отрезкам, и , в частности, отрезку ; значит, она в точке непрерывна( если это внутренняя точка отрезка , то просто непрерывна; если это ,то непрерывна справа; если , то непрерывна слева). Рассмотрим .Согласно первому из этих равенств, , согласно второму - . Значит, , и теорема доказана.

Теорема 4.6(2-ая Коши). Если , то

Доказательство. Рассмотрим . Очевидно, . Положим .Теорема доказана.

Теорема 4.7(о существовании обратной функции). Пусть функция и строго монотонна. Тогда на однозначно определена функция , такая, что .

Доказательство.1.Определение .Пусть .Согласно 2-ой теореме Коши,.Такой только один. Равенство при противоречит строгой монотонности. Положим .

Этим уравнением функция определена однозначно на всём отрезке (Почему на всём?). 2. Непрерывность . Пусть, по-прежнему, и пусть целиком принадлежит .Такое заведомо существует, потому что - внутренняя точка отрезка .Пусть .Тогда .Мы по нашли ,такое, что при отображении -окрестность точки целиком отображается в -окрестность точки .Непрерывность на доказана .Непрерывность слева и справа в и (с одной стороны!) доказывается аналогично. Теорема доказана(позже мы докажем её ещё раз как следствие теоремы о неявной функции).

Определение 4.4.Функция называется равномерно-непрерывной на множестве , если ,такое, что, как только , будет выполняться неравенство.

Теорема 4.8(Кантора).Если ,то на равномерно-непрерывна.

Доказательство. Предположим, что это не так. Тогда существует некоторое , для которого при любой последовательности всегда найдётся пара точек , для которых и .Пусть - предельная точка последовательности .Чтобы не вводить дополнительные индексы,предположим,что .Тогда и (в силу условия) Но в этом случае ,что противоречит предположению .Теорема доказана

5.Дифференцируемые функции

Определение 5.1.Функция называется дифференцируемой в точке , если она определена в некоторой окрестности этой точки, и если её приращение в этой точке может быть записано в виде

,

где - константа, не зависящая от точки , а - бесконечномалая при .

Положим .Тогда определение дифференцируемости в точке можно записать в виде .Видно, что функция , дифференцируемая в точке , непрерывна в этой точке, поскольку при имеем . Поделим наше равенство на . Получим

Следовательно, Этот предел называется производной функции в точке и обозначается одним из следующих символов: или .Верно и обратное: если у функции в точке существует производная, то функция в этой точке дифференцируема. Действительно, если производная существует, то , где - б.м. при . Следовательно, , что и требовалось. Сформулируем доказанное как отдельную теорему.

Теорема 5.1. Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно, чтобы она имела там производную.

Определение 5.2.Дифференциалом функции в точке называется произведение .

Если - независимая переменная, полагают ; не зависит от точки .Дифференциал линейно зависит от . Его называют главной линейной частью приращения функции в точке .(Главной, потому что при оставшаяся часть приращения функции, равная стремится к 0 быстрее дифференциала).

Теорема 5.2. Пусть и дифференцируемы в точке . Тогда

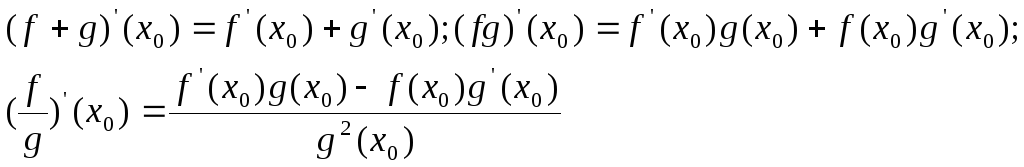
(Последняя формула верна при ).

Доказательство. Докажем последнее утверждение; остальные доказать ещё проще, а схема доказательства сохраняется. Имеем

.

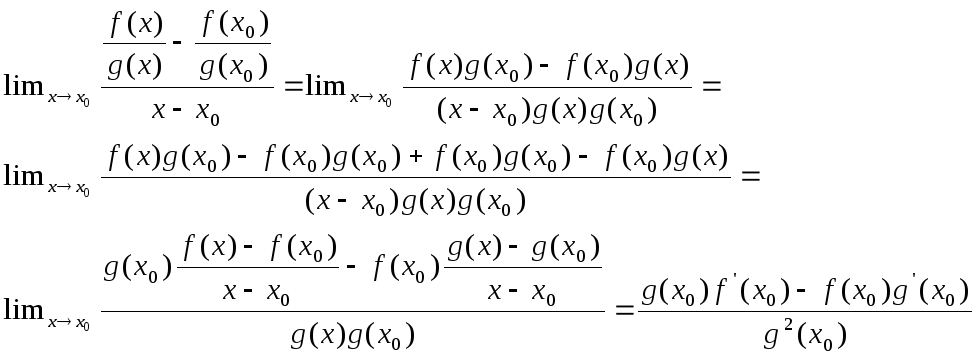Заметим, что мы имеем право писать в знаменателе, так как согласно с леммой о сохранении знака в некоторой окрестности точки , и можем переходить к пределу в сумме (в числителе) и дроби по свойствам функций, имеющих в предел.

Теорема доказана.

Теорема 5.2’.В условиях теоремы 5.2 имеем

Доказательство. Умножим равенства предыдущей теоремы на .

Теорема 5.3(о дифференцируемости сложной функции). Пусть определена в некоторой окрестности точки , , и дифференцируема в самой точке , а функция определена в окрестности точки , причём (а) ,,и(б) при . Тогда сложная функция, и .

Следует заметить, что и меняются в разных пространствах вещественных чисел!

Доказательство. Поскольку , имеем ,где - б.м. при. Аналогично, поскольку , имеем , где - б.м. при .Объединяя эти результаты, получим

При,так как . Значит выражение в скобках при является б.м.Теорема доказана.

Рассмотрим дифференциал функции в точке . По определению, он равен . Но .В этом случае , но всё равно имеем , т.е. дифференциал функции как функции от ищется по той же формуле, что и дифференциал функции как функции от .Это свойство называется инвариантностью формы первого дифференциала при замене переменной.

Теорема 5.3’.Первый дифференциал функции вычисляется по формуле независимо от того, будет независимой переменной или нет.

Это свойство очень важно при при вычислении интегралов. Оно не имеет места для дифференциалов высших порядков в общем случае.

6.Теоремы о дифференцируемых функциях.

Определение 6.1.Функция называется дифференцируемой на множестве ,если она дифференцируема .Это обозначается так:

Производная для в этом случае является функцией от . Если эта функция является дифференцируемой на , то её производная называется второй производной функции .Обозначение: . Вообще

Определение 6.2.Если , то, по определению, .Для в этом случае пишут .

Определение 6.3.Если , то .

Рассмотрим теперь вопрос об инвариантности .Если - независимая переменная, то - не зависит от , и (и вообще,).Если , то .Значит, если , инвариантности нет.

Теорема 6.1.Дифференциалы высших порядков не инвариантны, вообще говоря, относительно замены переменной.

Пусть функция определена на интервале . Точка называется точкой локального максимума функции , если существует окрестность , для всех точек которой .Точка называется точкой строгого локального максимума, если для всех точек окрестности .

Определение 6.5.При тех же условиях на функцию , точка называется точкой локального минимума функции , если для всех точек некоторой окрестности выполняется неравенство , и точкой строгого локального минимума , если последнее неравенство – строгое.

Определение 6.6.Точки локального максимума или минимума называются точками локального экстремума.

Теорема 6.2.(Ферма).Пусть функция определена и дифференцируема на интервале и - точка экстремума для . Тогда = 0.

Доказательство.Предположим для определённости, что - точка локального максимума. Пусть .Имеем

.Значит, . Пусть теперь .Рассматривая то же отношение, получим .Следовательно,. Теорема доказана.

Теорема 6.3 (Ролля). Пусть .Существует такая, что .

Доказательство.1.Если - константа, то , и теорема верна. 2.Если функция -не константа, то ,во всяком случае, она непрерывна на (поскольку дифференцируема).Но тогда она достигает где-то на своего максимума и минимума. Хотя бы одна из этих точек не будет совпадать ни с ,ни с , и потому расположена на .Значит, она будет точкой локального экстремума, и производная в ней будет равна нулю. Теорема доказана.

Теорема 6.4(Коши). Пусть . Тогда существует точка , для которой

.

Доказательство.1.Заметим, что , так как в противном случае по теореме Ролля нашлась бы точка , в которой .2. Для функции

на выполнены все условия теоремы Ролля. Найдётся по этой теореме точка , в которой .Имеем

; поделив на ,получим что требовалось доказать.

Следствие 6.4.1.(Теорема Лагранжа). Пусть .Существует , для которой

.

Доказательство. Достаточно взять в предыдущей теореме.

Следствие 6.4.2.(«Простое» правило Лопиталя). Пусть функции определены в проколотой(и может быть односторонней) окрестности точки и (1);(2) определены в той же окрестности, и (3);(4)пусть существует .Тогда .

Доказательство. Пусть.Функции удовлетворяют условиям теоремы Коши .Значит,

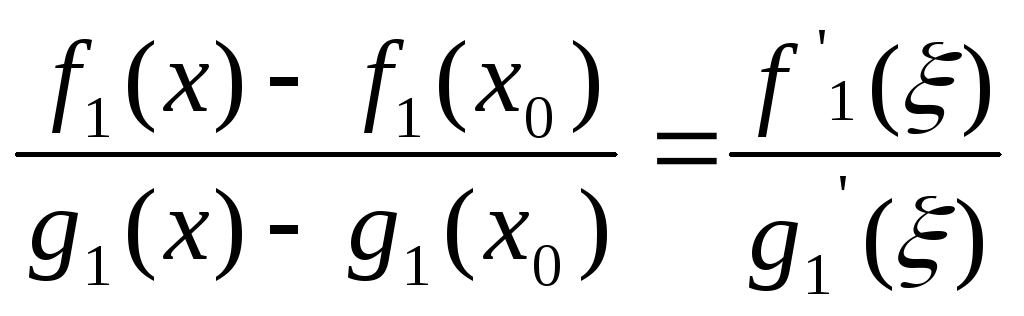для некоторой точки .При функции и совпадают, так что полученное равенство можно переписать как

. При имеем , теорема доказана.

Аналогичная теорема верна для неопределённости , но её мы пока доказывать не будем. Желающие могут найти её в 1-ом томе «толстого» Фихтенгольца.

Следствие 6.4.3(Формула Тэйлора с остаточным членом в форме Пеано).Пусть функция имеет производные всех порядков до ()-го включительно в некоторой окрестности и производную в самой точке . Тогда для

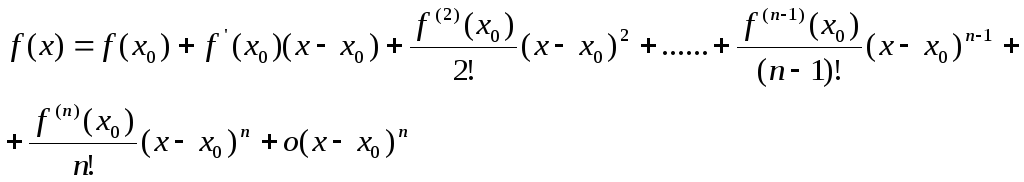
Доказательство. Вычислим предел:

(Легко видеть, что к данной дроби применимо правило Лопиталя. Применяя его () раз, получим)

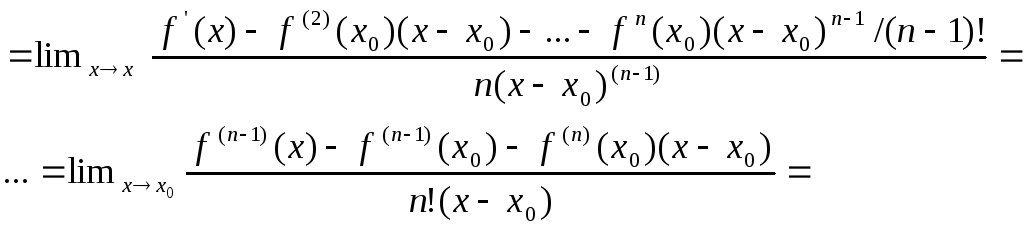
(Функция,значит ,где- б.м.;имеем: )

.

Теорема доказана.

Разность

называется остаточным членом формулы Тэйлора в форме Пеано. Ниже, при более жёстких ограничениях на функцию , мы получим форму остаточного члена, более удобную в приложениях.

6.5.Остаточный член в форме Шлёмильха – Роша и его варианты.

Пусть функция определена в некоторой окрестности точки и имеет там непрерывные производные порядков до включительно, и пусть в проколотой окрестности у неё есть конечная . Пусть - некоторая точка этой окрестности. Рассмотрим функцию

,.

Эта функция непрерывна на и имеет внутри него конечную производную. Кроме того, .Если вычислить производную в точке , получим

.

Пусть теперь - любая функция, для которой при .По теореме Коши, для имеем

,где или, что то же самое, , . Подставляя в эту формулу , после умножения на , получим

.

Полагая , получим

.

Такая форма остаточного члена называется формой Шлёмильха – Роша.

Если известны какие-нибудь ограничения на модуль производных независимо от их порядка, такая форма позволяет оценивать величину остаточного члена для конкретных

Особенно употребительны два частных случая. При получаем остаточный член в форме Лагранжа

.

При получаем остаточный член в форме Коши

.

Полученные формы остаточного члена позволяют более точно оценивать разность , если известно ,например, что модуль производной ограничен какой-либо константой.

Теорема 6.6.Если функция, то обратная функция

Доказательство. При рассмотрении непрерывных функций было доказано, что если на отрезке задана строго монотонная функция, то на области её значений определена однозначно обратная к ней функция, которая будет строго монотонной и непрерывной. Из условий теоремы 6.6 следует, что строго монотонна. Поэтому существование и непрерывность доказывать не нужно. Имеем

.

Здесь, очевидно, имеется в виду, что .Теорема доказана.

Она позволяет не вычислять отдельно производные обратных функций, если производные прямых функций известны.

7. Выпуклые функции

Мы будем рассматривать функции, заданные на промежутках числовой оси. Пусть - такой промежуток.

Определение 7.1.Функция называется выпуклой на множестве , если для любого и для любых точек имеет место неравенство

.

Эквивалентное определение: выпуклая, если для любых и любых , таких, что выполняется неравенство

.

Функция называется строго выпуклой, если для всех выполняется строгое неравенство. Функция называется вогнутой, если неравенство выполняется с противоположным знаком.

Понятно, что если - выпуклая, то - вогнутая (и наоборот).

Геометрически функция является выпуклой, если хорда, соединяющая любые две точки её графика, лежит выше самого графика. Будем считать в дальнейшем .

Полагая , получим

Последнее неравенство эквивалентно такому

,

в чём легко убедиться, освободившись в них от знаменателей. Это неравенство назовём основным.

Геометрически основное неравенство показывает, что при тангенс угла наклона хорды слева (от к всегда не превосходит тангенса угла наклона хорды справа (от к ); иными словами, тангенс угла наклона хорды не убывает при движении от точки к точке .

Теорема 7.1.Если - выпуклая функция на промежутке и - внутренняя точка , то (конечные!).

Доказательство. В неравенстве

устремим . Поскольку левая часть не убывает и ограничена, у неё есть предел, который по определению совпадает с . Аналогично, устремив в том же неравенстве, получим, что .

Теорема доказана.

Следствие 7.1. Выпуклая функция непрерывна в любой внутренней точке области определения.

Действительно, из существования правой и левой производных следует, что и при .

Теорема 7.2.Для того, чтобы дифференцируемая функция была выпуклой на промежутке , необходимо и достаточно, чтобы её первая производная не убывала.

Доказательство. Если функция выпуклая, то устремляя в основном неравенстве сначала к , а потом к , получим .

Наоборот, если выполнено неравенство , пусть .Если на всём производная равна константе, то основное неравенство выполняется. Если производные не равны, то ,по теореме Лагранжа, имеем

, где . По предположению,, и мы получили основное неравенство. Теорема доказана.

Теорема 7.3. Для того, чтобы функция была строго выпуклой на промежутке, достаточно, чтобы её производная строго возрастала.

Для доказательства следует только обратить внимание на то, что в предыдущем доказательстве, в условиях теоремы 7.2, всегда будет .

Теорема 7.4. Для того, чтобы дважды дифференцируемая на промежутке функция была выпуклой, необходимо и достаточно, чтобы её вторая производная была неотрицательной.

Очевидно, так как условие означает, что производная первая не убывает.

Теорема 7.5.Для того, чтобы дважды дифференцируемая функция была строго выпуклой, достаточно, чтобы её вторая производная была положительной.

В этом случае первая производная строго возрастает.

Теорема 7.6. Для того, чтобы функция была выпуклой, необходимо и достаточно, чтобы в любой точке её график лежал не ниже касательной.

Доказательство. Если функция в точке лежит выше касательной, то имеет место неравенство

.Если , оно означает, что , если , неравенство будет в обратную сторону. То есть, для любых будет

- основное неравенство. Значит, функция выпуклая.

Наоборот, если функция выпуклая, то для любых выполняется неравенство

, которое эквивалентно утверждению, что функция лежит выше касательной. Теорема доказана.

8. Дополнительные сведения о свойствах дифференцируемых функций

Теорема 8.1. (Дарбу). Пусть . Если , то , для которой .

Доказательство. Положим . Тогда . Пусть, для определённости, . Тогда правее точки убывает, левее точки - возрастает. Значит, минимум функции достигается внутри интервала в некоторой точке . Очевидно, функция дифференцируема в точке и некоторой её окрестности. Следовательно, и теорема доказана.

Таким образом, для производных верен аналог теоремы Коши для непрерывных функций.

Рассмотрим теперь вопрос о непрерывности прозводной.

Из теоремы Лагранжа следует, что если . Пусть при этих предположениях . Тогда

. Пусть .Тогда .Выражение слева будет стремиться к , и предел правого выражения тоже будет равен . Однако предел может при этом существовать, в этом случае производная будет непрерывна в точке .Но он может и не существовать, как показывает пример функции .Таким образом, верна

Теорема 8.2. (о разрывах производных). Если функция , то в любой точке этого интервала её производная либо непрерывна, либо имеет разрыв второго рода (в разных точках по-разному).

Второй семестр

ИНТЕГРАЛЫ

1.Неопределённый интеграл и первообразная

Определение 1.1. Пусть функция определена на отрезке .Функция называется первообразной для функции на отрезке , если . Вместо отрезка можно взять любой промежуток .

Пусть - первообразная для на . Тогда и , будет первообразной для на том же отрезке.

Пусть теперь - две любых первообразных для на отрезке .Тогда

.Как следует из теоремы Лагранжа, это означает, что , где - некоторая фиксированная для всего отрезка константа.

Мы только что доказали, что

Теорема 1.1 Для того, чтобы две функции были первообразными для одной функции на отрезке , необходимо и достаточно, чтобы они различались на константу.

Определение 1.2. Совокупность всех первообразных функции на отрезке называется неопределённым интегралом функции на отрезке и обозначается .

Если - какая-нибудь первообразная для , то где - произвольная константа.

2.Свойства неопределённых интегралов.

Все свойства неопределённых интегралов вытекают из определения. Для их проверки (или доказательства) достаточно продифференцировать правую и левую части соответствующего равенства; если результаты совпадут, равенство верное.

2.1., если интегралы справа существуют;

2.2. , где - произвольная постоянная; если , то

и

2.3.(Замена переменной) Если , то

2.4. (Правило интегрирования по частям) , если ;

2.5. Стандартная таблица простейших неопределённых интегралов:

1.,если ;

2.

3.

4.

5.

6.

7.

8.

3. Можно заметить, что в стандартную таблицу не попали некоторые интегралы от простейших элементарных функций. Это произошло по двум причинам.

Во-первых, интегралы от логарифма, тангенса, котангенса, арксинуса, арккосинуса, арктангенса и арккотангенса легко вычисляются через приведённые. Во-вторых, в простейших случаях интеграл , где - простейшие элементарные функции

не выражается в конечном виде через простейшие элементарные функции(например,

).

Когда приходится вычислять (говорят: брать) интеграл от функции, которую Вы видите в первый раз, не факт, что Вам удастся подобрать такую конечную комбинацию элементарных функций, производной которой является подинтегральная функция.

Обычно, если сразу не видно, как свести предложенный интеграл к табличному, нужно попытаться упростить его, либо разбив на сумму более простых, либо испробовав какую-либо замену переменных. Часто встречающимися в задачниках заменами являются такие:

и так далее. Нужно помнить, что вместе с следует через новую переменную заменять и .Известно несколько типов интегралов,

которые всегда выражаются в конечном виде через элементарные функции. Некоторые из них приведены ниже.

3.1. Рациональные дроби от одной переменной.

Так называются дроби вида

, где числитель – многочлен степени от , знаменатель – многочлен степени от . Нас будет интересовать случай . Если это неравенство не выполняется, можно разделить числитель на знаменатель с остатком. Для остатка это неравенство будет выполняться.

По одной из основных теорем алгебры, всякий многочлен от одной переменной с действительными коэффициентами может быть однозначно разложен в произведение

, где все коэффициенты - действительные числа, - все действительные корни этого многочлена, каждый со своей кратностью , а все квадратные трёхчлены не имеют действительных корней.

Для доказательства возможности выражения неопределённого интеграла от рациональной дроби в конечном виде через элементарные функции имеют значение следующие три факта. (1)Всякую правильную(с ) рациональную дробь можно разложить на простейшие; (2) Каждой скобке вида при этом разложении соответствует набор дробей

, а каждой скобке вида - набор дробей ; (3)Интеграл от дроби сводится к сумме рациональной дроби с интегралом от .

(Подробности можно посмотреть в «толстом» Фихтенгольце).Таким образом , интеграл от всякой рациональной дроби может быть выражен в виде суммы рациональной функции, логарифмов и арктангенсов в конечном числе.

3.2. Всякая рациональная функция от тригонометрических функций может быть приведена к обычной рациональной заменой ; при замене в интеграле , .

3.3.Рациональную функцию от можно свести к обычной рациональной одной из замен Эйлера.

(1).Если , можно сделать замену ; тогда , и выражается через рационально.

(2). Если , положим .

(3). Если подкоренное выражение имеет различные действительные корни , положим

.

4. Вопросами о том, что делать, если интеграл не выражается в конечном виде через элементарные функции, мы заниматься не будем.

Определённый интеграл

1. Мы будем рассматривать функции, определённые на отрезке . Разбиением отрезка называется выбор точек .(Неравенства могут быть в другую сторону, но все сразу). Мелкостью разбиения называется . Интегральной суммой для данного разбиения называется сумма вида

Определение 2.1. Определённым интегралом называется, если он существует, .Если определённый интеграл существует, функция называется интегрируемой по Риману на отрезке .

Отметим, что в определении не говорится ничего о выборе точек ; их можно выбирать любым способам, лишь бы . То есть, никакие конкретные суммы при взятии предела не рассматриваются, ибо при любом фиксированном таких сумм бесконечно много. Тем не менее, рассмотрение интегральных сумм иногда полезно.

Следствие 1.1. Функция интегрируема, и .

Действительно, для любого разбиения и любого выбора точек интегральная сумма равна .

Теорема 2.1. Если функция интегрируема на отрезке то она на нём ограничена.

Доказательство. Предположим, что не ограничена в точке .При любом , можно выбирать точки так, чтобы: 1)произведение для отрезка , на котором лежит точка , было сколь угодно большим по модулю; 2) чтобы остающаяся часть интегральной суммы была по модулю меньше половины модуля указанного произведения. Если функция интегрируема, у таких интегральных сумм должен быть конечный предел, что противоречит принципу их построения. Теорема доказана.

В дальнейшем мы будем рассматривать только ограниченные на отрезке функции.

Теорема 2.2.Если функция на отрезке интегрируема и не отрицательна, то интеграл от неё не меньше нуля.

Доказательство. Любая интегральная сумма будет неотрицательной, значит и предел этих сумм неотрицателен.

Теорема 2.3.Если на отрезке и обе функции интегрируемы, то

.

Очевидное следствие из предыдущего утверждения.(Применить предыдущую теорему к )

Теорема 2.4. Множество интегрируемых на отрезке функций образует линейное пространство.

Достаточно сравнить интегральные суммы.

Теорема 2.5. .

Очевидно из определения интегральной суммы.

Теорема 2.6.Если , то

Доказательство – из свойств модуля и интегральных сумм

С точки зрения Теорем 2.5,2.6, естественно положить по определению

,

если на некотором отрезке функция интегрируема.

Суммы Дарбу.

Будем для удобства считать, что .

Определение 2.2.Пусть есть некоторое разбиение отрезка . Пусть ; положим

.

Эти суммы называются нижней и верхней суммами Дарбу. В наших предположениях, всегда . Суммы Дарбу зависят только от разбиения отрезка и не зависят от выбора точек .

Теорема 2.7.При добавлении к данному разбиению одной точки нижняя сумма может только увеличиться, верхняя – только уменьшиться.

Доказательство. Пусть - новая точка разбиения, и пусть она лежит на отрезке разбиения . Ни на одном из вновь образовавшихся отрезков нижняя грань функции не может стать меньше, а верхняя – не может стать больше, чем на исходном отрезке. Теорема доказана.

Теорема 2.8. Для любых двух разбиений нижняя сумма первого (второго) не может превосходить верхнюю сумму второго(первого).

Доказательство. Рассмотрим третье разбиение, которое получается, если объединить точки первого и второго разбиений. Нижняя сумма для третьего будет не меньше, чем для первого, верхняя для третьего будет не меньше, чем нижняя для третьего и не больше, чем верхняя для второго, согласно предыдущей теореме. Теорема доказана.

Теорема 2.9.Существуют

.

Доказательство. По предыдущей теореме, множество нижних сумм ограничено сверху, а множество верхних сумм – снизу. Значит, у этих множеств есть, соответственно, верхняя и нижняя грани. Взятие пределов предполагает добавление точек разбиения, при котором нижние суммы не убывают, верхние не возрастают. Значит, предел нижних сумм будет существовать и совпадать с верхней гранью, а для верхних сумм – совпадать с нижней гранью. Неравенство из условия теоремы получится, если перейти к пределу в неравенстве . Теорема доказана.

Теорема 2.10. (Критерий интегрируемости) Для того, чтобы функция была интегрируема на отрезке , необходимо и достаточно, чтобы .

Доказательство. Достаточность. Если условие теоремы выполнено, то .Для любого , и для любого выбора точек имеет место неравенство . Следовательно, предел интегральных сумм существует и равен .

Необходимость. Если интеграл существует, то , такое , что для всех интегральных сумм с мелкостью меньше будет выполняться система неравенств.Перейдём сначала в левом неравенстве к верхней грани, потом в правом – к нижней. Получим ; то есть, разница . Поскольку произвольно, теорема доказана.

Определение 2.3. называется колебанием функции на отрезке .

Критерий интегрируемости функции на отрезке эквивалентен требованию

.